基于不同故障类型的不完全预防维护模型

曲玉祥，吴 更生

(清华大学 工业工程系，北京 100084)

1 概述

维护 (或维修) 是使系统或设备维持在可用状态或恢复故障缺陷的所有活动。如果维修可以使系统修复达到全新的状况，称为完全维护；现实中大部分系统很难通过维修活动达到全新的状况，即不完全维护，如对机车发动机进行定期检修，可以在极大程度上改善发动机的工作状况，却难以达到全新的效果。不完全维护是使系统的失效率恢复程度介于完全维护和最小修复之间，系统状态介于“全新”和“如旧”状态之间的维护活动[1-2]。目前，描述不完全维护对系统失效率的改善程度是研究不完全维护的一个关键性问题[2-6]。

Malik[2]在维修排序问题中引入改善因子的概念描述维修后系统失效率的改进程度。Lie 和 Chun[3]给出了维修费用与系统工龄函数关系的一系列曲线描述改善因子。Suresh 和 Chaudhuri[4]利用改善因子找出系统维修 后的初始状态。Jayabalan和Chaudhui[5]利用常数的改善因子，通过分支演算法求解维修时间。Pham和Wang[6]将不完全维护的处理方法系统地归纳为8种类型。Martorell等[7]提出了工龄比例恢复和工龄比例减少两种不同模型描述设备经过维护变“年轻”的效果。

构建不完全维护模型通过将维护对象视为单一部件系统，针对具有耗损特性的设备，考虑失效限度，实施周期预防维护策略；假设维护时间间隔为τ，通过单位时间维护成本最小化确定具体的维护策略。维护间隔内发生故障包含两种类型，即Type I 和Type II[8](简称 I 型故障和 II 型故障)。I 型故障指系统故障可修，并进行最小修复，假设最小修复不改变设备的可靠度和失效率。II 型故障是指系统故障严重以至不得不更换全新部件甚至厂修的情况，此时最小修复无效，设备需要更换或进厂维修；执行一定次数的预防维护后进行预防更换。以铁路机车故障维修为例，主要为机故 (机故是指机车在牵引中出现故障，申请到下一站侧线进行修理，修理时间超过 30 min，机故不影响其他列车行驶) 导致的临修和机破 (机破指机车在牵引过程中出现了难以修复的故障并且不能继续前行) 导致的临修或段修，此类维修以排除故障使机车恢复正常运行状态为目标，对机车既有寿命及失效率产生的影响很小，视为最小修复。

不完全维护模型的基本假设包括每次投入的预防维护成本Cpm、预防更换成本Cpr及最小修复成本Cmr为常数，预防维护成本及最小修复成本不大于预防更换成本。相比设备正常运行时间，预防维护、最小修复及预防更换所需时间可以忽略不计。改善因子受设备有效工龄、预防维护成本率等因素影响，忽略环境条件、操作条件及人为操作不当等因素。

2 耗损型设备不完全维护模型的构建

2.1 改善因子

参考维护活动改善效应的相关研究，应用改善因子ηi，受设备工龄和预防维护成本率 (预防维护成本Cpm与预防更换成本Cpr的比值) 的影响。取值范围0≤ηi≤1，当ηi=0 时表示最小修复，ηi=1代表完全维护，具体表达式如下。

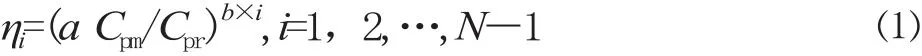
2.2 有效工龄和可靠度

考虑维护活动的工龄恢复效应，由改善因子确定设备维护后的状态，即设备的有效工龄，计算可靠度等指标。由公式(1)可知，若预防维护成本Cpm与预防更换成本Cpr的比值越大，改善因子越大，恢复效果越好，有效工龄越小。采用工龄比例减少模型，即只有前一次维护后的工龄可以得到比例恢复，则设备在第i次维护前后的有效工龄分别如公式(2)、公式(3)所示。

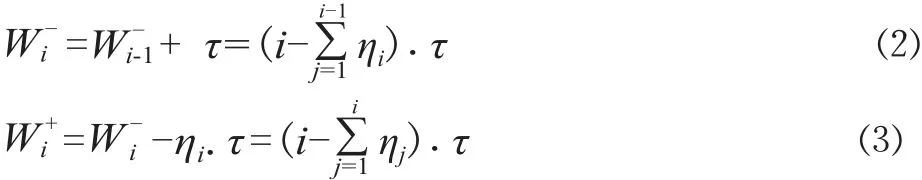
式中：τ为设备预防维护时间间隔；W-i、分别为设备在第i次维护前、后的有效工龄。

随着维修次数的增加，即i的增加，改善因子减小，即随着时间的增加，即使投入相同的预防维护成本，对系统的改善也会变差。设备执行完N－1 次预防维护后，在第N次进行预防更换，可以得到预防更换的时间点。

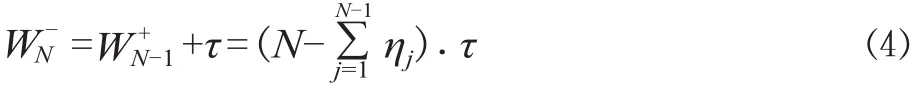
相应时间点的可靠度由设备的可靠度函数R(t)求出：

2.3 维护成本函数

假设设备使用期限为无限时间域时，以单位时间期望成本作为维护优化的目标函数。考虑2种故障类型[6]，假设系统发生 I 型故障的概率为1－θ，此时系统可以进行最小修复；当系统以概率θ发生 II 型故障时，最小修复无效，系统进行更换。鉴于我国目前的检修现状，考虑失效限度成本率最小化的预防维护模型。这种预防维护模型的成本函数包含3个部分：预防维护成本、最小修复成本和预防更换成本。期望总成本TC的表达式为：

式中：pi表示第i次发生故障的概率。

确定设备的寿命分布是进行维修决策的一个重要前提，由于威布尔分布具有较强的适应性和工程意义，在可靠性工程中被广泛应用，能够较好描述具有耗损特型的机械设备的寿命分布。假设系统的寿命分布为二参数威布尔分布，其失效率函数为：

式中：α为尺度参数，也称为特征寿命，当可靠度R=e－1=0.368 时的寿命，用以描述产品达到的总体寿命水平；β为形状参数，数值的大小决定失效率曲线的形状。当β=1 时，威布尔分布简化为指数分布，失效率是与时间无关的常数；β＞2 时，失效率函数是单调递增的凸函数，即耗损型部件所具备的失效率特征。

问题在哪里，监督就要跟进到哪里。“奇葩”案例的背后是违纪违法问题呈现出的新特点，我们要准确把握，加强监督，对症下药。

当系统的预防维护时间间隔为τ，则单位时间期望维护成本最小化的目标函数为：

2.4 模型的其他约束条件及求解

以维护时间间隔τ和预防更换点N为决策变量，在单位时间期望成本最小的目标下，求取τ和N的最优解：

在此基础上，为了满足系统运行的需要，可以预先设定可靠度水平Rmin，当系统可靠度等于此限制时，执行预防更换动作。若为设备预防更换时间点，则要求：

由系统的失效率函数，即可得到最优维护间隔，利用 Matlab 对模型编程求解。

3 数值验证与分析

对模型进行数值验证，确认2种预防维护模型的求解方法是可行的。为此，需要给定部件失效模式、维护成本等相关参数，如表1所示。

表 1 用于验证模型的相关参数

3.1 成本率曲线、预防更换时间及最优化维修策略

假设模型中的可靠度限制水平Rmin=0.6 和Rmin=e－1=0.368，取发生 II 型故障的概率为θ= 0.1，另有预防更换的寿命为T=Nτ。通过计算，可以得到在不同可靠度要求下的成本率曲线和系统的预防更换寿命曲线，如图1所示。

从图 1a 中可以看出：系统预防更换的寿命会随着总预防维护次数的增加而先增加后降低，也就是系统的预防更换寿命存在极值点，极值点对应最优维护成本率时的预防维修次数。此外，预先设定的可靠性水平越高，则系统越容易被淘汰，即相同条件下，预防更换的寿命相对较短。

图 1b 表示了不同的可靠度要求时，系统预防维护成本率随着总预防维修次数的变化曲线。系统的维护成本率存在极值点。当Rmin=0.6 时，最优维护次数为 25，其所对应的预防维护成本率为 0.436万元；当Rmin=0.368 时，最优维护次数为 24，所对应的预防维护成本率为 0.407 万元。较高的可靠度限制水平对应较高的预防维护成本，表明了成本率对可靠度的敏感度关系。

图 1 系统的预防更换寿命及维护成本率随预防维修次数的变化曲线

模型考虑了失效限度使得系统在运行和维护过程中具有较好的可靠性能，更符合实际应用的需要，设定可靠度限制水平Rmin对系统的不完全维护策略具有重要意义。因此，在制定设备维护方案时，决策者需要对设备可靠运行的需求进行综合考虑，在可靠度限制水平与维护成本间找到一个平衡点。

3.2 II型故障对成本率曲线的影响

模型中考虑了2种故障类型，即存在 Type II 故障类型，它的发生几率θ对成本率也具有较大的影响。在不同θ的情况下，预防维护成本率的变化，如图2所示。

由图2中可以看出，θ的增加会降低系统预防维护的成本。一般情况下，发生II型故障，必须更换新的器件，最小修复不再起作用，维护终止，维护成本整体会降低。随着θ的增加，系统维护成本率最小值所对应的最佳维修次数随之增加，即系统需要进行更加频繁的预防维护。

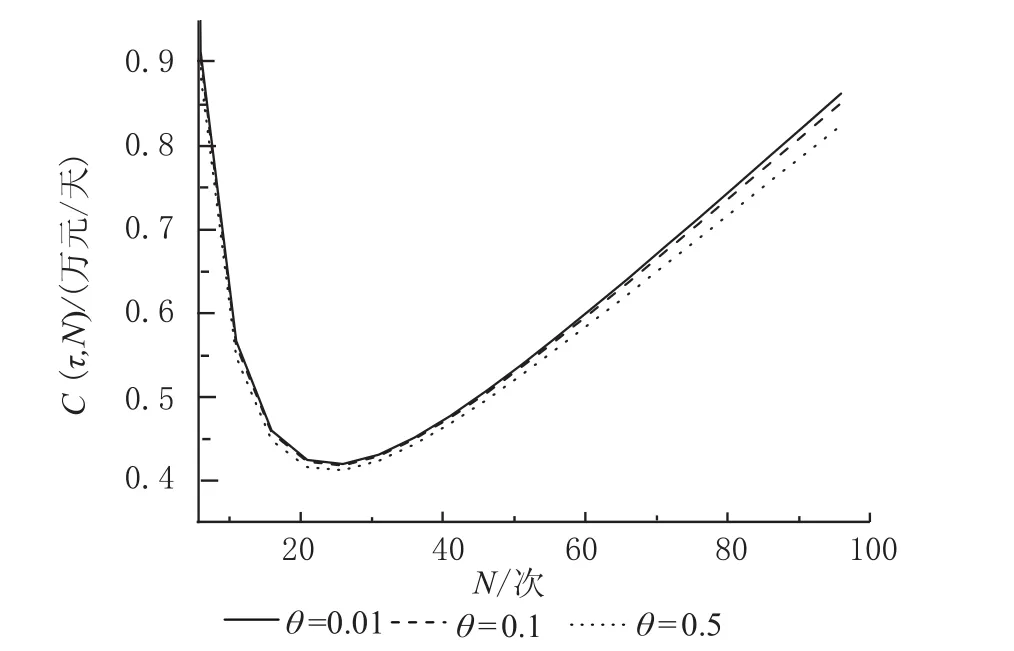
图 2 不同的II型故障发生率情况下的成本率随预防维护次数变化曲线 (Rmin=0.368)

3.3 威布尔参数的敏感度分析

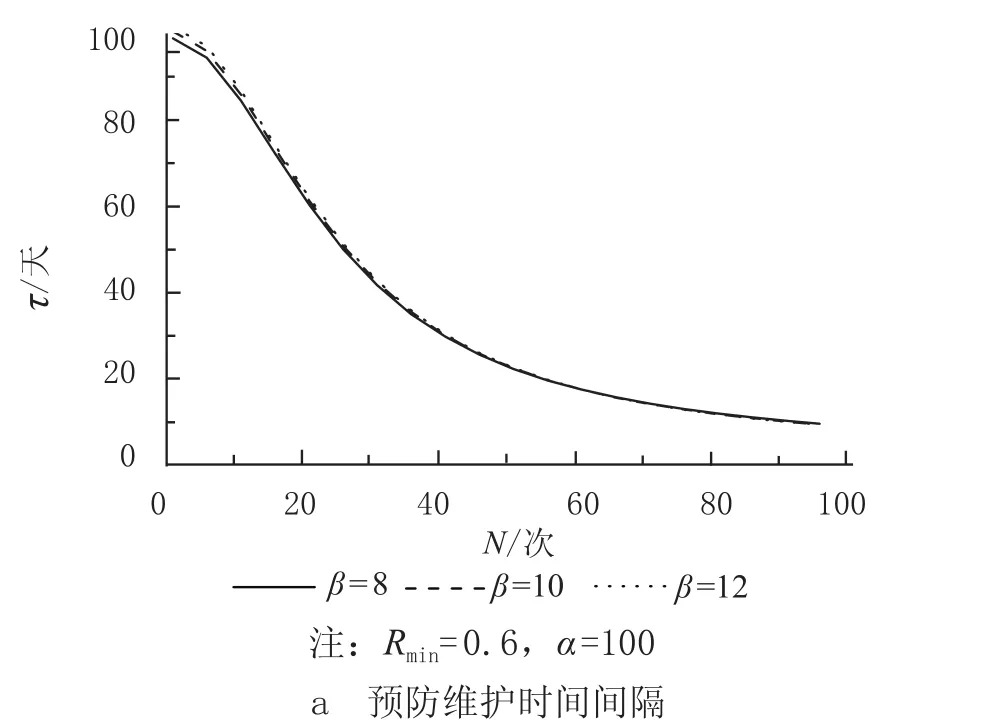
对部件的威布尔分布参数进行敏感度分析中，形状参数β是最重要的参数，决定了威布尔分布的形状和变化趋势。只改变形状参数β，表1中的其他参数保持不变，对模型进行求解优化。从图3中可以看出，当单位时间成本C(τ，N) 最小时，β越大，模型的维护时间间隔τ和预防更换点N越小，维护成本率因总时间T的缩减而增加，更换点的可靠度水平因T的缩减而增加，总体上都比较低。β较小时，τ、N以及维护成本率受β的影响较为显著。

按照类似的方法对尺度参数α进行敏感度分析，只改变尺度参数α，其他参数保持不变。从图4可以看出，模型维护时间间隔都随着α的增加而增加，维护成本率则相应地减小。

图 3 不同 β 条件下预防维护时间间隔及成本率随预防维护次数的变化

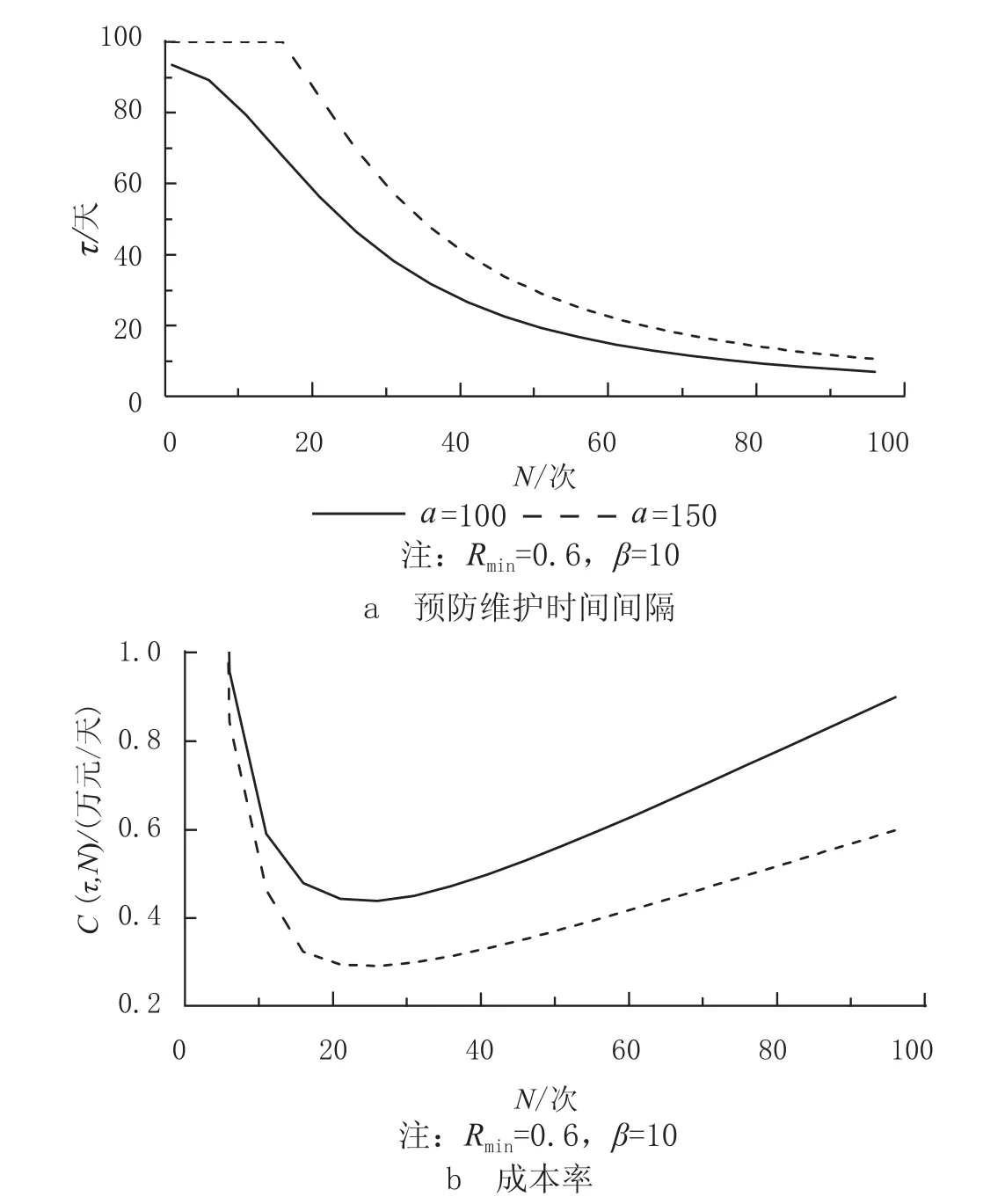
图 4 不同 α 条件下预防维护时间间隔及成本率随预防维护次数的变化

4 结束语

通过引入受维修次数、预防维护费用共同制约的改善因子，全面考虑两种不同的故障类型，建立不完全维护模型，以寿命期内的最小维护成本率为目标，求解相应系统装备的维修策略，即最佳的预防维修时间间隔以及最佳的预防维修次数。模型假设部件寿命服从威布尔分布，引入第二种故障类型发生概率为θ的假设，给出成本率的解析表达式。可以预先设定系统可靠度的最低值，实现不同可靠度条件下的系统最优维护方案。

通过设定不同的参数β、θ等，分析成本率曲线、时间间隔，以及系统寿命对不同参数的敏感度，并且对各种参数对系统最佳维修次数的影响进行了详细的分析。模型重点考虑单部件耗损型设备，对于其他类装备的不完全维修策略也具有一定的参考价值。

[1] Wireman T. World class maintenance management[M]. New York：Industrial Press，1990.

[2] Malik V，Jardine A K S. Optimal replacement for a general model with imperfect repair[J]. Journal of the Operational Research Society，1992，43 (2)：111-120.

[3] Lie C H，Chun Y H. An algorithm for preventive maintenance policy[J]. IEEE Transactions on Reliability，1986，35(1)：71-75.

[4] Sruesh P V，Chaudhuri D. Preventive maintenance scheduling for a system with assured reliability using fuzzy set theory[J].International Journal of Reliability，Quality and Safety Engineering，1994，1(4)：497-513.

[5] Jayabalan V，Chaudhuri D. Optimal maintenance replacement policy under imperfect maintenance[J]. Reliability Engineering and System Safety，1992(36)：l65-l69.

[6] Pham H，Wang H. Imperfect maintenance[J]. European Journal of Operational Research，1996，94(11)：425-437.

[7] Martorell S，Sanchez A and Vicente Serradell. Age-dependent reliability model considering effects of maintenance and working conditions[J]. Reliability Engineering and System Safety，1999，64(1)：19-31.

[8] Sheu S H，Chen J A. Optimal lot-sizing problem with imperfect maintenance and imperfect production[J]. International Journal of System Science 2004，35(1)：69-77.