巧用作业，培养学习兴趣

■江苏省无锡市山明中学 丁 洁

传统的数学作业形式呆板单调，容易让学生产生厌烦情绪，从而导致部分学生反感数学。基于此，凸显新课程标准，作业模式应关注学生个体差异性，强调情景性、可操作性，在作业中培养兴趣，发展数学思维能力。以下对于作业布置谈谈个人见解。

一、作业的布置

1.作业的基础布置，引导学生体验学习的满足感。由于很多教师在布置作业时采取“一刀切”的模式，导致了部分学困生根本无法消化知识，在作业中不断遭受的挫败感，直接导致了他们学习数学兴趣的丧失。所以，作为教师，我们的首要任务就是要帮助学生体验学习中的成就感，“让人人都能学数学”。于是我的第一层作业是顾及全班每一个学生的，即“讲什么内容做什么题”。

例1.苏科版八年级的《勾股定理》：

①消防车救火，若消防车能开至离住宅15米处，车内配备32米的云梯，试问，消防车可以救出多高处的被困人群？

②若消防车高2米，试问可救出多高处的被困人群？

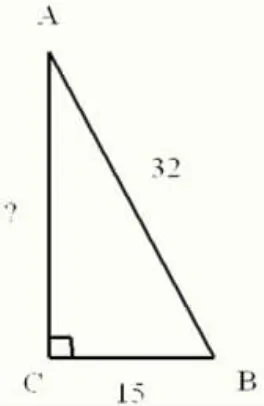
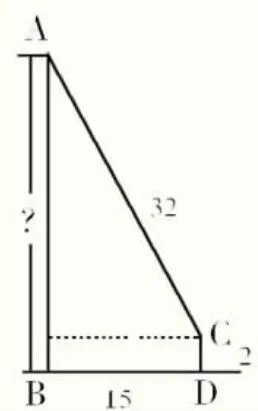
分析：第一小题比较简单，是对勾股定理的巩固，这样一来可以强化学困生对基础知识点的理解，二来可逐步建立起他们学习数学的自信心。第二小题仅仅是在第一题的基础上增加了一个图形的分割，在题目的简单变形中让学生感知趣味，进而激发其求知欲，让其体验学习中的满足感。

2.作业的提高布置，引导学生挖掘思考中的乐趣。在简单巩固了知识点以后，接下来当然是要喂饱“中上游”的学生，所以我接下来的作业会提高难度。同时为避免学生产生所谓的畏难情绪，我会在提问上进行分层设定，让学生在循序渐进中感受思考的乐趣，同时让“不同的学生学到不同的数学”。

例2：苏科版七年级下册中的动点问题：

直角梯形 ABCD中，AD∥BC，∠B=90°，AD=24cm,AB=20cm,BC=28cm，动点P从A以1cm/s速度出发向D点运动，动点Q从C点出发以2cm/s速度向B点出发，已知两动点同时出发，问：①过多少秒后，四边形PQCD成平行四边形？②过多少秒后，四边形PQCD成直角梯形？③过多少秒后，四边形PQCD的面积是梯形ABCD面积的一半？

分析：整道题中问题的设置是相互衔接的，第一小问是铺垫，主要是巩固四边形中动点问题的一般处理，根据性质“一组对边平行且相等的四边形是平行四边形”来列出等量关系PD=CQ；第二小问难度提升，但沿用第一小问的思路仍建立等量，只是此时的等量需建在与之相邻的矩形ABQP上；第三小问，难度更大，但思考中不难发现，第二小问其实给了暗示，四边形PQCD不管形状如何改变，它都是一个梯形，利用梯形面积求法，问题也就迎刃而解。

整道题目的问题设定是环环相扣的，前一题的做题思路为下一题做铺垫，学生在做题时可以先从常规题下手，然后不断往深层思考，在做题中挖掘探知的乐趣、思考的乐趣。

3.作业的深度布置，引导学生形成发散思维。当学生从不断的思考中逐步形成一定的逻辑思维能力时，说明其思维已具有一定的流畅性，此时我便开始进行思维的变通训练。每周我都会让学生做一次专题性作业，把相似的题目归为一类，做作业的同时把有关知识进行总结归纳，寻求知识间的内在联系，形成知识网络体系。掌握方法后，学生便可以“以不变的方法来应对万变的题目”。

例3.苏科版七年级下册《图形的全等》：

①已知△ABC、△BDE为等边三角形，证明AD=BD+CD。

②已知△ABC为等边三角形，∠BDC=120°，证明AD=BD+CD。

分析：这两道题的共性之处都是建立在图形全等判定的基础上，利用全等进行线段的等量转移，让线段转移到同一直线上，从而进行加减运算，这是推理的起点；而其各小题所存在的个性是条件的变换，让学生从起点开始推理，顺着其不同的条件，诱导出不同的结果。

例3①中，由条件中的等边三角形可得到一系列边与角的等量，不难证出△ABE≌△CBD，则CD转移至AE，加之BD=DE，从而得解。而②中变换了条件，关键就是如何用好“120°”。沿用第一题的思路，要制造全等，而全等的证明需要边或角之间的等量关系。于是反向延长DC，使DE=BD，制造等边，从而出现等量以证明△ABD≌△CBE。

我始终相信数学题是做不完的，我们要从有限的题目中学会思考的方法，由此便可以举一反三，以一当十。

二、错题的评讲

对于学生作业中出现的形形色色的问题，大多数的教师采取直接将答案告诉给学生的方法，虽然这样可以节省评讲时间，但不久便发现，学生依旧我行我素，于是出现了教师一再讲、学生一再错的情况，这也让众多教师感到头疼。

其实作业的评讲特别是针对错题的评讲实际是一种特殊的复习，因为针对学生错误点及薄弱环节的总结和归纳，更能有效地提高学生的学习成绩及能力。因此我着重将评讲分为成因分析、纠正错误、拓展思维提高能力三部分。

1.成因分析。当教师问学生为什么出错时，可能听到最多的回答是“我太粗心了”，可就是这所谓的“粗心”导致类似的错误一再地发生。看来粗心并非是缘由。如果将作业中错误的成因进行深究，你会发现学生的很多错误都可追溯到对知识点的含糊理解，所以要从根本上纠正错误，还是得解决学生本质上的问题，帮其强化对知识点的理解，细化概念的理解。

例 4.苏科版七年级下《幂的运算》：（-3）2与 -32

分析：学生容易将两者混淆。分清二者，首先应搞清什么是“幂”。前者底数为-3，表示-3的2次方，等于（-3）×（-3）；后者的底数是3，表示3的2次方的相反数，等于-3×3。从而从幂的概念上分清二者。

2.纠正错误。

例5：已知关于x的方程（3k+1）x2-2x-1=0有两个不相等的实数根，求k的取值范围。

一般学生认为两个不相等的实数解只须满足判别式大于0即可，没有发现其中的一个隐藏条件，这时教师就应该鼓励学生挖掘其中的隐藏条件。适当时可以予以提示，譬如：带有根号的代数式需要满足什么条件，二次方程需要满足何种条件。这样一来可以巩固学生前面学过的知识，二来培养学生数学思维的严谨性，今后碰到类似的问题，学生也可以考虑得比较周全。

关于这类易错易混的知识，要激励学生积极参与分析，当学生解题错误时，教师不要急于作出评价，要充分暴露学生错误产生的思维过程，利用学生的错误答案，引导他们进行验证，让他们自己发现矛盾，从而加深对知识的理解。同时，教师应当根据学生的反馈信息，反思“为什么会出现这样的问题”，应该如何调整教学计划，采取有效的策略和措施，从而顺着学生的思路组织教学，确保教学过程沿着最佳的轨道运行。

3.拓展思维，提高能力。如果教师在评讲错题时，仅仅满足于就题论题，那将停留在较低的层次。

于是我将评讲作业和拓展思维归为一类。评讲一道题，归纳一类题，在评讲时要注重变式训练，从本题出发向外辐射，把与该题有关的知识融入其中，形成网络，使学生能充分理解这类问题的本质联系，形成解题能力。

例6.直角梯形ABCD中，AD∥BC，∠C=∠D=90°，其中 BE平分∠ABC交 CD于点 E，BE⊥AE，试说明：AD+BC=AB。

变换1：在梯形ABCD中，AD∥BC，其中BE平分∠ABC交CD于点E，BE⊥AE，试说明：AD+BC=AB。

变换2：在梯形ABCD中，AD∥BC，E为CD的中点，BE⊥AE，试说明：AD+BC=AB。

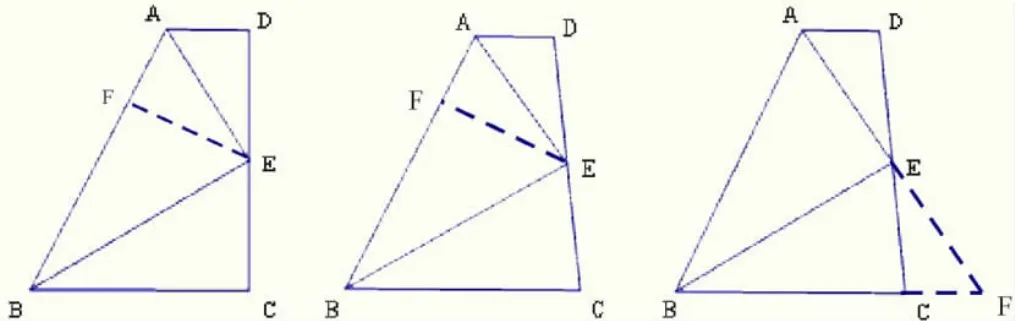
分析：例6的解题思路沿用例3，线段数量关系可利用全等转移到同一直线上进行，或转移到长边上进行分割，或转移到短边上进行补全。在例6中，“BE平分∠ABC交AD于点E”，要充分地利用条件，一定要抓住条件所在的图形，从而在AB上截取BF=BC，得△BCE≌△BFE，再证，便可得解。变换1中，将原题中的直角梯形变为一般梯形，使解题经历一个由“特殊到一般”的变通思维过程。变换2中，变换条件“E为AD的中点”，要利用中点制造全等的话，只可将AE延长交BC延长线于点F，使△ADE≌△FCE，将BC补全。

整道题中思维的路径是一致的，思维的起点都是全等，而由于条件的不同，使得思维的路径也有所不同，这就是变式的训练，由此提高学生的分析解题能力。

在平时的作业布置及评讲中，我们不仅要关注整体，而且要注重个体的发展需求。教师只有正确地理解作业的价值，更新教育观念，落实新课程理念，以学生的发展为本，加强作业的改革，最终才能让学生的知识在作业中升华，技能在作业中掌握，能力在作业中形成，思维在作业中发展。