自由表面波和水体压缩性对深水桥墩地震动水压力的影响

黄 信，李忠献

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

自由表面波和水体压缩性对深水桥墩地震动水压力的影响

黄 信1,2，李忠献1,2

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

地震时深水桥墩会受到动水压力作用，深入分析深水桥墩地震动水压力具有重要意义.基于辐射波浪理论建立深水桥墩地震动水压力计算公式，分析自由表面波和水体压缩性对动水压力的影响.研究表明：自由表面波仅在荷载激励频率较低时影响水面附近的动水压力；水体压缩性仅在荷载激励频率较高时影响动水压力.因此，在长大桥梁地震灾变过程模拟中可忽略自由表面波和水体压缩性对深水桥墩地震动水压力的影响.

深水桥墩；地震动水压力；自由表面波；水体压缩性；辐射波浪理论

深水桥梁的地震响应分析需要考虑水体和桥墩的动力相互作用，流体与结构相互作用分析方法主要有解析法[1-2]、数值法[3-5]和混合法[6-8].解析法是先求得桥墩所受的地震动水压力解析解，然后将动水压力代入桥墩结构的振动方程，从而对桥墩结构进行动水压力作用下的地震响应分析，其中桥墩结构的振动方程采用剪切梁或弯曲梁的振动方程；解析法仅能对简单的桥墩结构进行分析，同时由于桥墩按悬臂梁进行处理，所以不能考虑桥梁上部结构对桥墩的影响.数值法主要是利用有限元法或边界元法进行求解.有限元法将水体和结构均采用有限元进行离散，根据单元的目标函数不同可以分为 3类，即欧拉法、拉格朗日法和任意拉格朗日-欧拉法，然而由于水体和结构计算自由度较大，对计算机性能要求高、计算效率低.边界元法可将三维问题转化为二维问题，并且只需求解边界节点上的积分方程，计算成本相对较低.混合法是先求得地震动水压力的解析解，再采用有限元法建立桥墩结构分析模型，进而对桥墩进行动水压力作用下的地震响应分析.由于利用有限元建立桥墩模型，可以方便地考虑桥梁上部结构对桥墩的影响，同时仅对桥墩建立数值模型，相对数值法而言混合法计算效率高.

由于混合法的上述优点，现有深水桥墩地震响应分析主要采用混合法，而混合法的重点是桥墩地震动水压力的求解.Goyal等[6]研究具有 2个对称轴的任意截面形状柱体的动水压力，并考虑了土-结构相互作用.Mccormick[7]推导了柱体结构的动水压力公式，讨论了波数对惯性力系数及阻尼系数的影响.赖伟等[8]基于辐射波浪理论提出了一种计算动水压力的半解析半数值解，采用梁单元有限元方法求解耦联运动方程.上述研究均基于辐射波浪理论建立动水压力计算公式，动水压力会受自由表面波和水体压缩性的影响，自由表面波和水体压缩性的影响在坝体等结构物的地震动水压力分析中已经有相关研究，而目前有关自由表面波和水体压缩性对桥墩地震动水压力的影响鲜见系统性的研究.

笔者基于辐射波浪理论建立深水桥墩地震动水压力的计算公式，分析了自由表面波和水体压缩性对桥墩动水压力的影响.

1 基于辐射波浪理论的深水桥墩地震动水压力

首先考虑地面做简谐运动，荷载激励频率为ω.假定水体无旋并根据线性辐射波浪理论，此时在柱坐标系下水体的速度势Φ可表示为复数形式Φ(r, θ ,z,t) = φ(r, θ ,z) eiωt，其中φ(r,θ,z)为速度势空间因子.图1所示为深水桥墩分析示意.

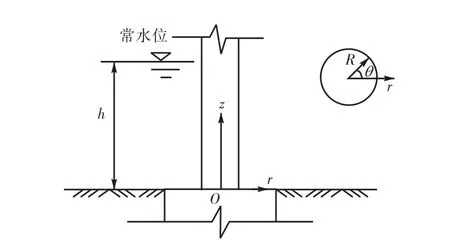
图1 深水桥墩分析示意Fig.1 Schematic diagram of bridge pier in deep water

水体控制方程为

整个水体的底面和表面以及水体与桥墩交界面处还要满足相应的边界条件，其中水与桥墩交界面的边界条件为

式中：R为圆柱体桥墩半径；h为水深；k＝ω/c，其中c为水中声速；u为桥墩的位移，本文仅考虑桥墩做刚体运动，桥墩弹性振动也可按此类似分析，地面简谐运动下的桥墩位移为 u = ug(t) = ugeiωt，其中 ug为位移幅值；柱坐标系中 z轴沿桥墩轴线向上，坐标原点位于墩底.

将式(7)代入相应的控制方程式(1)，并结合边界条件式(2)～式(5)，可求得流场中的速度势.将求得的速度势代入 Bernoulli方程，可得到地面简谐运动下的桥墩动水压力，即

由式(8)可知考虑水体压缩性和自由表面波影响时，动水压力与结构运动频率有关.当忽略水体压缩性时c→∞，从而得到 k＝0.当忽略自由表面波影响时0λ=，并且自由表面边界条件

由于任何振动可以用傅里叶变换分解成简谐振动，对于实际地震动可将加速度时程通过傅里叶变换得到频域中的谐幅函数，从而可以得到实际地震动下的桥墩动水压力.

2 自由表面波对动水压力的影响

水体表面处任意区域激发局部扰动，产生以重力波形式向周围传播的波称为自由表面波.为衡量自由表面波对动水压力的影响，忽略水体压缩性对桥墩动水压力进行分析.

桥墩动水压力采用无量纲参数，动水压力系数为式中：Cp为动水压力系数；abs(Cp)表示对动水压力系数Cp取模.

2.1 动水压力系数沿桥墩高度的分布

为分析自由表面波对动水压力的影响，沿桥墩高度计算动水压力系数，其中考虑自由表面波时荷载激励频率ω分别取 1,rad/s、2,rad/s和 12,rad/s；桥墩水深h＝40,m，截面半径R分别取2,m和4,m.图2所示为动水压力系数沿桥墩高度的分布.

从图 2(a)可以看出，桥墩半径 R＝2,m 时，当荷载激励频率(ω＝12,rad/s)较高时，动水压力系数沿桥墩高度分布和忽略自由表面波影响下的动水压力系数分布一致；对于荷载频率(ω＝1,rad/s和ω＝2,rad/s)较低时，桥墩墩底到桥墩高度 35,m 处的动水压力系数和忽略自由表面波影响下的动水压力系数差别不大，仅在水面附近有所增加，如忽略自由表面波时水面处(z＝40,m)的动水压力系数为 0，ω＝1,rad/s时水面处的动水压力系数为 1.32，ω＝2,rad/s时水面处的动水压力系数为 1.76.为更加详细地分析自由表面波的影响，沿桥墩高度对动水压力进行积分，可得到桥墩总的动水压力，当忽略自由表面波效应时总动水压力系数为 37.66，而ω＝1,rad/s和ω＝2,rad/s时总动水压力系数分别为 40.73和 37.96，可知考虑自由表面波效应时动水压力的增幅均小于8%，所以相对桥墩所受的总动水压力而言自由表面波影响可以忽略.对于图2(b)中桥墩半径R＝4,m时也可以得出类似规律.

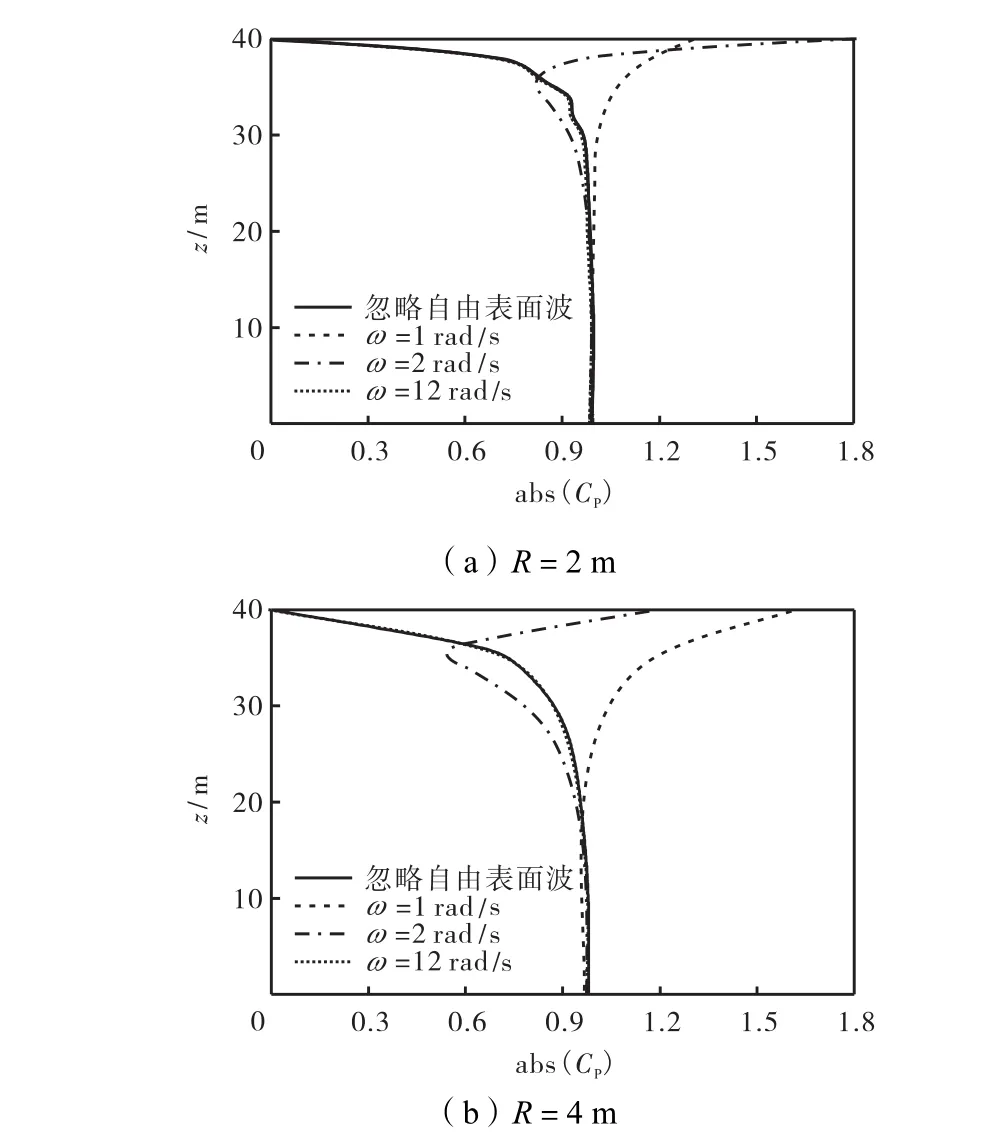
图2 自由表面波影响下动水压力系数沿桥墩高度的分布Fig.2 Hydrodynamic pressure coefficient distribution with Fig.2 pier height considering free surface wave

2.2 动水压力系数随荷载激励频率的分布

进一步分析动水压力系数随荷载激励频率的变化，分别计算桥墩墩底、桥墩高度20,m处和水面处的桥墩动水压力系数.图 3所示为动水压力系数随荷载激励频率的分布.

从图 3(a)可以看出，桥墩半径 R＝2,m 时，水面处的动水压力系数在荷载激励频率较低时会随荷载激励频率的变化而发生变化；而对于桥墩墩底和桥墩高度20,m处的动水压力系数随荷载激励频率的变化不明显.进一步说明了自由表面波仅在荷载激励频率较低时会对水面附近的动水压力产生影响.对于图3(b)中桥墩半径R＝4,m时也可以得出类似规律.

综上所述，荷载激励频率较高时自由表面波对桥墩动水压力的影响可以忽略；荷载激励频率较低时自由表面波仅会对水面附近的桥墩动水压力产生影响，相对桥墩总的动水压力而言这种影响也可以忽略.所以对于深水桥墩地震动水压力分析可以忽略自由表面波的影响.

图3 动水压力系数随荷载激励频率的分布Fig.3 Hydrodynamic pressure coefficient distribution with Fig.3 load excitation frequency considering free surface Fig.3 wave

3 水体压缩性对动水压力的影响

水体不可压缩是指水体密度在运动过程中保持为常数即不随时间和空间变化，而实际水体是可压缩的，为正确分析地震作用下深水桥墩的动水压力，有必要研究水体压缩性对桥墩动水压力的影响.

为衡量水体压缩性对动水压力的影响，忽略自由表面波对桥墩动水压力进行分析.荷载激励频率采用无量纲参数η表示，即

3.1 动水压力系数沿桥墩高度的分布

沿桥墩高度计算动水压力系数，其中η＝0表示忽略水体压缩性，考虑水体压缩性时分别取η＝0.03、η＝4和η＝7；桥墩水深 h＝40,m，截面半径 R分别取2,m和4,m.图4所示为动水压力系数沿桥墩高度的分布.

从图 4(a)可以看出，桥墩半径 R＝2,m 时，荷载激励频率(η＝0.03)较小时，动水压力系数沿桥墩高度分布和忽略水体压缩性(η＝0)时的动水压力分布一致；当荷载激励频率较大时，动水压力系数相对忽略水体压缩性下的动水压力系数有所变化，如忽略水体压缩性时墩底处的动水压力系数为 0.99，而η＝4时墩底处的动水压力系数为 1.07，η＝7时墩底处的动水压力系数为 1.12.同样对于图 4(b)中桥墩半径R＝4,m也可以得出类似结论.

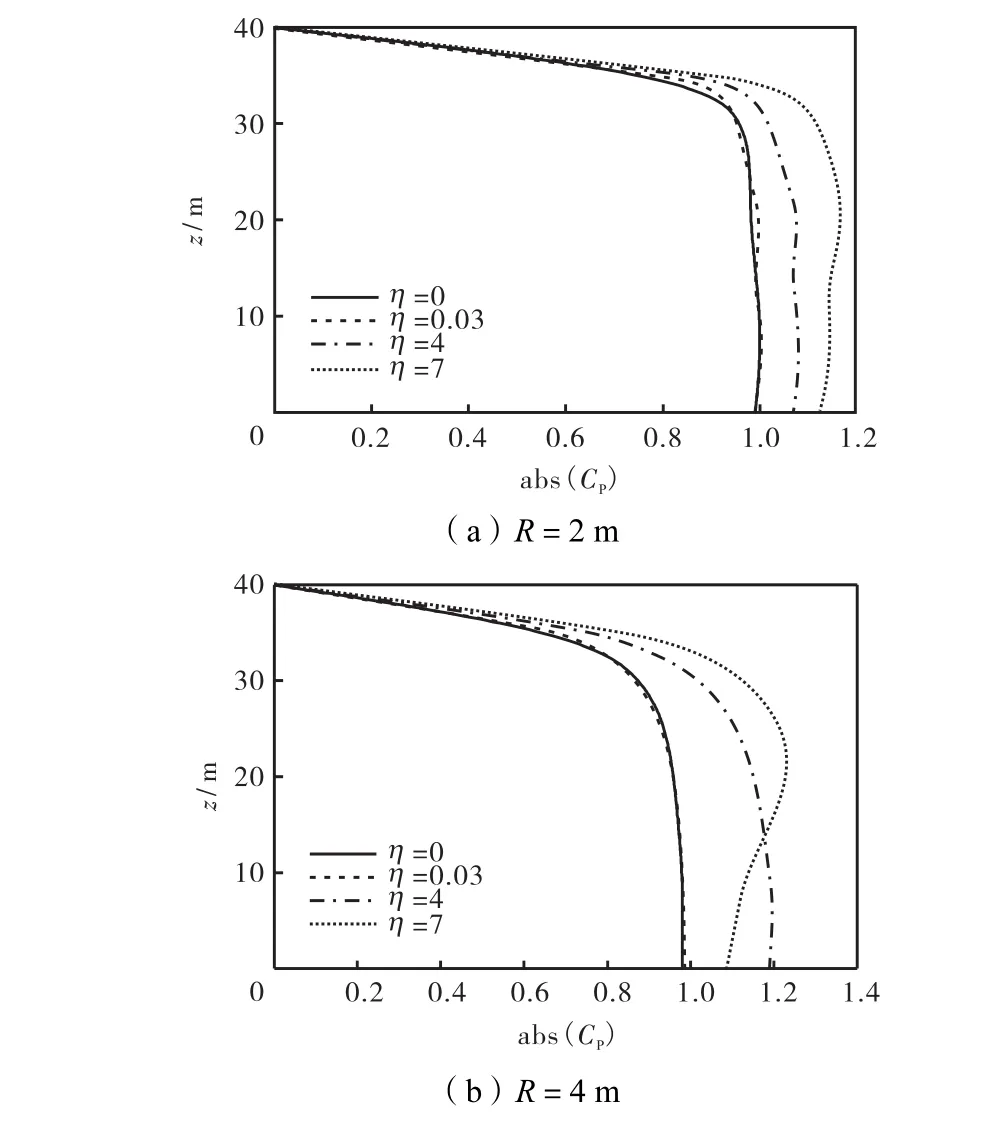
图4 动水压力系数沿桥墩高度的分布Fig.4 Hydrodynamic pressure coefficient distribution with Fig.4 pier height considering water compressibility

3.2 动水压力系数随荷载激励频率的分布

分析动水压力系数随荷载激励频率的变化，分别计算桥墩墩底处、桥墩高度 10,m 处、桥墩高度 20,m处和桥墩高度30,m处的动水压力系数.图5所示为动水压力系数随荷载激励频率的分布，其中横坐标采用对数坐标.

从图 5(a)可以看出，桥墩半径 R＝2,m 时，动水压力系数先随η的增加而增大，达到峰值后随η增加而减小；并且当η小于 2.5时动水压力系数变化较小，即水体压缩性对动水压力的影响不明显，利用式(14)可知η＝2.5时ω=89.4 rad/s，而一般地震作用的主要频率小于使水体压缩性产生明显影响的荷载激励频率，所以水体压缩性的影响可以忽略.对于图5(b)中桥墩半径R＝4,m也可以得到类似结论.

综上所述，荷载激励频率较低时水体压缩性对桥墩动水压力的影响可以忽略；当荷载激励频率较大时水体压缩性会对动水压力产生影响，而地震作用的主要频率小于使水体压缩性产生明显影响的荷载激励频率.所以深水桥墩地震动水压力分析中可以忽略水体压缩性的影响.

图5 动水压力系数随荷载激励频率的分布Fig.5 Hydrodynamic pressure coefficient distribution with Fig.5 load excitation frequency considering water Fig.5 compressibility

上述分析可知，深水桥墩地震动水压力分析可以忽略自由表面波和水体压缩性的影响.忽略自由表面波影响时自由表面边界条件满足式(11)，忽略水体压缩性时 k＝0，所以动水压力表达式(8)中不再包含荷载频率，即动水压力不随荷载激励频率变化，此时动水压力对桥墩地震响应的影响如同一附加质量.

4 结 论

(1) 自由表面波在荷载激励频率较高时对桥墩动水压力的影响可以忽略；自由表面波在荷载激励频率较低时仅会对水面附近的动水压力产生影响，相对桥墩所受的总动水压力而言这种影响也可以忽略.所以对于深水桥墩地震动水压力分析可以忽略自由表面波的影响.

(2) 水体压缩性在荷载激励频率较低时对桥墩动水压力的影响可以忽略；水体压缩性在荷载激励频率较大时会对动水压力产生影响，而地震作用的主要频率小于使水体压缩性产生明显影响的荷载激励频率.所以深水桥墩动水压力分析中可以忽略水体压缩性的影响.

(3) 当忽略自由表面波和水体压缩性影响时，动水压力不随荷载激励频率变化，此时可以利用附加质量概念对深水桥墩进行地震响应分析.

［1］居荣初，曾心传. 弹性结构与液体的耦联振动理论[M]. 北京：地震出版社，1983.Ju Rongchu，Zeng Xinchuan.Coupling Vibration Theory of Elastic Structure and Liquid[M]. Beijing：：Earthquake Press，1983(in Chinese).

［2］Zhou D，Liu W Q. Bending-torsion vibration of a partially submerged cylinder with an arbitrary crosssection[J].Applied Mathematical Modelling，2007，31(10)：2249-2265.

［3］Chen B F. The significance of earthquake-induced dynamic forces in coastal structures design[J].Ocean Engineering，1995，22(4)：301-315.

［4］Bathe K J，Zhang H，Ji S H. Finite element analysis of fluid flows fully coupled with structural interactions[J].Computers and Structures，1999，72(1)：1-16.

［5］Sun K，Nogami T. Earthquake induced hydrodynamic pressure axisymmetric offshore structures[J].Earthquake Engineering and Structural Dynamics，1991，20(5)：429-440.

［6］Goyal A，Chopra A K. Earthquake analysis of intakeoutlet towers including tower-water-foundation-soil interaction[J].Earthquake Engineering and Structural Dynamics，1989，18(3)：325-344.

［7］Mccormick M E. Hydrodynamic coefficients of a monolithic circular offshore structure[J].Earthquake Engineering and Structural Dynamics，1989，18(2)：199-216.

［8］赖 伟，王君杰，胡世德. 地震下桥墩动水压力分析[J]. 同济大学学报，2004，32(1)：1-5.

Lai Wei，Wang Junjie，Hu Shide. Earthquake induced hydrodynamic pressure on bridge pier[J].Journal of Tongji University，2004，32(1)：1-5(in Chinese).

Influence of Free Surface Wave and Water Compressibility on Earthquake Induced Hydrodynamic Pressure of Bridge Pier in Deep Water

HUANG Xin1,2，LI Zhong-xian1,2
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education，Tianjin University，Tianjin 300072，China)

Hydrodynamic pressure is applied to bridge pier in deep water under earthquake excitation. It is of great significance to analyze earthquake induced hydrodynamic pressure of bridge pier in deep water. Earthquake-induced hydrodynamic pressure formulary was established using radiation wave theory. The influence of free surface wave and water compressibility on hydrodynamic pressure of bridge pier was studied. The results indicate that free surface wave will only influence hydrodynamic pressure in the vicinity of water surface under low-frequency load excitation. Water compressibility only has an effect on hydrodynamic pressure under high-frequency load excitation. In conclusion，the influence of free surface wave and water compressibility on earthquake induced hydrodynamic pressure can be ignored in earthquake hazard simulation of long and huge bridge.

bridge pier in deep water；earthquake induced hydrodynamic pressure；free surface wave；water compressibility；radiation wave theory

U442.5

A

0493-2137(2011)04-0319-05

2010-07-22；

2010-09-02.

国家自然科学基金重大研究计划重点支持项目(90715032)；国家自然科学基金重大研究计划培育项目(91015005)；国家自基金项目：然科学基金重大国际合作项目(51021140003).

黄 信（1983— ），男，博士研究生，xhuang@tju.edu.cn.

李忠献，zxli@tju.edu.cn.