稀疏数据源频繁模式挖掘并行算法

郑晓艳，孙济洲

(1. 天津大学计算机科学与技术学院，天津 300072；2. 天津职业技术师范大学信息技术工程学院，天津 300222)

频繁模式挖掘在数据挖掘中起着非常重要的作用，目前已经提出的频繁模式挖掘算法大致可归结为2类．第 1类是产生候选集的算法，这类算法主要应用 Apriori性质[1]，递归地从 k频繁模式中产生 k+1候选模式，通过扫描数据库确定一个候选模式是否是频繁的．第 2类是基于 FP-tree[2]的方法，该方法建立一棵前缀树，称为 FP-tree，只对数据库扫描一遍，将数据库所包含的模式信息保存在这棵树上，从 FP-tree上挖掘频繁模式．在以上方法的基础上发展了相当多的并行算法，影响较大的有 CD(count distribution)算法、DD(data distribution)算法[3]，PDM (parallel data mining)算法[4]．CD算法在各处理器上水平划分数据库，采用冗余计算避免处理器之间的通信，所以该算法的通信量小，但是不能充分利用整个系统的内存．DD算法在处理器之间划分频繁项集，解决了计算规模可以随节点个数增加而增加的问题，但是处理器之间的广播带来了很大的通信负载，在节点增加时也增加了通信的开销．CD算法和DD算法都存在对每个候选集需要扫描整个数据库的问题，以及每次扫描结束时各个处理器需要同步的问题．PDM 算法和CD算法类似，用Hash表维护局部候选k项集．为了构成全局候选项集，采用一种称为 clue-and-poll的技术，只选取少量可能满足支持度要求的表项在处理器之间交换，并且实现了Hash表的并行生成，算法在候选集增大的时候有较好的可扩展性．

MLFPT(multiple local frequent pattern tree)算法[5]是在共享存储结构上提出的基于 FP-tree的频繁项集挖掘算法．均匀划分数据库，每个处理器生成一个局部频繁模式树，并在所有处理器之间共享．只对数据库扫描 2次，而且不会产生大量频繁项集，对长规则的适应性很强．但是当处理稀疏数据时，由于FP-tree上的可共享节点减少，造成树结构过大，效率甚至低于Apriori类算法．

实际上，很多应用数据库呈现稀疏状态，如超市的销售数据库．有少部分文献论述了当数据源为匀质或非匀质时算法的运行效率问题以及解决方法．但专门针对某种特殊数据源进行的研究还不多见．陈惠萍等[6]针对稀疏数据源提出了 FP-tree和支持度数组相结合的方法挖掘最大频繁项集，用二维数组保存所有可能的频繁2项集的支持度，用于查找某个项目的条件模式库中的所有频繁项．文献[7]中也用到了类似的二维矩阵．该方法减少了遍历 FP-tree的次数，但是也引入了一定的时间和空间开销．而且仍然采用 FP-tree存储数据库信息，如果对其并行化，建立FP-tree仍然是算法的瓶颈．

另外，由于消息传递模型和共享存储模型在计算性能上的明显差异，大部分算法都是在消息传递计算模型上提出的．实际上，共享存储计算模型在程序设计时由于不需考虑消息传递的时间、对象和内容，编程方面具有非常大的优势，但在传统的共享存储模型上，这些程序设计方面的优势也正是计算性能差的主要原因．为了提高共享存储计算环境的性能，Huang等[8]提出了一种面向视图的并行编程(view oriented parallel programming，VOPP)思想，用视图作为一致性维护的基本单元．程序员可以根据算法特点把数据对象划分成多个视图．VODCA (view-oriented，distributed，cluster-based approach)[9]是基于 VOPP 实现的面向视图的分布式集群计算方法，实现了一致性维护中的时间选择、处理器选择和数据选择，借鉴了Trademarks的内存维护策略并进行改进，解决了Trademarks中 diffs积累问题．使得其计算性能较传统的共享存储计算环境有了很大的提高[10]．

本文针对稀疏数据源，设计了一种链表结构，提出了稀疏数据源频繁项集挖掘并行算法(parallel mining frequent itemsets from sparse data source，PMFSD)，并在VODCA上实现．

1 FI-list设计和构造

为了提高频繁项集的计算速度，FI-list的设计和构造主要从3个方面加以考虑：①减少数据库扫描次数以降低 I/O数量；②及时有效地对数据进行剪枝以减少候选集的数量；③避免保存大量候选项集以降低内存占用量．

1.1 FI-list的设计

链表结构体 FI-list的设计借鉴了稀疏矩阵的列压缩存储策略．稀疏矩阵的基本列压缩存储格式是使用 3个数组 AA、JA和 IA，数组 AA存储按 1～n列排列的非零矩阵元素，整型数组JA表示AA中对应元素所在的行号，整型数组 IA中的元素是每一列的开始在 JA中的索引号．把源数据库看作一个稀疏矩阵，每个事务表示一个行向量，每个项目代表一个列向量．如果频繁模式挖掘中使用的输入数据是二元的，即只要求明确项目是否是非零的，数据源就可以被看作一个二元稀疏矩阵，如图1所示．

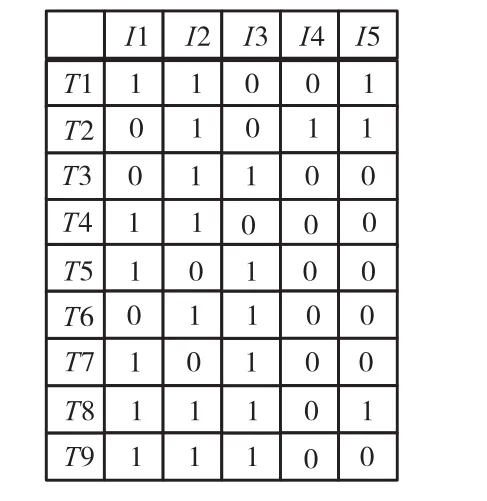
图1 示例数据源Fig.1 Instance of data source

该矩阵采用标准列压缩格式可以存储为

因为矩阵是二元的，非零数据即是 1，无须专门记录，所以数组 AA可以省略．本文在此基础上对以上表示方法加以改造，只保留数组JA．在其中增加每个列的开始标记，这里用数字0来表示．

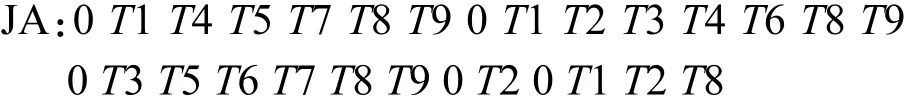
算法实现中可以对以上存储结果进一步压缩，根据设定的最小支持数，从中去除支持数小于最小支持数的项集所对应的列信息，例如，最小支持数为2时，上述矩阵最终变换为

经过对数据库的二元映射和存储变换之后，对频繁项集的计数扫描就可以在一维链表上进行了．

如图 2所示，链表结构体由 2部分构成：项目头表(HB)和事务链表(TL)．其中HB用于存放产生的频繁项集和相应的支持度、地址信息，每一个表项有3个域，内容(Contents)域保存项集内容，支持度(Sup)域保存各项集的支持度，地址(Add)域存放与该项集相关的事务链表头．TL是一个线性链表，存放与项集相关的事务号(TID)序列．事务号序列T(ISi)＝Ti,k1，Ti,k2, … ,Ti,ksi(i = 1,2,… ,n )，其中 k1＜ k2＜ …＜ksi．

图2 频集链表结构体Fig.2 Unit of frequent itemsets list

数据集越稀疏，与每个项目相关的事务数目越少，相关的交易链长度越小．通常在频繁 2-项集之后，随着频繁项集长度增加，相关的事务数目急剧减少，整个链表尺寸很小，容易装入内存．但在非稀疏数据集情况下，由于链结构的开销，整个链表实际尺寸会大于相应的二元数据库，需要更多的存储空间．

FI-list结构也可以在其他共享内存编程环境和消息传递平台上使用，作为稀疏数据源频繁项集挖掘的数据结构．在消息传递平台上，整个 k-项集相关信息和链表可以在处理器之间进行复制，作为计算k+1项集的依据．另外需要一个事务长度表 LB，记录每个事务的长度，用于产生候选集时的剪枝条件．

1.2 FI-list的构造

构造FI-list有如下4个步骤．

(1)对数据库按行扫描一次，统计各个事务的长度，生成LB．

(2)对数据库按列扫描一次，按设定的最小支持度，生成频繁 1-项集；每生成一个频繁 1-项集，按第1.1节中TM所示的顺序向事务细节表TL写入与该项目相关的事务号序列，同时向头表HB中写入该列对应的项目内容和支持度，并且使地址域指向TL．

(3)按照 Apriori性质，从(k-1)-项集生成 k-项集，同时根据 LB表进行剪枝．此过程由函数 Gen()递归实现．

(4)直到不能生成更高维频繁项集，FI-list构造结束．此时FI-list中保存了所有频繁项集及其支持度．

Gen函数所包含的算法如下：

2 VODCA环境下PMFSD算法实现

2.1 VODCA编程环境的特点

VODCA程序编译使用标准C或者C++编译器，程序中只须包含其提供的头文件，即可调用并行计算所需的相关系统常数和视图操作原语．程序员的主要工作是根据算法和数据结构的特征，把共享数据划分成视图，并且在程序中正确使用视图．对视图的划分和使用要考虑4个特点：①视图的内容可以根据算法和数据的特点任意划分；②视图一旦确定，在整个程序中不能改变；③每次只能对一个视图进行排他访问，但是允许对一个或多个视图嵌套使用只读访问；④无论算法中对共享数据的访问是否存在争用，任何对共享数据的操作(包括只读访问和读写访问)都必须调用视图访问原语(只读访问原语或者排他访问原语)．

2.2 问题中的视图定义

由于共享内存结构上编程的方便性，算法实现不必考虑数据的分布．根据 VOPP的特点，划分视图成为了算法实现的焦点问题．算法中涉及到的共享数据包括：数据源 DB、事务长度表 LB和 FI-list．其中对DB的共享访问是只读的，整个DB可以定义为一个视图．生成 LB时需要进行写访问，可以按任务划分定义视图，例如有 n个处理器，则对事务长度的统计就划分成n个任务，每个任务相关的LB部分定义为一个视图．FI-list要保存所有的频繁项集，每次产生一个新的频繁项集，都会发生对它的写操作，所以对FI-list相关视图的划分是程序设计的重点．

视图划分结果如图 3表示．对项目头表 HB，每个 k-项集(k＝1，2，…，m)的全体划分为一个视图，而对事务链表 TL，每个链划分为一个视图．这些视图都是在算法运行过程中动态产生的，每个视图可以通过编程获得唯一的编号．这样划分视图主要依据以下3个方面．

(1) 每个 k-项集的相关信息只在生成 k-项集时要求读写访问，在使用 k-项集生成(k+1)-项集时，k-项集的相关信息是只读共享的．所以只需考虑在生成k-项集时对数据对象访问的特点．

(2) 每个处理器每次向 HB写入一个 k-项集信息时，首先必须互斥地获得一个表项地址，所以对HB表尾的一次排他访问是不可避免的，将 k-项集的全体定义为一个视图，可以直接保证这个排他访问．另外由于向 HB中写入的信息相对较少，只有 3个数据，所以不会形成严重的计算瓶颈．

(3) 每个项集相关的事务数目相对较多，特别是在 k值较小时更是如此，为了提高算法的并行度，应该允许多个处理器同时生成各自的事务链．所以每个事务链定义为一个视图．

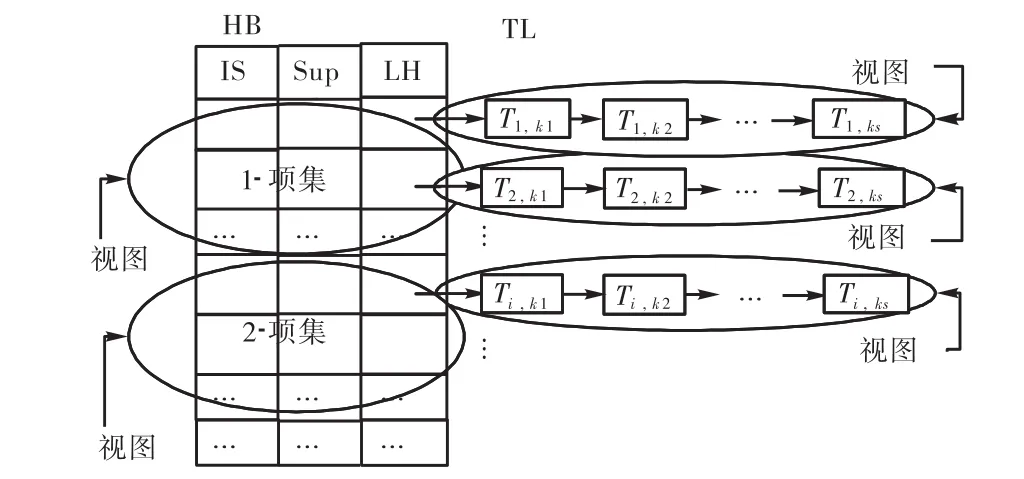
图3 视图划分结果Fig.3 Division of views

2.3 任务分配方案

算法的执行分成 2个阶段：第 1阶段，2次扫描数据库，第1次生成事务长度表LB，第2次生成频繁1-项集和对应的事务细节表；第 2阶段，生成频繁 k-项集．第1阶段采用静态任务分配策略，设有n个处理器，则把任务平均划分成 n个，各处理器各自生成一部分频繁 1-项集．在算法的第 2阶段，设系统中有n个处理器，m 个(k-1)-项集．则每次生成 k-项集的任务划分成 m-1个，任务 i(i＝1，2，…，m-1)对应第 i个(k-1)-项集与第 j个(k-1)-项集的连接，其中j＝i+1，i+2，…，m．所有处理器在生成 k-项集开始之前同步，并将全部(k-1)-项集放到本地的局部数据对象上，每次处理器 p取到一个任务并完成之后，将本次得到的k-项集加入HB．

显然，随着 i的增加，第 i个(k-1)-项集的连接对象有 m-i个，任务的计算量逐渐减少．另外由于一个任务连接生成的项集不一定是频繁的，即一个任务中是否包含支持度计数和写回全局 FI-list是不确定的，所以任务的大小是未知的．在任务数量和每个任务的大小都是动态确定的情况下，为了保持各个进程之间的负载平衡，这个阶段采用动态任务分配．采用任务池模型，定义一个读写视图 V，用于控制任务分配．V的值对应当前任务编号，取值范围[1，m-1]．处理器在取到一个任务之后，对V执行增1操作．

2.4 算法描述

算法的第 1阶段比较简单，这里不再详细描述，下面给出算法第2阶段的描述．

对于系统中的第i个节点，

输入：FI-list中的(k-1)-项集以及相关事务链表；最小支持度min_sup；

3 实验结果及分析

3.1 实验结果

实验所用的集群由16台运行Red Hat Linux9.0的个人计算机构成，通过100,Mb/s交换机连接．每台计算机带有 650,MHz的处理器和 128 M 内存，硬盘16,G，虚拟页面大小为4,kB．实验所用的数据库是某超市的销售数据库，共 250,850条事务，所卖商品划分为107个类别，有用数据量约为20%，实验用来发现这些商品类别在销售中的关系．

实验分别做了3个方面的研究：①为了考察PMFSD在处理节点增加情况下的可扩展性能，在数据量和最小支持度不变、节点个数变化情况下计算算法的加速比；②为了观察PMFSD算法对数据量的可扩展能力，在节点数量确定为8、支持度确定为1%，事务数量变化情况下计算算法的运行时间；③为了观察PMFSD算法对数据源稀疏程度的适应能力，采用随机生成的二元矩阵(事务200,000条，项目50个)，在支持度确定为1%，数据稀疏程度不同情况下比较PMFSD算法的运行时间．为了对比算法的性能，选择了MLFPT算法[5]，MLFPT也是在共享存储结构下实现的，在系统结构上具有可比性．实验结果见图4～图6．

图4 PMFSD的加速比Fig.4 Speedup of PMFSD on VODCA

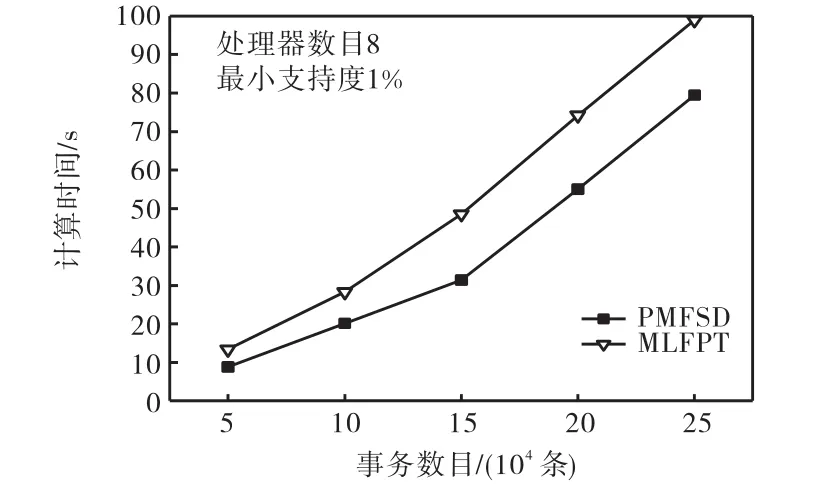
图5 事务量变化运行时间Fig.5 Running time on different number of transactions

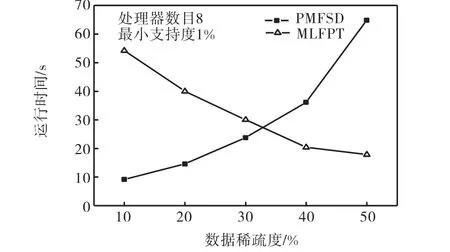
图6 稀疏度变化运行时间Fig.6 Running time on different sparse data sources

3.2 结果分析

图 4的实验结果显示加速比在处理器数目小于8时基本保持线性增长，但是在 16个处理器时增加幅度减小．这是因为处理器增多时系统中存在的同步消息增多，对共享数据的竞争加剧，这个情况可能会随着问题规模的变化而有所变化．图5显示当处理的事务数量增加时，2种算法的运行时间比较．PMFSD运算效率呈先增加后降低的趋势，在150,000条数据左右，效率最高，之后开始下降．开始效率增加是因为随着计算量的增大，计算/通信比增加．而数据量增大的同时，每个节点上的内存需求增大，特别是在支持度较小时，频繁 1-项集和频繁 2-项集的数量都很大，可能由于缺页中断，而使得计算速度下降．同样，数据稀疏程度的变化也会产生类似情况．这种情况也能从图 6所示的实验结果中得到验证，数据集越稀疏，与每个项目相关的事务数目越少，相关的交易链长度越小．通常在频繁2-项集之后，随着频繁项集长度的增加，相关的事务数目急剧减少，整个链表的尺寸很小，容易装入内存，所以计算速度很快．当非零数据增多时，由于链结构的开销，整个链表尺寸实际上会大于相应的二元数据库，需要驻留本地内存的数据增多，处理换页的开销达到一定比例，就会致使计算速度下降．采用MLFPT算法时，数据源越稀疏，FP-tree上的共享前缀越少，产生的 FP-tree也就越大，在生成 FP-tree和计算条件模式库时会明显增加扫描时间，从图 6可以看出，2种算法随数据源稀疏度变化的运算时间对比非常显著．

算法的执行时间由4个部分组成：系统启动时间tstart，扫描数据库所需时间 tscan，连接和依照单调性剪枝时间 tconn，计算支持数和写入链表信息所需时间tlist．其中 tstart由系统确定．扫描数据库时间 tscan涉及到实际计算时间和数据装入本地所需的通信时间，可以描述为数据规模的线性函数，不对性能评价产生影响．频繁 k-项集的数目与最小支持度和项目数有关，当数据源为稀疏数据源时，频繁2-项集之后的频繁项集数目会急剧减少，tconn主要发生在频繁 3-项集产生之前，当频繁项集数目增加时，HB的尺寸增大，连接和剪枝操作会导致更多的换页，换页概率正比于频繁项集数目．项集的支持数计数和写入事务细节的时间 tlist与事务数目和数据稀疏度有关，当与一个频繁项集相关的事务数目较大时，tlist中的缺页处理时间比例上升．以上4部分中影响算法效率的主要因素是 tconn和 tlist．若处理器数目确定，页面尺寸为 M，处理缺页中断所需时间用 tf表示，事务数目为 N，最小支持度阈值为S，这2部分时间描述为

式中：hi是频繁 i-项集的数目；ti为产生一个 i-项集所需的连接和依照单调性剪枝时间；tij是对第 j个 i-项集进行统计支持度和写入链表时间；B1、B2是与编程有关的数据长度．

在只增加挖掘数据源中事务数量 N的情况下，式(1)的值是固定不变的，图 5中性能下降的因素是式(2)．而图 6性能下降的因素则包括式(1)和式(2)2部分，在支持度不变的情况下，有用数据量的增加，使得产生的频繁项集数目显著增加，从而大幅地提高了运算时间．

4 结 语

本文在一个新的分布式共享内存编程环境VODCA上，针对稀疏数据源上的频繁项集搜索问题，提出和实现了一个新的算法PMFSD，并通过实验验证了算法的有效性．PMFSD算法同样可以在消息传递平台上实现，实现的关键是FI-list的构建．

［1］ Agrawal R，Srikant R. Fast algorithms for mining association rules in large databases[C]//Proceedings of20th International Conference on Very Large Data Bases(VLDB'94)．Santiago de Chile，Chile：Morgan Kaufmann，1994：489-499.

［2］ Han Jiawei，Pei Jian，Yin Yiwen. Mining frequent patterns without candidate generation[C]//Proceedings of the ACM SIGMOD Conference on Management ofData(SIGMOD'00)．New York：ACM Press，2000：1-12．

［3］ Agrawal R，Shafer J C．Parallel mining of association rules[J].IEEE Trans on Knowledge and Data Engineering，1996，8(6)：962-969.

［4］ Park J S，Chen M，Yu P S. Efficient parallel data mining for association rules[C]//ACM Intl Conf of Information and Knowledge Management．New York：ACM Press，1995：31-36．

［5］ Zaïane O R，El-Hajj M，Lu P. Fast parallel association rule mining without candidacy generation[C]//Proceedings of the2001IEEE International Conference on Data Mining. San Jose，USA：IEEE Computer Society，2001：665-668.

［6］ 陈惠萍，王建东，叶飞跃，等. 基于 FP-tree和支持度数组的最大频繁项集挖掘算法[J]. 系统工程与电子技术，2005，27(9)：1631-1635.

Chen Huiping，Wang Jiandong，Ye Feiyue，et al. Efficient mining maximal frequent itemsets by using FP-tree and support array[J].Systems Engineering and Electronics，2005，27(9)：1631-1635(in Chinese).

［7］ 徐维祥，苏晓军. 基于频繁模式树的一种关联规则挖掘算法及其在铁路隧道安全管理中的应用[J]. 中国安全科学学报，2007，17(3)：25-32.

Xu Weixiang，Su Xiaojun. A high-performance association rule mining algorithm based on FP-tree and its application in railway tunnel safety management[J].China Safety Science Journal(CSSJ)，2007，17(3)：25-32(in Chinese)．

［8］ Huang Z，Purvis M，Werstein P. View-Oriented Parallel Programming and View-Based Consistency[R]. Technical Report(OUCS-2004-09)，Dept of Computer Science，Univ of Otago，2004.

［9］ Huang Z，Chen W，Purvis M，et al. VODCA：Vieworiented，distributed，cluster-based approach to parallel computing[C]//Proc of the IEEE/ACM Symposium on Cluster Computing and Grid2006(CCGrid06)．Singapore：IEEE Computer Society，2006：15-28.

［10］ Huang Z，Purvis M，Werstein P. View oriented update protocol with integrated diff for view-based consistency[C]//Proc of the Fifth IEEE International Symposium on Cluster Computing and Grid2005(CCGrid′05)．Cardiff，UK：IEEE Computer Society，2005(2)：873-880．