供水管网的摩阻系数校核与漏损定位计算方法

牛志广，王宇飞，张 珽，张宏伟

(1. 天津大学环境科学与工程学院，天津 300072；2. 山西华宇集团，太原 030002)

随着城市供水管网设备的老化、技术和管理的相对滞后，供水管网的漏损问题日益突出，统计资料表明，我国城镇供水管网的漏损率在 1993年为 9.82%，但 2005年已经达到 18.02%[1]．管网漏损不仅浪费了宝贵的水资源，更加重了城市用水日益紧缺的形势，同时也损害了供水企业的经济利益，较为明显的漏损形式还会对周边环境乃至生产、生活产生负面影响.因此，当爆管等管网漏损现象发生时，要及时发现并进行较为准确的定位．目前国外很多学者在这方面已做过不少研究，Liggett教授及其研究小组先后提出了逆分析法[2]、瞬态分析与遗传算法[3]和阻尼法等漏损定位方法[4]．Kapelan等[5-6]运用水力模型和优化算法对管网参数进行校核并开展漏损定位研究，通过实例运算取得了满意的结果．以上这些研究均基于压力和流量的分析，在漏损诊断的速度和精度方面有显著提高．但是，为了实现供水管网的实时漏损定位，有必要进一步提高漏损管网模拟的精度，即在进行压力和流量分析的同时，对管网模型参数进行校核．为了避免实际管网的复杂性和不可验证性，本研究以实际管网为基础建立了实验管网，并尝试建立了2种优化模型：管网摩阻系数校核与漏损节点定位的分步优化模型和联合优化模型，均采用粒子群优化(particle swarm optimization，PSO)算法对模型进行求解．

1 研究对象与方法

1.1 研究对象

本研究使用的实验管网依据变态相似理论[7]，按照某开发区实际供水管网搭建．管网拓扑结构如图 1所示，实验管网包含2个供水点，分别由1#水泵和2#水泵提供；管网有53个节点，84根管段，管材全部为镀锌钢管，管径 DN15～DN50；漏损模拟点 6个，大用户节点6个，压力监测点9个．

图1 实验供水管网结构Fig.1 Structure of the experimental water supply network

1.2 管网模拟方法

在本研究中，主要使用 EPANET的水力模拟功能，模拟不同摩阻系数和漏损状态下管网各压力监测点的水压数据，通过对比模拟数据和实际测量数据之间的差异，校核管网模型参数并对漏损节点进行定位.

参照第1.1节中的实验管网，建立了EPANET下的对应管网模型，采用海曾-威廉水头损失公式作为沿程水头损失计算方法，管段初始设计摩阻系数设置为 120．

1.3 供水管网摩阻系数校核与漏损定位的分步优化模型

管网模型参数的校核是建立管网模型的一个重要步骤，影响管网模型准确性的参数有很多，其中节点流量、摩阻系数的确定人为因素干预最大．但随着管网基本数据的日趋完善，节点流量的估计趋于准确，摩阻系数的校核就成了管网模型参数校核中的重点．对于实验室条件下构建的模拟管网，实现了较为准确的节点流量控制，因而这里仅考虑摩阻系数作为管网模型参数校核的对象．通过摩阻系数校核，得到与设计管网更为接近的管网模型．由于该模型与实际模型的高度吻合，在此模型的基础上再建立管网的漏损定位模型，才能准确求解出漏损节点位置．这种先校核摩阻系数再进行漏损定位的模型，即是分步优化模型，以下将分述各步中具体优化模型的建立方法．

1.3.1 摩阻系数校核优化模型

摩阻系数的校核需要通过对管网的压力监测进行反分析，从而得到符合实际运行情况的摩阻系数．该问题可以归结为一个优化过程，即在管网不同运行状态下通过校核管网的摩阻系数，最大程度地满足模拟计算压力值与实验监测压力值的吻合．实际研究中采用管网压力实测值与计算值之差的二乘误差来评价水力模型与实际管网的相似程度，即采用的目标函数为

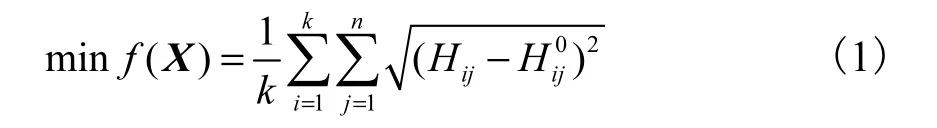
式中：f为待优化的目标函数；X为待优化的参数向量(此处为管道摩阻系数)；n为已知压力节点的个数；为第i个工况下第j个节点的实测压力，m；H 为ij第 i个工况下第 j个节点的计算机模拟压力，m；k为校核工况数．

式(1)表示了管网模型的计算结果和实际测量结果的差异．通过在 EPANET软件中反复进行不同摩阻系数 X时的管网运行状态模拟，得到模拟压力Hij．将不同摩阻系数状态时的模拟压力 Hij与实际监测压力 Hi0j进行对比，当两者差异达到最小时，即认为摩阻系数已经足够精确．

1.3.2 漏损节点定位优化模型

在进行模型参数校核后，管网的实际运行情况已经可以通过计算机模拟较为真实地呈现出来．同第1.3.1节中的原理，可建立如下供水管网漏损节点定位优化的目标函数，即

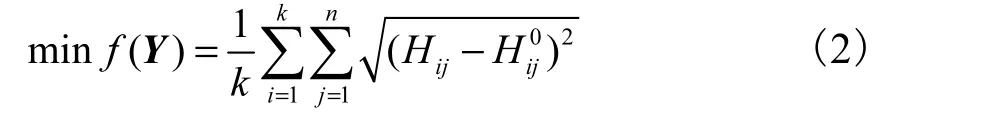
式中Y为待优化的参数向量(此处为假设漏损的管网节点编号)．其余参数含义同式(1)．

在该模型中，摩阻系数 X被换成了管网节点编号 Y，即通过假设某一管网节点漏水，将此时的模拟漏损管网运行状态与实际发生漏损的管网运行状态按照式(2)进行误差计算，并根据误差不断调整假设漏损点．当某次调整漏损点后的计算误差达到要求时，即认为假设的漏损节点就是实际的漏损节点．

1.4 供水管网摩阻系数校核与漏损节点定位的联合优化模型

管网在实际发生漏损时，不同的漏损程度与漏损位置势必对管网的摩阻系数带来一定变化，因此可以尝试将供水管网的模型参数校核和漏损的节点定位放在同一模型中进行联合优化，建立供水管网摩阻系数校核与漏损节点定位的联合优化模型为

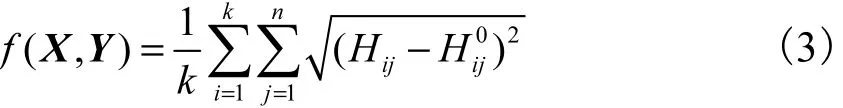
式中：X为管段的摩阻系数向量；Y为模拟漏损节点编号向量．

1.5 优化模型的求解

求解式(1)～式(3)中的优化模型需要选择一种合适的优化方法，经过对比爬山算法、遗传算法、蚁群算法和PSO算法等优化算法，可以发现PSO算法具有容易实现、精度高和收敛快的特点，因此本文选取PSO优化算法对第1.3节和第1.4节建立的2种优化模型进行求解．

PSO优化算法是Eberhart和Kennedy于1995年提出的一种模拟鸟群捕食行为的进化计算技术[8]，在PSO算法中，每个优化问题的解都被抽象成搜索空间中的“粒子”．PSO算法开始后，用于求解的粒子群首先被初始化为一群随机粒子，然后通过迭代找到最优解．在每一次迭代中，粒子通过跟踪 2个“极值”来更新自身状态：第一个极值是粒子本身所找到的最优解，称为个体极值 pbest；另一个极值是整个种群目前找到的最优解，称为全局极值gbest．找到这2个极值后，粒子再更新自己的速度和新的位置，其公式为

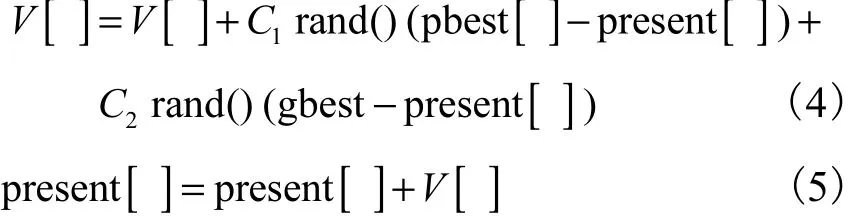
式中：V []为粒子的速度；present[]为当前粒子的位置；pbest []为个体极值；gbest为全局极值；rand()为介于(0，1)之间的随机数；C1、C2为学习因子，通常 C1＝C2＝2．

算法开始后，每个粒子都按照式(4)和式(5)更新速度和位置，然后根据被优化函数计算粒子的适应度，并通过适应度与个体极值和全局极值的对比结果按式(4)和式(5)再次更新速度和位置，如此反复，直到满足结束条件(误差足够小或达到最大循环次数)则退出循环．根据该原理，在Microsoft Visual C++6.0开发环境下编程实现 PSO优化算法，优化问题中的管网状态模拟过程由EPANET软件提供的Toolkit工具调用各种水力计算函数模拟完成．在程序中，管网的摩阻系数用粒子位置表示，优化模型中管网压力实测值与计算值之差的二乘误差用粒子的适应度表示.

1.6 实验方案

使用PSO优化算法求解第1.3节和第1.4节中的优化模型，需要足够多种不同工况下的压力监测点实际测量压力作为必要的校核与定位依据．为了保证采集数据的准确度和多样性，设计了以下实验方案.

实验中对于流量的测量采用了2种不同方法：①水泵出水口流量采用智能涡轮流量计测量，精度级别为 0.5级，半“U”型安装；②模拟漏损点和模拟大用户节点流量较大，不宜采用流量计量仪表，实验中采用体积法测量，即量筒(500 mL、1 000 mL)、水箱和秒表配合计量．压力的测量采用 0.4级精密压力表测量，装置中如水泵出口、管段上下游端及模拟测压点均采用此压力表测量．为保证压力监测结果的可读性与适用性，实验采取小流量、高压力的管网运行方式，两泵同时开启，保证回水量与供水量稳态平衡．

对于管网摩阻系数的校核而言，需要在几种差异较大的管网运行工况中获取多组运行数据才能保证校核结果对于各种运行状态都具有较好的适应性．因此，采用分别关闭、开启管网中大用户节点的方式形成不同的管网工况，为了保证所形成的不同工况间具有足够大差异性，选取了管网中相对距离较远的Ⅰ、Ⅲ、Ⅴ号大用户节点分别进行关闭、开启操作，并在管网稳定运行后读取压力监测点数据．通过分别关闭、开启3个大用户节点，形成了4种差异较大的管网工况，一共采集到 4组不同工况下的压力监测数据．这4组数据对于管网摩阻系数的校核而言是足够多的．

对于管网的漏损定位研究，可以利用实验管网中设置的水龙头模拟不同漏损状态．实验方案如下：首先，确保 6个大用户节点稳态运行；然后，分别逐点90°开启 6个模拟漏损点的水龙头，模拟管网的漏损状态，并同时测定龙头漏失水量、读取 9个压力监测表读数，作为管网漏损节点定位的计算数据．

上述 2套实验方案依次为分步优化模型中的摩阻系数校核和漏损节点定位2个步骤提供了实验数据．而在联合优化模型中，由于摩阻系数校核和漏损节点定位在同一模型中完成，所以只需要在保证6个大用户节点稳态运行的前提下，分别逐点开启6个模拟漏损节点即可直接进行漏损定位．

2 结果与分析

2.1 分步优化模型的管网摩阻系数校核与漏损定位结果

根据第 1.3节中提出的分步优化模型，采用第1.6节中的实验方案和第1.5节中的PSO算法求解方法进行管网模型的摩阻系数校核．摩阻系数校核计算中，PSO算法的粒子数按照一般问题选择20个粒子；粒子的位置上下限在本文中就是摩阻系数的上下限，实验管网材质为镀锌钢管，按照海曾-威廉公式摩阻系数的范围，取粒子位置的上下限分别为 150和100；学习因子取C1＝C2＝2；最大循环数取200．

选取主要管段摩阻系数计算结果列于表 1，考虑到实验管网规模小且管段均为同时期建设，因此可将所有管段摩阻系数视为相同从而简化计算，校核后的摩阻系数和实验测定摩阻系数的对比结果列于表2.

采用表 2中简化计算校核后的摩阻系数，运用PSO算法对实验中的 6个模拟漏损管段进行节点定位．定位计算中PSO算法的具体参数设置如下：粒子数选为 20，粒子位置上下限分别取 1和 61，学习因子取C1＝C2＝2，最大循环数取 200.

2.2 联合优化模型的管网摩阻系数校核与漏损定位结果

根据第 1.4节中提出的联合优化模型，采用第1.6节中的实验方案和第1.5节中的PSO算法求解步骤，同步进行管网模型摩阻系数校核和漏损定位．PSO算法的具体参数设置如下：粒子数选为 30，粒子上下限位置分为2组分别对应于管网摩阻系数和节点编号，学习因子取 C1＝C2＝2，最大循环数取300．最终的漏损定位结果见表3.

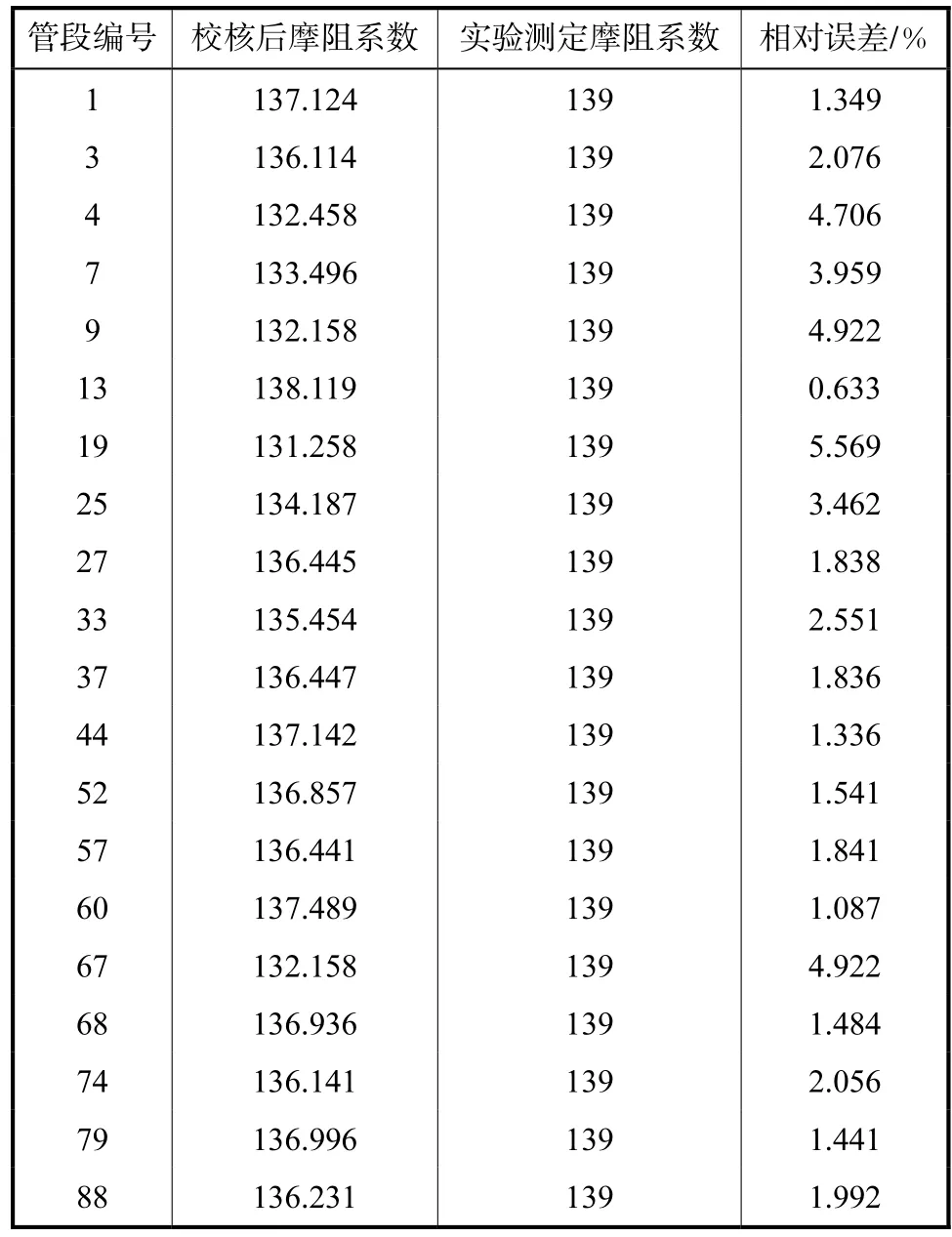
表1 主要管段摩阻系数计算结果Tab.1 Calculation results of the friction resistance coefficient of main pipes

表2 简化计算结果Tab.2 Results of the simplified calculation

表3 2种模型管网漏损节点定位简化计算结果比较Tab.3 Leakage localization results contrast of two models

由表 3可以看出，在联合优化中，在同一管网中漏损定位结果的精度普遍达到相差1环、两根管段甚至同一环中相差1根管段，而分步优化的定位结果则普遍相差2环，因而联合优化的最终定位结果更为准确，这同时表明不同程度、不同位置的漏损对管网的整体水力计算产生了影响．然而，并非联合优化的所有模拟漏损情况下摩阻系数的校核均优于分步优化，这主要是由于联合优化是达到摩阻校核与漏损节点定位的双重优化，相较于单一优化摩阻系数优化势必会在某些计算环节达不到更高的精度，同时算法参数的选择也对计算结果有着重要的影响．因此，如果在条件许可的情况下，尽量采用实际测定的管网参数值会更有利于进行漏损定位的计算．

3 结 论

(1) 本文以实验管网为研究对象，首先针对供水管网的摩阻参数校核和漏损节点定位 2个问题独立建模，提出了分步优化模型，然后将供水管网摩阻系数的校核与漏损节点的定位放在同一模型中，提出了联合优化模型，并针对2种模型的特点制订了相应的实验方案．为求解上述 2个优化模型，尝试使用 PSO优化算法作为求解方法，并在 VC++6.0环境下调用EPANET过程编程实现该算法．最终漏损定位结果表明，PSO优化算法求解本优化模型快速而准确，而且将摩阻系数校核与漏损定位放在同一优化模型中进行联合优化时，漏损节点的定位效果要优于分步优化的最终定位效果．

(2) 在实际管网中，由于压力监测点的数量、布设位置都难以达到实验室条件，且管网节点流量等参数也不容易准确获知，因而应用本研究中的漏损定位方法还难以完全解决实际管网漏损定位问题．如何运用本文的方法结合其他手段对实际管网进行漏损定位是后续研究的方向．

［1］ 余蔚茗，李树平. 基于水量平衡的管道漏损分析[J].给水排水，2008，34(4)：116-119.

Yu Weiming，Li Shuping. Water loss analysis based on water balance model[J].Water and Wastewater Engineering，2008，34(4)：116-119(in Chinese).

［2］ Pudar R S，Liggett J A. Leaks in pipe networks[J].Journal of Hydraulic Engineering，ASCE，1992，118(7)：1031-1046.

［3］ Vitkovsky J P，Liggett J A，Simpson A R，et al. Optimal measurement site locations for inverse transient analysis in pipe networks[J].Journal of Water Resources Planning and Management，ASCE，2003，129(6)：480-492.

［4］ Wang X，Lambert M F，Liggett J A，et al. Leak detection in pipelines using the damping of fluid transients[J].Journal of Hydraulic Engineering，ASCE，2002，128(7)：697-711.

［5］ Kapelan Z，Savic D A，Walters G A. Optimal sampling design methodologies forwater distribution model calibration[J].Journal of Hydraulic Engineering，ASCE，2005，131(1)：190-200.

［6］ Kapelan Z，Savic D，Walters G．A hybrid inverse transient model for leakage detection and roughness calibration in pipe networks[J].Journal of Hydraulic Research，2003，41(5)：481-492.

［7］ 张宏伟，王晨婉，牛志广，等．城市供水管网物理模型构建方法[J].天津大学学报，2008，41(7)：859-863.

Zhang Hongwei，Wang Chenwan，Niu Zhiguang，et al.Constructing method for the physical model of municipal water distribution system[J].Journal of Tianjin University，2008，41(7)：859-863(in Chinese).

［8］ 张利彪，周春光，刘小华，等. 粒子群算法在求解优化问题中的应用[J]. 吉林大学学报：信息科学版，2005，23(4)：104-108.

Zhang Libiao，Zhou Chunguang，Liu Xiaohua，et al. Application of particle swarm optimization for solving optimization problems[J].Journal of Jilin University：Information Science Edition，2005，23(4)：104-108(in Chinese).