长寿风险的识别与量化研究：来自中国的数据

李志生，吕勇斌，刘恒甲

（中南财经政法大学 金融学院，武汉430073）

0 引言

随着生活水平的提高和医疗条件的改善，人类寿命不断延长。据世界卫生组织的统计，2005年我国大陆居民人均寿命为72.4岁，较2000年的70.8岁提高了1.6岁，据预测，到2050年我国大陆人均寿命将超过85岁。寿命的延长一方面提高了退休生活的成本，另一方面也加大了退休金准备不足的风险。

退休计划中决策者主要面临两类风险：第一是财务风险，主要发生在退休金的积累过程，这类风险可能使投资于各类金融资产的财富部分甚至全部损失。一般来说，因健康和通胀等因素的影响，退休者退休后的年均生活费用会显著增加，这使退休生活需要越来越多的财富支撑，如果市场陷入连续滞涨或衰退，退休金将面临巨大的给付压力。第二是长寿风险。寿命的延长本来是人类社会进步的一种表现，但是在人类寿命延长过程中也出现了一个引人担忧的现象，即在生命的最后1/5阶段，即使没有疾病的影响，也往往不同程度地存在生活质量下降的趋势。造成这种现象的主要原因是寿命延长了而工作时间并没有相应延长，这使人们退休后无收入或者低收入生活的年限越来越长。针对这种现象，经济学家引入了长寿风险的概念来表示因寿命过长而导致的退休金准备不足的风险。

虽然长寿风险已经受到国内外学者的广泛关注，但目前学者们关于长寿风险的讨论还局限在定性的层面上，在定量计算方面还没有系统的研究成果。本文借用健康经济学和寿险精算领域中广泛使用的Lee-Carter死亡率模型，并结合经典的下方风险计量方法，探讨退休计划中长寿风险评价的一般方法和定量计算矩阵。本文的研究成果将为年金产品定价、养老年金经济价值的分析、各类养老计划的财务安全和可持续发展问题提供参考。

1 长寿风险的识别与度量

根据Richard（2006）的定义，长寿风险是指由于个人或总体人群未来的实际寿命高于预期寿命而产生的财富短缺风险。基于上述定义可以发现，长寿风险主要来自两个方面：一是由于人口死亡率下降而带来的寿命增加；二是个人或社会群体自身财富效用的变化。一般来说，现实生活中消费者会根据自己的收入状况来安排生活消费支出和投资决策。但是，在目标消费函数确定的情况下，财富总量在退休之后不断减少的趋势可能使目标消费无法满足。因此，对长寿风险的识别需要同时考虑实际寿命高于预期寿命和财富效用短缺这两种可能性。

1.1 死亡率模型

为了度量长寿风险的大小，首先需要对人口死亡率的现状和未来变化趋势进行合理的估计。死亡率数据最直接的来源是人口调查统计结果和保险业经验生命表，但是前者反映的只是死亡率的历史状况，不能直接用来对死亡率进行预测，后者则是源于参保人的经验数据，并不具有广泛的代表性。本文选择被学者们广泛应用的Lee-Carter模型对死亡率进行预测。

Lee-Carter模型的主要思路是将死亡率的变化分解为时间因子t和年龄因子x。如果用mx,t表示时间t时年龄为x岁的人群的中心死亡率，那么mx,t满足以下函数关系：

其中αx为依赖于年龄因子的参数，反映特定年龄人群死亡率自然对数的平均水平；kt为依赖于时间因子的参数，通常称为死亡率指数（Mortality Index），反映死亡率随时间变化的速度；βx表示年龄因子对kt的敏感度；εx,t是均值为0、方差为的误差项。李志生、刘恒甲（2010）利用1992～2007年中国人口分年龄组死亡率数据对Lee-Carter模型进行了估计，并得出了最优的拟合模型。

1.2 长寿风险度量模型

本文构建的长寿风险量化模型如下：

其中，LRx,t表示当前年龄为x岁的人群第t年所面临的长寿风险的大小，Fx,t表示x岁的人群在第t年的存活概率（Fx,t=1-mx,t），Pr o(Ut＜0)表示财富效用小于0的概率。

式（2）中的财富演化函数Wt可以进一步表示为：

其中α为财富的自然增长率，假设其服从正态分布；y是一个服从泊淞分布的参数，代表每年由于意外事件（如重大疾病和自然灾害）的发生而产生的额外支出的次数；Pt表示意外事件发生而产生的额外费用；It为其他收入所得，如社会养老福利和年金福利等；Ct为第t年的目标消费额，包括生活消费、医疗和其他常规支出，其大小由第t－1年的目标消费额Ct-1和居民消费价格指数（CPI）决定。

为了简化分析，这里采用直线效用函数，即假设Ut=Wt。通过分析可以看出，当财富量Wt小于0时，将产生财务风险。通过式（3）获得年龄为x岁的人群未来各年的财富水平，并结合式（1）来获取相应的死亡率数据，便可对未来长寿风险发生的概率进行模拟计算。

理论上，长寿风险发生的时间是退休计划、年金条款以及养老保障制度设计的关键因素，因此在既定的消费目标和其他约束条件下，对长寿风险首次发生时间的估计有着重要意义。通过改变模型中各参数的取值，并模拟计算不同参数取值下的结果，可以进行相应的敏感性分析，以检验模型中各个参数对长寿风险的影响方向和程度的大小。这将有利于加深对长寿风险的认识，更好地制定出应对和管理长寿风险的方法和工具。

2 数值计算

根据第1部分提出的长寿风险度量模型，本部分对不同参数设置下的长寿风险进行模拟计算，并就各参数对长寿风险的影响进行分析。

2.1 算法构建

模型（2）对LRx,t的计算涉及到时间和年龄两个维度，同时还需考虑年龄X随时间t的变化。本文将实际寿命超过预期寿命情况下财富短缺的可能性定义为长寿风险。基于李志生、刘恒甲（2010）的研究，2011年我国新生人口的期望寿命为75岁，为此我们以未来24年（t=1…24）75～99岁人口死亡率预测值和财富演化路径两个参数来实现对长寿风险的模拟，模型（2）可简化为：

模型（4）将年龄和时间两个维度的参数结合为单一参数在一定程度上简化了计算。模型（4）得到的长寿风险是一个相对指标，表明在未来24年里75～99岁各年龄的人群面临长寿风险的概率。模型（4）的仿真和模拟计算可经过以下几个步骤完成：

第一步：使用Lee-Carter模型获取未来不同年份不同年龄组人口的死亡率预测值，并将分年龄组人口死亡率分解为各岁数人口的死亡率；

第二步：根据影响财富效用函数（3）的四个因素设定若干组参数，并计算每组参数设置下的目标消费函数和财富效用函数的演化路径；

第三步：从60岁年龄分组开始，判断效用函数Ut是否小于0，当Ut＜0时，即认为在t年60＋t岁的人群将面临财务风险；将60＋t与期望寿命75岁进行比较，如果60＋t＞75，则认为存在发生长寿风险的可能性；

第四步：在特定的参数设置下，对模型（4）进行N次模拟计算，并对第三步识别出的长寿风险发生时间点t时的Ut＜0做出统计，并以此计算第t年长寿风险发生的概率。

2.2 长寿风险的模拟计算和分析

我们用一年期国债来近似代表财富的自然增长率，过去十年我国一年期国债的平均利率为3.7%，标准差为15%；意外事件发生的次数y服从泊淞分布，即Pr o(y=k)=e-λλk/k!，我们假设意外事件发生的频率为10%；因意外事件发生而产生的额外费用Pt为0.5倍的当期消费，即Pt=0.5Ct；It为0，即假设退休后不存在其他收入；初始财富为10个单位，消费额Ct-1为0.6个单位。为了分析不同参数的变化对长寿风险首次发生时间的影响和长寿风险首次产生的概率的影响，我们设置以下五组参数。

表1中，第二组模拟计算改变了参数Ct-1，以考察目标消费与长寿风险的关系；第三组模拟计算改变了参数μ，以考察财富增长率对长寿风险的影响；第四、五组模拟计算分别改变了σ和λ，以考察财富增长的波动率和意外事件发生的频率与长寿风险的关系。

针对表1的每组参数，我们分别对模型（3）进行2000次模拟计算，并计算出当年发生财富效用短缺的概率，结果如图1所示。

从图1可以看出，当参数Ct-1从0.6减小到0.3时，在75岁之前发生财富短缺的概率大幅度降低；当财富平均年增长率μ从3.7%增加到6%时，在73岁之前发生财富短缺的概率普遍降低；当财富增长的波动率15%增加到了30%时，短期内发生财富短缺的概率显著增加；当意外事件发生的概率增加到20%（即平均每5年发生一次意外事件）时，短期内发生财

表1 五组模拟计算中模型参数的设置

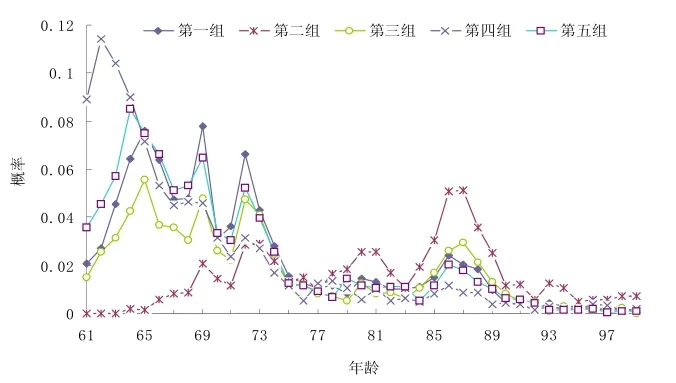
图1 首次发生财富短缺的概率

图2 首次发生长寿风险的概率

3 结论与建议

本文在对长寿风险进行定性分析的基础上，提出了一个定量化的长寿风险度量模型，并根据相关数据对未来人口的长寿风险进行了模拟计算。结果显示目标消费量、财富增长率的均值与方差、意外事件发生的频率等参数对长寿风险发生的时间及其概率分布有较大影响。

人类寿命的延长本身是社会进步的一种表现，但是如果社会不能提供足够的财富来维持寿命延长所带来的更多消费支出，社会个体退休后的生活水平将会出现大幅度的下降，进而产生严重的社会问题。欧美发达国家的人口老龄化是伴随着城市化和工业化的进程而出现的，也就是说经济高度发达和人口结构转变是同时发生的。而在我国，2005年60岁以上的人口已占总人口的11%，并且这一比例将在本世纪中叶超过30%，但届时我国人均GDP和经济发展质量只能达到中等发达国家水平。“未富先老”的现实，加之庞大的人口基数，使得长寿风险日益成为一个亟待解决的新的社会问题。对于如何应对人口老龄化所带来的长寿风险，结合本文的分析结果，我们提出以下几点建议：

（1）重视不同社会群体长寿风险的区别

从第2章中五组参数的不同计算结果来看，不同参数设置下长寿风险发生的时间点和概率大小都存在明显差别。当然还有更多影响长寿风险的因素需要我们识别和研究。识别这些不同的影响因素，划分不同的社会群体，了解不同社会群体在面临长寿风险时的财务状况显得尤为重要。

居民收入分配不均和地区经济发展不平衡等导致贫富分化加重的现象，使得不同的社会群体在财务安全感和稳定感上存在很大差别。社会保障体系特别是农村保障体系的不完善和低水平，直接导致这部分人群有可能面临较为严重的长寿风险。同样，长寿风险的差别存在于公务员、自由职业者、运动员、教师、私营经济者和农民等不同职业者之间，以及富短缺的概率也明显增加。

接下来我们根据式（4），对表1的每组参数分别进行2000次模拟，得到长寿风险发生概率，如图2所示。

我们发现，75岁之后长寿风险的发生几乎是必然的，但是在不同年龄长寿风险发生的概率有所不同。对于不同的参数设置，长寿风险首次发生在85～88岁之间的概率最大，首次出现在90岁以上的概率很小（小于1%）。此外，平均财富增长率、财富增长的波动率、目标消费量以及意外事件发生的频率都在一定程度上影响着长寿风险首次发生的时间及其概率。东西部等地区之间等。因此如何识别不同社会群体所面临的长寿风险发生的时间点和概率大小是一个重要的研究课题。

（2）转嫁和对冲长寿风险的金融产品的开发和使用

根据国家人力资源和劳动保障部公布的数据，截至2009年底，全国参加城镇基本养老保险、基本医疗保险和失业保险的人数为2.35亿、4亿和1.27亿。也就是说我国人口当中有近70%的人口未能纳入养老保险体系当中，这一方面说明我国人民的各项社会保障还处于很低的水平，覆盖面非常有限，同时也说明针对长寿风险的金融产品将存在广阔的市场空间，比如年金产品、寿险产品和证券化产品等。

养老年金的经济价值在理论界得到了广泛的肯定，但实际经济数据却显示，养老年金并不被很多人接受，即使是在年金市场较为发达的美国，年金的购买比例和年金化率都很低。因此针对长寿风险，如何充分发挥养老年金的重要作用将是一个重要的研究课题。

此外，金融市场的创新性和风险转移能力可以为长寿风险管理提供新的方式与渠道。发挥金融市场创造性和风险转嫁功能，为长寿风险的规避提供金融工具也具有积极的现实意义。

[1]Anderson,Artbur W.Pension Mathematics for Actuaries[M].American:The Windsor Press Inc,1985.

[2]Antolin Pablo.Longevity Risk and Private Pensions[C].OECD Working Paper on Insuranceand Private Pensions,No.3，2007.

[3]Brouhns,N.,Denuit,M.,Van Keilegom,I.Bootstrapping the Poisson log-bilinear Model for Mortality Forecasting[J].Scandinavian Actuarial Journal，2005,（3）.

[4]Brouhns,N.,Denuit,M.,Vermunt,J.K..Measuring the Longevity Risk in Mortality Projections[J].Bulletin of the Swiss Association of Actuaries,2002，（2）.

[5]Lee R.D.The Lee-Carter Method for Forecasting Mortality,with Various Extensions and Applications[J].North American Actuarial Journal，2000,4(1).

[6]Li,N.,Lee,R.,Tuljapurkar,S.Using the Lee Carter Method to Forecast Mortality for Population with.Limited Data[J].International Statistical Review,2004,72(1).

[7]Steinmann Lukas,Scotti Veronica.Annuities:Private Solutions of Longevity Risk[J].Sigma,2007,(3).

[8]Stanley R.Pliska,Jinchun Ye.Optimal Life Purchase and Consumption、Investment under Uncertain Lifetime[J].Journal of Banking and Finance,2007,(10).

[9]陈秉正，祝伟.长寿风险管理研究综述[R].北大CCISSR(赛瑟)论坛，2008-4-10.

[10]李志生，刘恒甲.Lee-Carter死亡率模型的估计与应用——基于中国人口数据的分析[J].中国人口科学，2010,(3).