管网叠压供水系统自抗扰控制

李洪凤，陈浈斐，柴秀强，陈 炜

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津甘泉集团有限公司，天津 300352)

管网叠压供水采用变频调速技术，直接将水泵串联到市政管网上，再经加压后送至各用水点．系统充分利用了管网余压，节省了能源，且无需蓄水设备，避免了水质的二次污染[1]．但是管网叠压供水系统受到市政管网余压和用户流量的双重干扰，系统的工作点变动较大，使得该系统控制起来比较困难[2]，如果控制不当则会直接影响市政管网系统和周围用户的用水．水泵工况的非线性改变以及各种不确定的扰动，使得叠压供水系统难以建立精确的数学模型．文献[3]在模型中考虑了电价变量，对供水系统采用预测控制．文献[4]在对供水系统的参数进行动态辨识的基础上对其采用自适应控制．目前，实际控制系统中采用最多的是常规PID控制．然而，常规PID控制由于参数不可调节，虽然能够保证供水压力静态偏差基本达标，满足用户用水的流量需求，却不能顾及调速过程的动态特性，供水动态品质较差．如果调节不当，则会使供水过程中压力振荡幅值过大，引发供水管路振荡、水流喘振等多种不良状态，对管网造成损坏，且影响到供水稳定性及用户的用水舒适性．

自抗扰控制技术继承了常规 PID控制不依赖控制对象具体数学模型的特点，是一种基于过程误差的非线性调节方式，适用于外部扰动因素较强、被控对象时滞性大且对控制效果动态特性要求较高的控制系统，算法简单，易于实现，具有较高的工程实用价值[5-6]．目前，自抗扰控制已在电机控制、火电厂单元机组协调、电力电子变换器控制等多项实际工程中获得应用[7-9]．笔者对管网叠压供水系统采用自抗扰控制技术进行控制，通过仿真可以看出管网叠压供水系统采用自抗扰控制器后，具有较好的动态特性、鲁棒性能和抗干扰能力．

1 叠压供水系统

1.1 管网叠压供水系统结构

管网叠压供水系统的结构如图1所示．

图1 叠压供水系统原理Fig.1 Principle of pressure-superposed water supply system

图 1中，管网叠压供水系统主要由稳压罐、负压消除器、压力传感器、变频控制器和 PLC中心控制单元组成．其设备进水管接到市政供水管网上，自来水经过倒流防止器进入稳压罐中，稳压罐为一承压罐，起到少量蓄水和稳压的作用．负压消除器可根据稳压罐内的压力自动启闭，平衡稳压罐内的压力避免产生负压．PLC中央控制单元根据压力传感器测得的扬程偏差，控制变频器调节异步电动机的转速，使水泵扬程达到要求．

1.2 管网叠压供水系统数学模型

叠压供水系统中被控对象主要包括变频器、异步电动机和水泵．变频器数学模型为

变频器在恒压频比控制方式下工作，即E1/f1为常数，则异步电动机气隙磁通φm保持恒定不变．则异步电动机旋转时的转子感应电势为

电动机旋转时，转子回路电流稳态值为

式中：R2为转子回路电阻；X2σ为转子回路对应频率等于f1时的漏电抗．

在变频调速过程中，由于转子回路存在电磁惯性，转子电流的动态过程可等效成一阶惯性环节[10]，即

式中 τa为异步电动机转子回路惯性时间常数，τa＝L2σ/R2，L2σ为转子回路电感．

由转子电流I2可推知异步电动机的电磁转矩为

将式(3)和式(4)代入式(5)可得

式中：Cm=为电磁转矩常数；p为异步电动机极数；I2cosφ2是转子电流的有功分量；F1(s)为 f1的拉普拉斯变换式．

异步电动机输出电磁转矩Tem、负载转矩Tf和异步电动机转速n三者之间的关系为

式中 GD2为系统总飞轮矩．在叠压供水系统中，水泵作为异步电动机的负载通过联轴器与电动机相连．负载转矩 Tf主要受到水压和用户流量 Q等因素的影响．由于用户流量无法预知，这里将异步电动机负载转矩Tf看成系统干扰w1．

式中N(s)为异步电动机转速n的拉普拉斯变换式．

将式(6)代入式(8)中，可得

式中 sm与电动机转速n 和f1都有关，可见n与控制量f1之间存在耦合，系统为非线性系统．

图2 自抗扰控制器结构Fig.2 Structure of ADRC

根据比例定律，水泵扬程H与异步电动机转速n的二次方成正比．

式中：n为异步电动机转速；ne为水泵工作在额定状况下异步电动机的转速；H 为水泵的扬程；He为水泵额定工况下的扬程．

在叠压供水系统中，系统输出扬程除了水泵的净扬程外还叠加了管网余压 H0．因为管网余压的大小不能确定，可将其对系统变量的影响看成为系统干扰w2．则整个系统简化的数学模型可等效为

2 自抗扰控制器

自抗扰控制下的管网叠压供水系统结构如图 2所示．

图 2中，自抗扰控制器主要由 4个部分组成：基于非线性跟踪微分器(TD)安排的过渡过程、扩张状态观测器(ESO)、非线性组合(NLSEF)和扰动补偿．v(t)为根据用户根据楼层高度设定的水泵输出扬程参考值．

非线性跟踪微分器不仅可以安排过渡过程，而且能够解决系统快速和超调之间的矛盾，提供参考值的各阶导数．其表达式为

其中，非线性函数取为

跟踪微分器解的分量 z11在加速度限制 d2z11/dt2＜R1的限制下，最快速度地跟踪输入信号 v(t)，且参数R1值越大，跟踪速度越快．z12为z11的导数．

扩张状态观测器用来观测系统状态变量及其各阶广义微分信号．表达式为

式中：y为系统变量；z21、z22分别是对系统中状态变量的估计；z23是扩张状态变量，它能估计出作用于系统的加速度的实时作用量，并将系统未知部分和外界扰动一起归结为系统的总扰动进行估计；非线性函数为

非线性组合通过配置非线性函数对系统实施前馈补偿，较线性反馈具有更好的干扰抑制能力．其表达式为

扰动补偿部分将非线性函数得到的反馈控制量u0用扰动估计值z23进行补偿，最终得到控制量u．

在本系统中，要得到扰动补偿的系数，需将式(13)转化到时域中，为

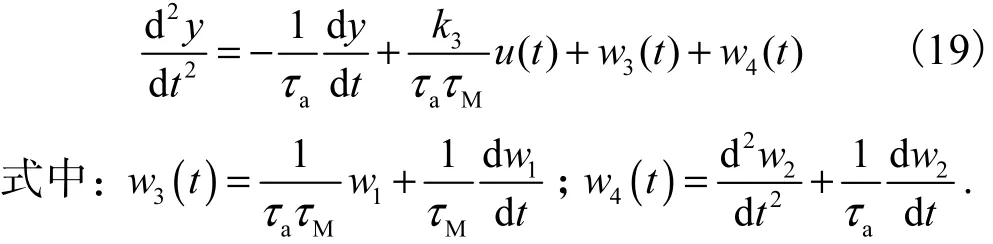
令 b＝k3/τaτM，因 k3与 sm有关，所以 b 不为常数．但是由于本系统中采用变频调速控制，sm稳态状态下变化范围很小，一般在 0.02～0.05之间．取异步电动机额定工作情况下的 sm计算 k3的估计值，记为常数K*．

3 仿真结果与分析

根据图2和自抗扰控制器的原理在Simulink里建立管网叠压供水系统的仿真模型，如图3所示．

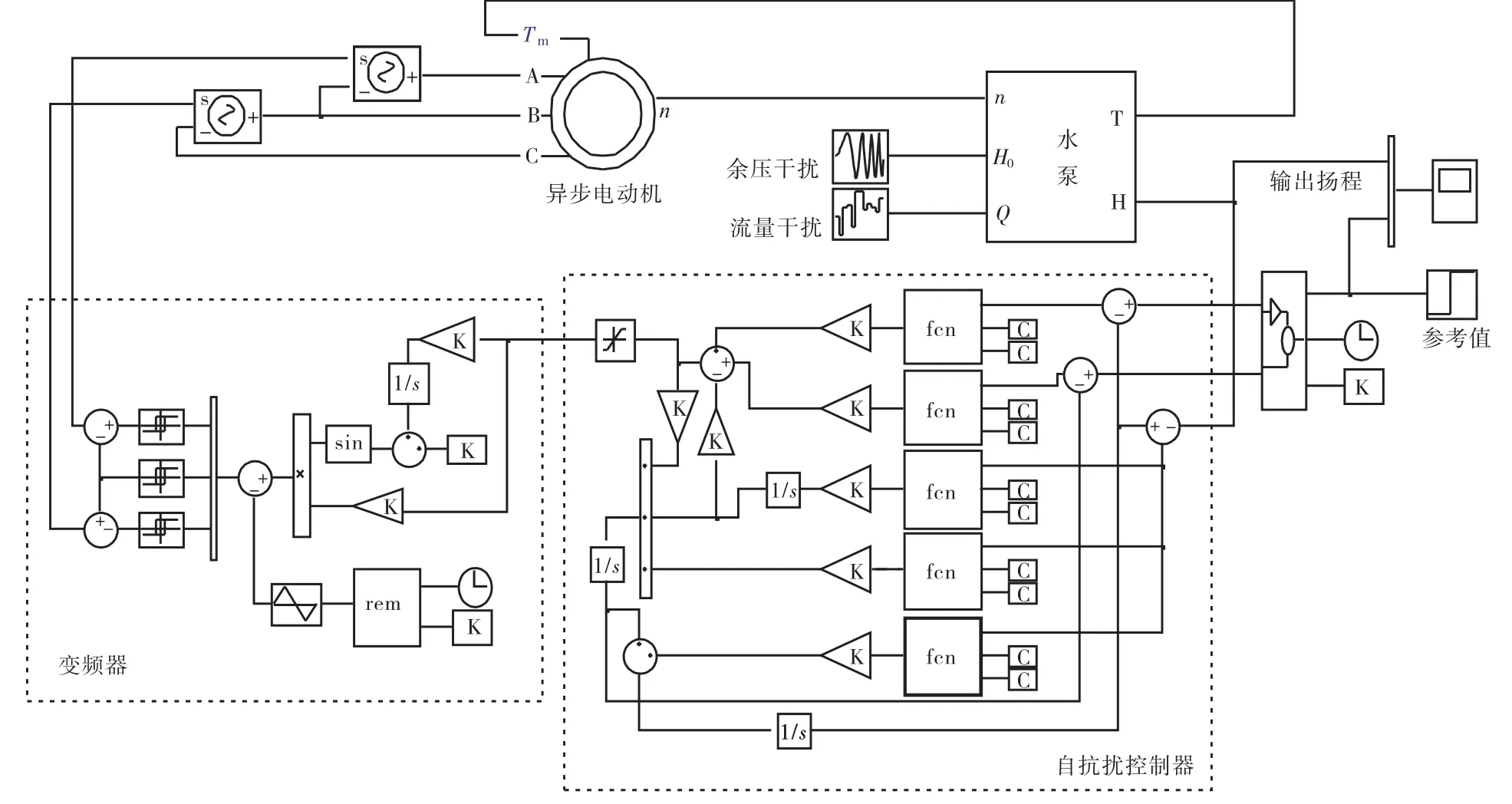
图3 系统自抗扰控制器仿真模型Fig.3 Simulation model of system with ADRC

对于某管网叠压供水系统，其异步电动机参数为PN＝15,kW，p=2，NN＝1,460,r/min，额定电压 UN＝400,V，频率 fN＝50,Hz，定子电阻 Rs＝0.214,7,Ω，定子电感 Ls＝0.000,991,H，转子电阻 Rr＝0.220,5,Ω，转子电感 Lr＝0.000,991,H，互感 Lm=0.064,19,H，惯性常量J＝0.102,kg·m3，摩擦因子 F=0.009 54,N·m·s．

当系统工况为 H0＝5,m，q=20,m3/h时，分别对其采用常规PID和自抗扰控制器进行控制．通过调整2种控制器的参数，使其都达到最佳效果，此时常规PID 参数为 Kp＝50、Ki=3、Kd＝0.5，自抗扰控制器参数为 R1=600、β01＝4,000、a01=0.5、β02＝200、a02=0.5、β1＝50、a1=0.75、β2＝3,000、a2=0.5、β3＝4,000、a3=0.5、δ＝0.01、b0=200．

当扬程参考值由32,m突变到40,m时，系统的响应曲线如图4所示．

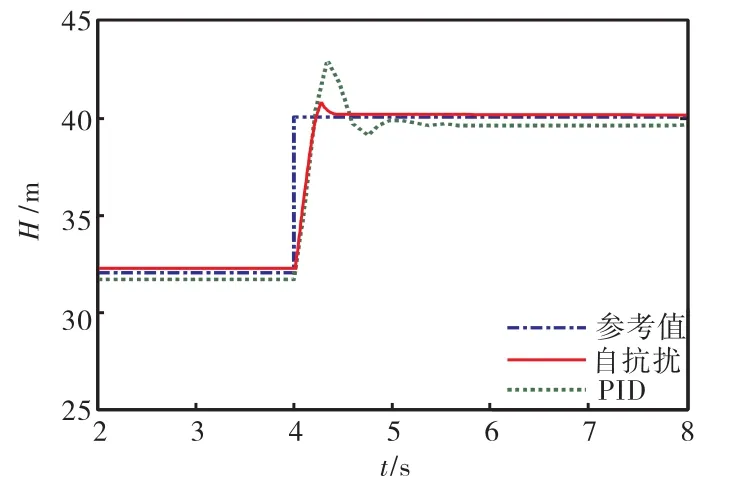
图4 阶跃输入时的响应曲线Fig.4 Response curves based on step input

由图 4中可以看出，当扬程发生阶跃变化时，与常规PID控制相比，自抗扰控制加快了系统的响应速度，降低了系统响应的超调，稳态精度也得到了提高．可见自抗扰控制器改善了系统的动态性能．

为比较 2种控制器对不同工况的适应范围，保持2种控制器的参数不变，当用户流量 q＝10,m3/h时，得到该系统对2种控制器的响应曲线如图5所示．

图5 轻载时系统响应曲线Fig.5 Response curves with light load

由图5可以看出，水泵负载变小后，常规 PID不仅超调增大，而且稳态时的波动也比较厉害，而自抗扰控制器的控制效果基本不变．由此可见，自抗扰控制器对被控对象的模型精度要求不高，适应范围更广，鲁棒性更强．

管网叠压供水系统在运行时受到市政管网余压和用户流量的双重干扰．当在市政管网余压发生阶跃变化时，H0由5,m突变到10,m，系统在2种控制器控制下的响应曲线如图6所示．

图6 受管网余压扰动后响应曲线Fig.6 Response curves with pressure interference

由图 6可以看出，在相同的管网干扰下，自抗扰波动较小，调节时间较短，比常规 PID的抗干扰性能更好．

当在用户流量发生阶跃变化，q由 10,m3/h突变到 20,m3/h，系统在 2种控制器控制下的响应曲线如图7所示．

图7 受用户流量扰动后响应曲线Fig.7 Response curves with flow interference

由图 7可以看出，由于用户流量变化，引起了水泵转矩和功率变化，系统在2种控制器控制下均出现了一定稳态误差．相比之下，自抗扰的稳态误差较小，鲁棒性能更强．

4 结 语

对于管网叠压供水系统，自抗扰控制器不仅可以安排过渡过程，解决了超调和快速的矛盾，得到系统变量的微分值，而且可以有效观测出系统的扰动并加以补偿，具有很强的抗干扰性能．本文建立了叠压供水系统的 Simulink仿真模型，分析了在市政管网余压和用户流量干扰下系统运行的情况，通过仿真分析可知自抗扰控制器比常规 PID控制器抗干扰能力更强，适应范围更广，具有很好的鲁棒性，更适应管网叠压供水系统．

［1］潘书通，张 斌，孙建民. 直接管网叠压供水设备的工作原理与应用[J]. 给水排水，2003，29(12)：70-72.

Pan Shutong，Zhang Bin，Sun Jianmin．The principle and application of pressure-superposed water supply in direct pipe network[J].Water and Wastewater，2003，29(12)：70-72(in Chinese).

［2］樊建军，魏晓安，王 峰. 管网叠压供水技术存在的主要问题及解决途径[J]. 中国给水排水，2006，22(22)：39-42.

Fan Jianjun，Wei Xiaoan，Wang Feng．Problems in network pressure-superposed water supply system and corresponding solution[J].China Water and Wastewater，2006，22(22)：39-42(in Chinese).

［3］Azenic B，Peric N，Sliskovic D. Predictive control of water supply plant[J].Electronics，Circuits and Systems，2002，2(1)：653-656.

［4］Man K F，Yung W K，Chow T W S. Adaptive control strategy for a water supply system[C]//Third International Conference on Software Engineering for Real Time System.Cirencester，UK，1991：125-128.

［5］Han Jingqing. From PID to active disturbance rejection control[J].IEEE Transactions on Industrial Electronics，2009，56(3)：3428-3429.

［6］Sun Dong. Comments on active disturbance rejection control[J].IEEE Transactions on Industrial Electronics，2007，54(6)：900-906.

［7］Xia Y，Shi P，Liu G P，et al. Active disturbance rejection control for uncertain multivariable system with timedelay[J].IEEE Control Theory Appl，2007，1(1)：75-81.

［8］Su Y X，Zheng C H，Duan B Y. Automatic disturbances rejection controller for precise motion control of permanent-magnet synchronous motor[J].IEEE Transactions on Industrial Electronics，2005，52(3)：814-823.

［9］Martini A， Leonard F，Abba G. Robust nonlinear control and stability analysis of a 7DOF model-scale helicopter under vertical wind gust[C]//Intelligent Robots and Systems. Nice，France，2008：354-359.

［10］孙铁成，郎永强，李 冰，等. 异步电动机简化模型的建模方法[J]. 控制工程，2003，10(增)：50-51，148.

Sun Tiecheng，Lang Yongqiang，Li Bing，et al. Simplified model of asynchronous motor[J].Control Engineering of China，2003，10(Suppl)：50-51，148(in Chinese).