基于GIS的区域经济统计分析模型研究及应用——以江西省为例

李恒凯，刘小生，陈优良

(江西理工大学建筑与测绘工程学院，江西赣州341000)

0 引言

GIS作为一种交互式的、可视化的决策支持工具，和传统分析方法一样，在区域统计分析中发挥着重要的作用。近年来，不少学者致力于空间统计学与GIS的结合以及其在社会经济发展领域的应用研究。鲁凤［1］、席建强［2］、麻清源［3］、陈斐［4］、宋琳［5］将空间相关分析与 GIS进行结合，研究了区域经济的空间集聚特征;王世杰［6］除了采用空间相关分析技术，还采用了相对发展率、锡尔系数和加权变异系数来研究区域经济差异及其演变规律;杜茂华［7］利用锡尔系数和基尼系数对城乡间经济发展差异进行了研究。这些研究为区域经济分析提供了丰富的技术方法，但由于现行的GIS软件在统计分析方面功能较弱，如空间自相关分析、基尼系数计算、回归分析等分析模型还必须借助统计分析软件完成，这使得区域经济统计分析模型与GIS不能紧密集成，增加了这些技术方法的使用难度并限制了其广泛应用。在这些研究基础之上，本研究以GIS作为数据管理和模型集成平台，采用完全一体化的集成方式，对区域经济分析中常用的统计分析模型利用GIS进行重新构建，并基于这些模型，开发出了基于GIS的区域经济统计分析系统，为区域经济的统计分析提供了实用的技术方法。

1 区域经济统计分析模型建立

1.1 模型建立思路

模型建立如图1所示，首先，利用GIS对区域统计单元的人口经济数据和统计单元地图数据进行图形属性一体化管理，人口经济数据主要存储各个统计单元历年人口数据和历年的GDP数据，进而获得各统计单元历年人均GDP数据。利用统计单元的地图数据，结合GIS的分析功能，方便得到各个统计单元的相互邻接关系的权重矩阵。利用权重矩阵和各统计单元历年人均GDP数据，可计算区域人均GDP的空间自相关指数，得到区域全局和局部自相关指数，并以GIS专题图形式进行直观显示，了解人均GDP的空间集聚情况。可以对区域人口数据和GDP数据进行相关分析，以了解人口对GDP的影响情况。通过区域历年的人均GDP数据，可以对这些数据进行集中化与均衡度分析，包括基尼系数分析、相对发展率分析、集中指数分析、变异系数分析，以从不同角度了解整个区域经济发展状况。

图1 模型建立逻辑示意图Fig.1 Logic schematic diagram of model establish

1.2 集中化与均衡度分析模型建立

为了揭示经济现象分布的基本格局，常常需要计算相关经济数据分布的集中化与均衡度指数，本模型采用人均GDP数据，利用多种方法从多角度对其进行计算，具体如下。

1.2.1 基尼系数。本模型利用基尼系数来分析各个区域间人均收入分配的差异状况。其计算方法为:首先，通过区域统计单元历年人口数据和GDP数据，得到各个区域统计单元历年的人均GDP数据。然后，对于每一年，分别将区域内各统计单元按人均GDP按由高到低进行排序，按照排序顺序，分别计算人均GDP由低到高的各统计单元GDP占整个统计区域GDP的比重wi，人口占统计区域比重Pi，基尼系数计算公式为

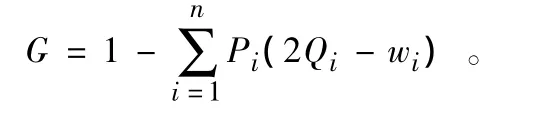
1.2.2 相对发展率。相对发展率表示各统计单元在某一时期内人均GDP的变化与同时期整个区域人均GDP的变化之间的关系［6］，可以准确地反映各个统计单元的发展速度。计算公式为:N=(y2i－y1i)/(y2－y1)。式中:y2i和y1i分别表示i统计单元在时间2和时间1的人均GDP;y2，y1分别表示整个统计区域在时间2和时间1上的人均GDP。

1.2.3 集中化指数。本模型中用集中化指数来定量化地表示统计区域人均GDP分布的集中程度。其指数构造公式为:Ik=(A－R)/(M－R)。式中:Ik表示第k年的区域各个统计单元人均GDP集中指数;A表示各统计单元人均GDP占整个统计区域人均GDP总和的比重按从大到小排序后的累积百分比总和;R表示各统计单元人均GDP均匀分布时的累积百分比总和;M表示各统计单元人均GDP集中分布时的累积百分比总和。

1.2.4 变异系数。本模型中，利用变异系数计算各统计单元人均GDP的相对变化程度。其计算公式为

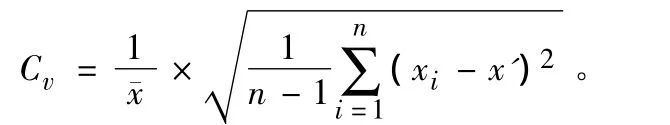
式中:n表示区域统计单元的个数;xi表示第i个统计单元人均GDP数据;x′表示统计区域人均GDP数据。

1.3 相关分析模型建立

相关分析是揭示地理要素之间相互关系的密切程度，主要通过相关系数的计算和检验来完成，相关系数又可细分为:两要素之间的相关系数、秩相关系数、偏相关系数、复相关系数等。其中，秩相关系数r′xy反映了区域人口与经济规模的关系，其计算公式为

式中:r′xy表示秩相关系数;n代表统计单元;R1i表示第i个统计单元在统计区域中人口规模的位次;R2i表示第i个统计单元在统计区域中经济规模的位次。

1.4 空间自相关模型建立

空间自相关性使用全局和局部两种指标，全局指标用于探测整个研究区域的空间模式，使用单一的值来反映该区域的自相关程度;局部指标计算每一个空间单元与邻近单元对某一属性的相关程度。本模型通过计算全局Moran指数和局部Moran指数来度量区域平均GDP数据空间相关性指标。

1.4.1 全局Moran指数I定义如下，即

1.4.2 局部Moran指数Ii定义如下，即

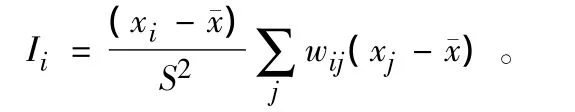
式中:xi，xj分别为第i，j个统计单元人均GDP数据;其他各变量意义同上。若各统计区域之间相邻，则wij为1，否则，为0。在本模型中，空间权重矩阵和GIS图层建立实时的动态链接，通过GIS的拓扑分析功能实现自动维护。全局和局部Moran指数可以用标准化统计量Z来检验n个统计区域是否存在空间自相关关系。

2 模型应用实践

根据以上模型建立思路，以ArcEngine作为GIS软件平台，以C#2008作为编程语言，以SQL Server 2005作为数据库平台，对该区域经济统计分析模型进行了编程实现，并以该模型为基础，开发了区域经济统计分析系统。为验证模型的实用性，以江西省统计年鉴2001—2008年度地级市社会经济数据作为测试数据，运用该系统提供的经济统计分析模型进行了应用实践，下面对分析的具体情况作简要介绍。

2.1 经济的集中化与均衡度

通过运行系统，计算江西省2001—2008年各年度的各地级市人均收入的基尼系数、人均GDP集中化指数和人均GDP变异系数。计算结果如表1所示。从表1可以看出，2001—2008年，江西省各地级市之间的人均收入的基尼系数均在一个正常范围之内，说明江西省的各个地级市人均收入分配是相对比较合理的，但是基尼系数呈逐年递增的趋势，地级市之间人均收入分配差异在变大，贫富差距在拉大，所以，政府部门应该进行必要的宏观调控，避免出现两极分化。2001—2003年，集中化指数是增大的，即集中化程度变大，通过系统查询人均GDP数据可知，人均收入高的地方集中在南昌、景德镇、新余等地区。2003—2008年，该指数呈下降趋势，即集中化的程度变小，各个地区朝比较均衡的方向发展。从表1变异系数可以看出，江西省各市之间的经济发展水平的相对差异基本是增大的趋势，这一变化与江西省宏观经济政策变动的时间大体一致，区域经济政策对地区间经济发展差异的变化有很大影响，个别地区有国家或者省里的政策支持，得到了优先发展的机会，有的地方则相对发展缓慢。通过系统相对发展率计算功能，计算2001—2008年这8年间江西省各地级市相对发展率，得到如表2所示数据。

表1 江西省2001—2008年基尼系数、人均GDP集中化指数和变异系数Tab.1 Gini coefficient，concentration index and the variation coefficient of per capita GDP in Jiangxi Province during 2001—2008

表2 江西省2001—2008年地级市相对发展率Tab.2 The relative development rate of prefecture-level city in Jiangxi Province during 2001—2008

从表2数据可以看出:(1)各地级市相对发展率相差很大，新余最高，赣州最低，两地相差4.5倍，说明省内地级市之间经济发展速度有一定差异。(2)江西省人均GDP的相对发展率N大部分集中在0.6～0.8之间，低于平均水平，从空间位置上，主要分布在江西南部。(3)相对发展率最高的是新余，其次是南昌，遥遥领先于其他各地区，新余是江西工业化程度最高的城市，以新钢为主的钢铁产业和以江西赛维为主的光伏产业有效带动了整个区域的经济发展，南昌作为省会城市和交通枢纽，具有得天独厚的优势。

2.2 人口与经济规模的秩相关分析

运行系统后，进入相关分析模型界面，利用各地区GDP数据与人口数据，计算出了它们之间的秩相关系数。本模型计算出人口与GDP位序秩相关系数为0.781 8，统计单元 n=11，显著水平a=0.01，查表得临界值Ra=0.746，说明江西省各地区人口规模与GDP是等级相关的。

2.3 人均GDP的空间自相关分析

运行系统后，进入空间自相关分析界面，对江西省各地区人均GDP数据进行空间自相关与局部空间自相关指数计算，从而了解江西省各地区人均GDP是否具有空间集聚性及集聚状况，计算出江西省2001—2008年各地区人均GDP的自相关指数(表3)。

表3 江西省2001—2008年全局和局部人均GDP Moran指数Tab.3 Global and local Moran index of per capita GDP in Jiangxi Province during 2001—2008

根据表3数据并进行显著性检验，江西省2001—2008年各地区人均GDP全局Moran指数呈负的空间自相关，说明各地级市2001—2008年人均GDP总体比较分散，没有明显的空间集聚，全局Moran指数有进一步减小的趋势，但总体上基本趋于稳定，说明区域人均GDP分布的空间分布模式变化不大，也说明江西区域经济呈现较均衡的发展。局部Moran指数为正，其对应的统计单元人均GDP数据低于全省人均GDP数据时，空间关联为“低—低”关联，若高于全省人均GDP数据时，空间关联为“高—高”关联;局部Moran指数为负，其对应的区域统计单元人均GDP数据低于全省人均GDP数据时，空间关联为“低—高”关联，若高于全省人均GDP数据时，空间关联为“高—高”关联。由此系统生成关联类型图(图2)。

图2 江西省人均GDP局部自相关关联类型图Fig.2 Local autocorrelation type of per capita GDP in Jiangxi Province

从图2可以看出，江西省局部自相关类型主要为高—低集聚和低—低集聚两种类型，人均GDP高值区分散分布于江西省北部，无明显集聚现象，江西省面积较大的几个地区均为人均GDP低值区，且处于低—低集聚，虽然总体上江西整个区域发展较为均衡，但从图2可以看出，江西省经济发展还是有一定的南北差异，作为省会城市的南昌，并没有发挥省会城市的辐射作用，有效带动周边区域的发展，形成高高集聚。结合表3人均GDP局部自相关系数可知，南昌人均GDP远远高于周边区域，但随着时间推移，南昌局部自相关指数绝对值逐渐减小，说明南昌与周边区域人均GDP差异在减小，南昌逐渐在发挥省会城市对周边区域的辐射作用。值得注意的是，江西省地区经济的低—低集聚有逐渐增强的趋势，需要采取措施，防止区域经济发展的不平衡。

3 结论

将区域经济统计分析模型与GIS相结合，利用后者丰富的空间分析功能和强大的交互功能与可视化功能，能够较好地对区域经济分布利用多种模型从多角度进行分析，为区域经济的统计分析提供了有效的方法，从而为区域政策的制定提供依据。本研究利用GIS技术对传统的区域经济统计分析模型进行了重构，并基于该模型开发了区域经济统计分析的GIS系统。利用该系统对江西省各地区人均GDP的统计分析表明，该区域经济统计分析模型能够有效应用于区域的经济统计分析，方便政府部门制定经济相关决策，具有广泛的应用推广价值。

［1］鲁凤，徐建华.中国区域经济差异的空间统计分析［J］.华东师范大学学报(自然科学版)，2007，46(2):44－52.

［2］席建强，刘超，高小敏.陕西省区域经济增长差异的空间统计分析［J］.统计与决策，2009(4):92－95.

［3］麻清源，马金辉，张超，等.基于交通网络空间权重的区域经济空间相关分析［J］.地域研究与开发，2007，26(5):42－48.

［4］陈斐，陈秀山.局部空间统计在区域经济分析中的应用［J］.华中师范大学学报(人文社会科学版)，2006，45(4):51－56.

［5］宋琳，董春，胡晶，等.基于空间统计分析与GIS的人均GDP空间分布模式研究［J］.测绘科学，2006，31(4):123－126.

［6］王世杰，赵军.基于GIS的甘肃省区域经济时空差异研究［J］.测绘科学，2010，35(2):170－173.

［7］杜茂华，杨刚.基于锡尔系数和基尼系数法的重庆城乡发展差异分析［J］.经济地理，2010，30(5):773－778.