基于兰彻斯特方程的维稳军事行动军械装备维修任务量估算

王开良，史宪铭，于洪敏，杨振军

（1.装备指挥技术学院，北京 101416；2.军械工程学院，河北 石家庄 050003；3.装甲兵工程学院，北京 100072）

0 引 言

反恐维稳，是通过使用军事力量消除恐怖主义威胁，处置突发群体事件，以达成维护社会稳定的政治目的。随着世界局势和国内外政治日趋复杂，维稳军事行动是我军当前重要的任务之一。维稳军事行动中，军械装备作为参与战斗的主要装备，军械装备维修任务量估算是科学筹划维修保障资源和维修保障方案的基础，越来越受到研究者的重视。

由于维稳军事行动较正规军事行动而言，具有事发突然、类型多样、地理环境条件不定等特点，给装备维修任务量估算带来了新的困难。

张芳玉将装备损坏划分为受击损坏、自然损坏和环境影响三种；綦海龙[1]运用历史资料总结方法，对装备维修任务模型进行了研究；汪文峰[2]基于一定统计分布，对武器装备备件维修任务预测方法进行了研究；刘玉文[3]等综合考虑火炮性能、环境、增援、损失等因素应用兰彻斯特方程对炮兵兵力对抗进行了研究。基于统计的任务量估算方法受到历史数据的制约，使其应用具有一定的限制。基于兰彻斯特方程的研究方法可以在一定程度上反应维修任务量的特点，陆凡[4]等从装备战损量预计出发运用兰彻斯特方程进行了研究，但由于其没有考虑维稳军事行动中武器装备不对称等特征，不能精确反应维稳军事行动特点。

本文考虑了作战双方武器装备水平不对等情况，突出了装备防护性等特点，建立了考虑装备的兰彻斯特方程，并给出了典型情况下的参数设置分析，由于本方法考虑了装备水平，使估算结果更具有针对性。最后给出了示例，表明本文研究的可操作性。

1 维稳军事行动战斗损伤影响因素分析

1.1 维稳军事行动主要任务

在维稳军事行动中，我军担负的任务主要包括以下几个方面：

（1）打击恐怖。对于拥有武装的恐怖分子，进行致命打击。破坏其恐怖能力，保障人民生命和财产安全。

（2）安全保卫。主要对重要地点、重点设施进行的安全保卫工作。

（3）恢复秩序。协助当地部门进行社会秩序、经济秩序重构。在紧急状态下进行局势控制。

在作战形式方面，主要包括炮兵防空兵精确打击、装甲兵突击攻防、工程兵战役工程保障、防化兵防化保障等形式。

在维稳军事行动中，对装备破坏最强的是打击恐怖过程中的装备损坏，下面主要针对打击恐怖作战过程进行军械装备损坏预计。

1.2 维稳军事行动作战对抗力量对比

维稳军事行动中，往往会有战斗行动。根据目前可能维稳方向的特点，对维稳军事行动对抗对象分析，可以为维稳军事行动军械装备损伤提供分析基础。维稳军事行动中，红方和蓝方的力量对比上，主要有以下几点：

我军（红方）对敌的力量优势主要体现在：

（1）在训练方面，进行维稳军事行动部队训练有素，蓝方往往训练不够正规；

（2）在装备方面，红方装备配置齐全，在准备充分的条件下，各种战斗装备很容易形成梯次，而蓝方由于受到其装备筹措限制，装备往往较单一，难以形成战斗体系；

（3）在体系作战方面，红方具有体系作战能力，协同能力强，而蓝方不具备体系作战能力，力量往往分散。

红方对敌的力量劣势主要体现在：

（1）红方在地形的熟悉方面可能不足。由于维稳军事行动往往需要红方赴其他地域进行军事行动，往往不是该部队熟悉的地域和气候环境，会为红方行动带来困难。

（2）红方作战准备可能不足。由于维稳军事行动发生突然，应急性强，而在极短的时间内，往往可能准备不足；而蓝方蓄谋时间较久，准备比较充分。

（3）红方对敌识别较蓝方困难。由于蓝方人员复杂，在维稳军事行动中，往往难以识别；而红方往往在着装等方面统一，容易识别，相对较易被蓝方进行识别。

1.3 打击恐怖作战任务影响因素分析

不同的作战任务对维修保障需求要求不同。由于打击恐怖作战过程强度不同，要求的维修保障也不相同。因此，需要对打击恐怖作战任务的影响因素加以分析。主要因素包括：

（1）作战规模。不同的作战规模维修保障需求也不相同。根据作战规模我军把作战分为战略、战役、战术三个级别。打击恐怖作战任务往往处于战术级别，极个别情况下可能形成战役级别。

（2）参战装备。战时红蓝双方参战装备数量和类型是配置维修保障力量的重要依据；双方参战武器装备的实力是装备受击损坏预测的主要参考指标之一，其中装备的战斗效能、使用强度是影响装备损坏的重要因素。

（3）作战部署。作战部署是战时装备保障部署主要依据，并且直接影响着维修保障力量的使用和能力的发挥。作战部队部署区域的面积以及与维修保障机构的距离既是衡量维修保障效率的重要指标，又是区分和部署维修保障力量的前提条件。作战区域内道路和地形状况等也是影响维修保障顺利实施的因素。

（4）作战行动。作战行动是构成作战任务的基本要素，是筹划维修保障行动的直接依据。通常，作战任务根据作战类型（进攻和防御）和样式划分作战阶段，各作战阶段战斗行动、作战目的、完成任务、激烈程度都不相同，因此，各个阶段对维修保障需求也不一样。所以，在筹划和安排维修保障行动时必须要与作战行动相协调。

（5）时间限制。作战时间主要包括战斗持续时间和各部（分）队作战行动实施的顺序时间，前者是维修保障单元开设和撤收时间的参考依据，是维修保障力量保障能力发挥的制约因素；后者是协调和组织保障力量在行动时间上与作战行动保持有序一致的重要依据。

2 基于兰彻斯特方程的军械装备战斗损伤预计

2.1 兰彻斯特基本方程

兰彻斯特方程又称兰彻斯特战斗理论或战斗动态理论，是应用数学方法研究敌对双方在战斗中的武器、兵力消灭过程的运筹学分支。1915年，工程师F.W.Lancaster在 《战斗中的飞机》一文中，首先提出用常微分方程组描述敌对双方兵力消灭过程，定性地说明了集中兵力的原理。

在远距离交战的时候，任一方实力与本身数量成正比，即兰彻斯特线性律。在近距离交战的时候，任一方实力与本身数量的平方成正比，即兰彻斯特平方律。兰彻斯特把战斗简化为两种基本情况：远距离交火和近距离集中火力杀伤。

（1）远距离交火情况

远距离交火时，一方损失率既和对方兵力成正比，也和己方兵力成正比，以微分方程表示即为：

其中，x和y分别为红军和蓝军的战斗单位数量，a和b分别为红军和蓝军的平均单位战斗力，因此双方实力相等的条件为：

（2）近距离交火情况

近距离交火时，一方损失率仅和对方战斗单位数量成正比，而和己方战斗单位数量无关，即：

双方实力相等的条件变为：

2.2 考虑装备的兰彻斯特方程研究

由于在维稳军事行动中，往往蓝方与红方武器装备不对等，对于不同武器对比来说，其对人员和对装备的损伤效果不尽相同，为了研究该情况，需要将不同武器装备对人员和装备的杀伤或毁伤分别加以考虑。为研究方便，做出如下假设：

（1）假设交火双方由独立的作战单元构成，每个作战单元由人员和武器组成，人员受伤或武器受损均导致该单元失去作战能力。不同的作战单元人员受伤和武器受损概率为固定值；

（2）交火双方距离较近；

（3）每种作战单元在一次战斗中受损的概率相同，为固定值；

（4）作战单元中，人员和武器同时受损伤，只记作武器受损。

列出该情况的兰彻斯特方程如下表示：

其中

x——蓝方作战单元数量

xi——蓝方第i种作战单元数量

ai——蓝方第i种作战单元杀伤系数

bi——蓝方第i种作战单元中人员受伤概率与武器受损概率比值

ci——蓝方受毁伤的第i种作战单元占总作战单元损伤数比例

vi——蓝方武器损伤数

y——红方作战单元数量

yj——表示红方第j种作战单元

aj——红方第j种作战单元杀伤系数

bj——红方第j种作战单元中人员受伤概率与武器受损概率比值

cj——红方第j种受毁伤作战单元占总作战单元损伤的比例

wj——红方第j种武器损伤数

上式中，第一个和第二个式子损伤总数与对方战斗力成正比，与兰彻斯特线性律相对应；第三个和第四个式子表示在总比例固定条件下，各种作战单元受损数量求解方法；第五个和第六个式子表示不同作战单元的人员和武器比例固定条件下，武器损伤数量情况。

通过求解上述方程，即可得到装备由于战斗损耗造成的维修任务量。

2.3 典型情况下参数设置分析

（1）a的设置

a对应于双方作战单元的战斗能力，与武器性能、人员训练素质、环境熟悉情况有关。一般来说，在维稳军事行动中，红方往往处于武器和人员训练素质均占优势的地位，由于红方往往为机动作战，在环境熟悉方面往往稍占劣势。

仅考虑武器本身的作战能力情况下[4]，可以参考表1所示。

表1 常见兵器火力指数

（2）b 的设置

b对应作战单元中人员和武器受损比例。比如人员使用轻武器组成的作战单元中，人员更容易受伤，武器受损概率相对较小；人员与坦克组成的作战单元中，人员不容易受伤，而武器受损概率相对较高。

（3）c的设置

c对应作战单元在其所有作战单元中防护能力，如果作战单元防护力量相对占优，则该作战单元在其受损单元所占比重较小。

3 示例分析

考虑红方作战单元数量为1 450个，蓝方作战单元数量为1 000个。其内部各种作战单元比例及参数如表2所示。

则有：

表2 参战作战单元数量及参数

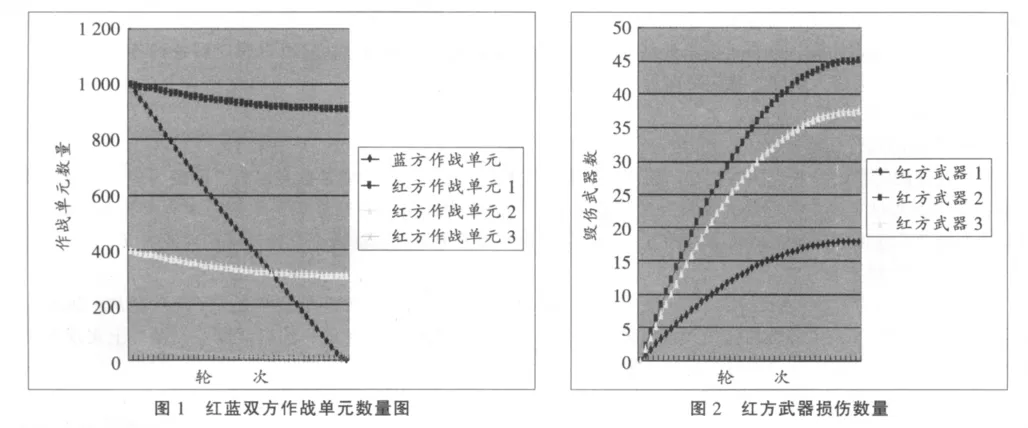
求解该式，可得蓝方全部被损伤后，红方作战单元I损伤91个，作战单元II损伤91个，作战单元III损伤46个。红蓝双方作战单元数量如图1所示。

上式中，求解得到红方武器I损伤数为19个，武器II损伤数为45个，武器III损伤数为38个。红方武器损伤数量如图2所示。

由此可知，红方损失武器数量总数为：

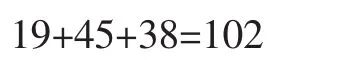
根据兰彻斯特方程，可以求解得到由于战损造成的维修任务。

[1]綦海龙，何志德.装备维修任务模型研究[J].航空计算技术，2006,36(2):124-126.

[2]汪文峰，宋黎.武器装备备件维修任务预测[J].装备环境工程，2009,6(5):42-44.

[3]刘玉文，侯明，薛晓中,等.一种改进的炮兵对抗兰彻斯特方程[J].弹道学报，2010,22(2):107-110.

[4]陆凡，郑怀州，刘志勤.兰彻斯特方程的装备战损量预计方法[J].火力与指挥控制，2008,33(5):144-147.