协调运行风险的发电机组优化调度研究

刘海峰 查 浩

1.海洋石油工程股份有限公司 天津 300452 2.中国电力科学研究院 北京 100192

0 引言

随着电力工业改革的不断深入和市场化进程的不断推进，满足一定运行风险水平的调度目标无疑应追求效益，然而运行中诸多不确定因素使得电力系统运行风险依然在不断增大，由此基于传统确定性方式进行机组优化调度，即不考虑机组故障事件发生的可能性，或者按指定预想事件进行调度，都难以定量化反映电力系统的运行风险水平，难免出现保守（如按N-1、N-2的调度）或冒进的现象［1-2］。在此背景下，考虑运行风险因素的发电优化调度研究与实践逐步成为热点问题［3-8］。电力系统运行风险评估［3］，目的在于综合度量不确定性因素的可能性大小和严重性程度，给出辅助运行调度人员制定调度计划的决策支持信息。在电力系统运行风险评估的思想框架下，围绕市场环境下电力系统运行安全、经济、可靠等相关层面的研究，已取得了诸多成果，如运行条件下元件寿命建模与预想事件状态的概率预测等基础研究［4］；电力系统在事故状态下严重程度的安全经济综合度量分析［5］；发电机组旋转备用的优化配置与效用评价［6］，需求侧可中断负荷的经济度量与风险决策［7］，等等。然而，对于短期的电力系统运行调度，统筹考虑预想事故发生概率及其后果的经济代价，有机协调运行安全性与经济性，制定协调运行风险的调度计划，则更能符合电网实际运行条件下的调度需要［8］。

因此，本文以传统发电优化调度理论为研究对象，建立了协调运行风险的机组优化调度模型，以机组故障事件发生概率为协调手段，以发电机组爬坡速率为牵制条件，有机协调了机组运行耗费、事故状态下输出功率再调整费用代价、以及负荷的中断赔付价值，以协调运行风险的方式将事故前后状态进行了牵制衔接，量化了机组的备用配置与责任划分。最后，通过与传统经济调度方式的对比分析，进一步揭示了模型本质。

1 数学模型表达

1.1 问题的提出

电力系统运行风险评估的基本思想可用下式表示：

式（1）中，Xt，f为电力系统的运行方式，NC为电力系统给定的预想事件个数；Pr（Ek）为第k个预想事件状态的发生概率；Sev（Ek｜Xt，f）为在当前运行方式Xt，f下，第k个预想事件的严重程度。 由此，Risk（Xt，f）值即为发电机组调度计划 在预想事件集合下的运行风险。

由式（1）可知，在电力系统发电优化调度中，机组取不同调度方式Xt，f便对应不同运行风险水平，有机考虑电力系统事故前后状态间的牵制与衔接，以均衡风险的方式给出最优发电调度计划，是本文研究的主要目的。

为有效度量发电调度计划的风险水平，在以下所构建的数学模型中，机组事故的严重性采用了货币化经济度量，即机组输出功率的费用函数、再调度费用函数采用二次表达，需求侧负荷中断量的赔付价值采用线性表达。因此，本文协调运行风险的发电优化调度模型是以期望运行耗费最小为目标，并满足电力系统事故前后各状态下的等式与不等式约束集。

1.2 费用函数表达

第i台发电机组的费用函数为：

式（2）中，PGi为机组i的有功功率输出，ai、bi和ci为给定的费用函数的常系数。

从事故前的正常运行调度方式出发，在发生机组停运的事件状态下，为了维持电力系统的供需平衡，非停运机组需进行再调度，或是进行紧急的中断部分负荷，由上述两项再校正措施所产生的费用代价可叙述如下。

机组输出功率再调整所引起的耗费：

需求侧紧急的中断负荷的赔付费用：

式（4）中，rk为电力系统在第k事故状态下的负荷中断量，a1为需求侧的负荷紧急中断的赔付价值系数。因此，C1（rk）描述了电力系统需求侧在第k事故状态下的损失价值，反映了负荷作为电力系统紧急备用资源的补偿代价。

1.3 目标函数表示

协调运行风险的发电优化调度模型以期望运行成本最小为目标，即：

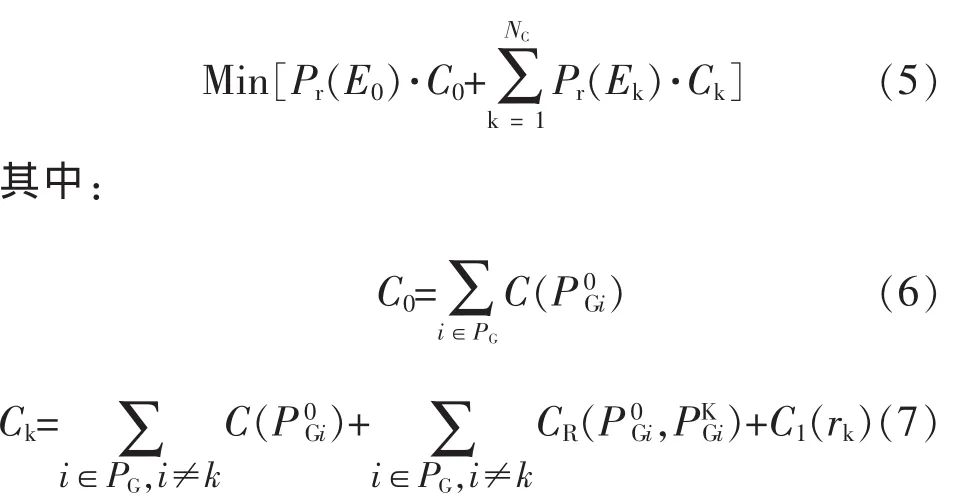
式（5）是本文模型的目标函数表达式，即机组事故前和NC个机组预想故障事件状态下的期望运行总费用达到最小。其中Pr（E0）和Pr（Ek）分别对应发电机组在事故前状态和第k个事故状态的发生概率。C0和Ck分别对应着发电机组在事故前状态和第k个事故状态下的运行耗费。

式（6）对应着发电机组在事故前状态的运行总耗费，其中PG表示发电机组集合。

式（7）对应着发电机组在第k个事故发生状态下的运行总费用。

因此，式（5）～（7）构成了本文模型的目标函数，以风险均衡方式有机关联了发电机组停运事故前后状态之间的费用牵制。

1.4 约束条件表达

本文模型的约束集合包括了发电机组事故前后各状态下的功率平衡约束和机组输出功率限值约束，以及事故前后状态间所对应的耦合牵制约束，即发电机组旋转备用的响应速率约束，具体描述如下。

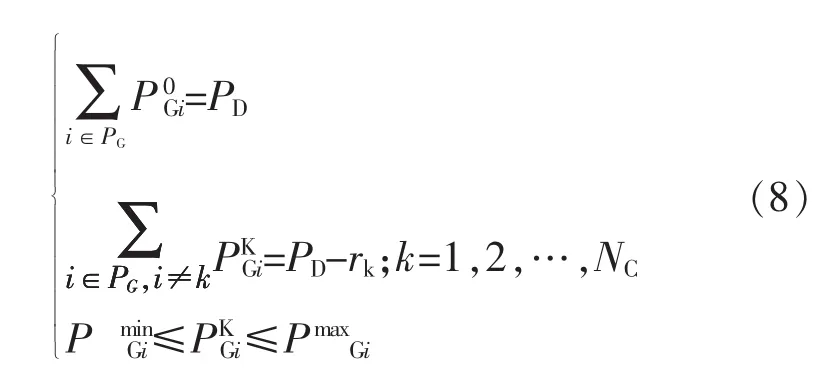
发电机组事故前后各状态下的功率平衡等式和不等式约束：式中，PD为系统应满足的负荷需求，PminGi、PmaxGi为第i台机组输出功率允许的下限和上限。

式（8）给出了发电机组事故前状态和NC个预想事故状态下的功率平衡等式约束，以及发电机组事故前后各状态下的输出功率限值约束。

发电机组事故前正常状态与第k个事故状态之间所对应的输出功率速率调整耦合牵制约束：

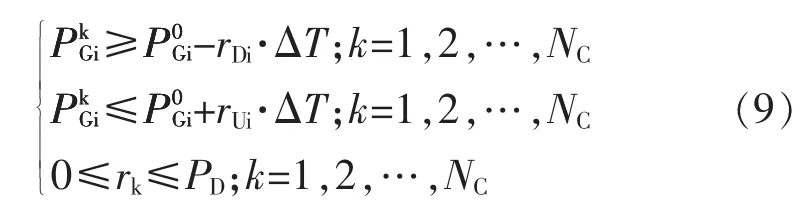
式（9）中，rUi和rDi分别对应第i台发电机组有功功率输出的最大上下允许调整速率，ΔT对应于事故状态下所容许的发电机组紧急再调度调整延续时间。因此，式（9）给出了电力系统在事故后发电机组旋转备用量的有效调整范围。

因此，式（2）～（9）构成了本文所提出的协调运行风险的发电优化调度模型。

2 模型分析及求解

2.1 模型分析

上节所给出的协调运行风险的发电优化调度模型，综合分析可知该模型包含如下情况：

1）若不考虑发电机组停运事件影响，模型变为以发电机组运行费用最小为目标，只满足正常状态下的功率平衡约束及相关不等式约束，这样，该调度方式即对应为传统经济调度。

2）若以确定性方式考虑发电机组停运事故影响，即忽略其发生概率，则模型变为以发电机组运行费用最小为目标，满足事故前后状态下的功率平衡及旋转备用调整牵制。因此，该方式给出的是在预想事件集下的确定性调度计划。

3）若同时考虑发电机组停运事故的发生概率与经济代价，则该模型即以发电机组期望运行费用最小为目标，满足事故前后状态对应的等式与不等式约束集合。这样，该方式关联了发电机组故障事件的发生概率及其经济后果，给出了均衡协调的调度计划。

通过上述分析可知，本文模型是对传统发电优化调度理论的继承和发展。

2.2 模型求解

针对本文中所提出的问题，其中选取可信的机组预想事故，有效预测机组事故状态的发生概率，以及对调度模型进行解算，是该问题求解的几个关键环节。为了突出本文理论研究，分析模型的机理，现将解算流程叙述如下。

为简化问题计算规模，本文依照N-1规则对发电机组预想事故集进行了指定，但事故状态数量仍可实际依照需要进行增减修订，这并不影响本文解决问题有效性的实质。

对于运行条件下的机组事故状态概率的求取，可采用文［8］中的马尔可夫链计算方法，在预测得到相关发电机组未来运行状态概率的基础上，各相关事故状态概率值可通过发电机组状态概率连乘获取。此过程本文不再给出，假定机组事故状态发生概率为已知。

因此，在得到预想事故集合及其发生概率后，本文采用原对偶内点法对本文模型进行了解算，算法细节在此不再详述。

3 算例分析与验证

以6机组系统为例，对本文模型进行论证分析。表1给出发电机组相关特性数据，其中Pr（Ek）为第k台机组发生事故的状态概率，系统需要满足的负荷量为600MW，紧急中断负荷赔付价值系数为1000$/MW。发电机组在预想事故后所能容许的紧急再调度延续时间取值为ΔT=5 min。

结合文中2.1节所叙述的3种调度方式，为有效揭示本文模型机理，以下对情况1～3这3种方式的调度计算结果进行详细分析。

表2中给出了方式1调度计算结果，发电机组PG1～PG6的有功功率输出如表中所示，系统运行费用Cost数值为40118$。由于方式1调度未考虑机组停运的影响，在机组事故状态下将面临高额的负荷中断赔付，因此调度计划是有风险的，存在冒进行为，然而按经济理论，事故前该调度方式的运行费用为最小。

表1 机组相关特性参数

表2 方式1调度结果

表3 方式2调度结果

表3中给出了方式2调度的计算结果，机组有功功率调度值如表中所示，系统在事故前状态的运行费用Cost数值为40438$。方式2调度考虑了机组停运事件的影响，但以确定性方式来处理，未计入机组停运事件状态的发生概率，因而调度运行费用最高，发电计划有所保守。

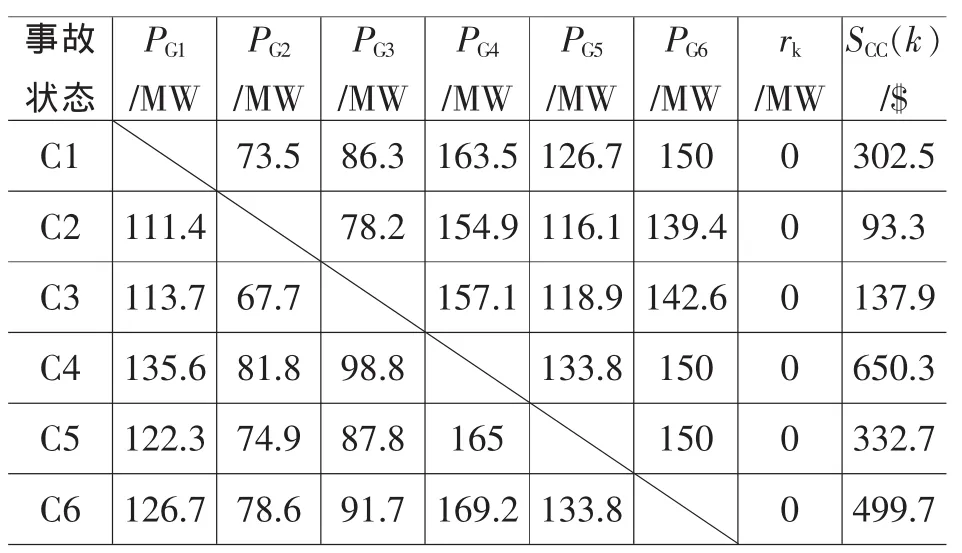
表4 方式2事故状态下的再调度结果

表4中给出了从方式2调度出发，各个事故状态下的机组优化调度策略。C1～C6对应各台发电机组的停运事故状态。机组在事故状态下的有功功率调度值如PG1～PG6所示。各事故状态下的负荷中断量由rk所示。

分析表4可知，方式2调度未出现预想扰动事件集合内的负荷中断情形。安全校正耗费（Security corrective cost，SCC）为第k台机组发生停运所引起的经济代价，SCC（k）即事故k状态下的旋转备用调整耗费和负荷中断赔付费用之和。

机组预留旋转备用是为抵御随机不确定性事件而配置，方式2事故再调度给出了旋转备用的实际效用与事故状态间的映射关系。通过对表4中的事故再调度结果分析可知，事故状态下各机组输出功率值对应机组经济再调整的校正策略，SCC（k）数值表征了各机组停运事件所引起的经济代价，因此方式2事故再调度策略量化了机组事故大小的责任划分，蕴含了备用共享、责任明晰的配置理念。但是，由于方式2未考虑发电机组停运事件的发生概率，无法给出调度决策的运行风险。以下着重分析方式3调度计算结果。

表5 方式3调度结果

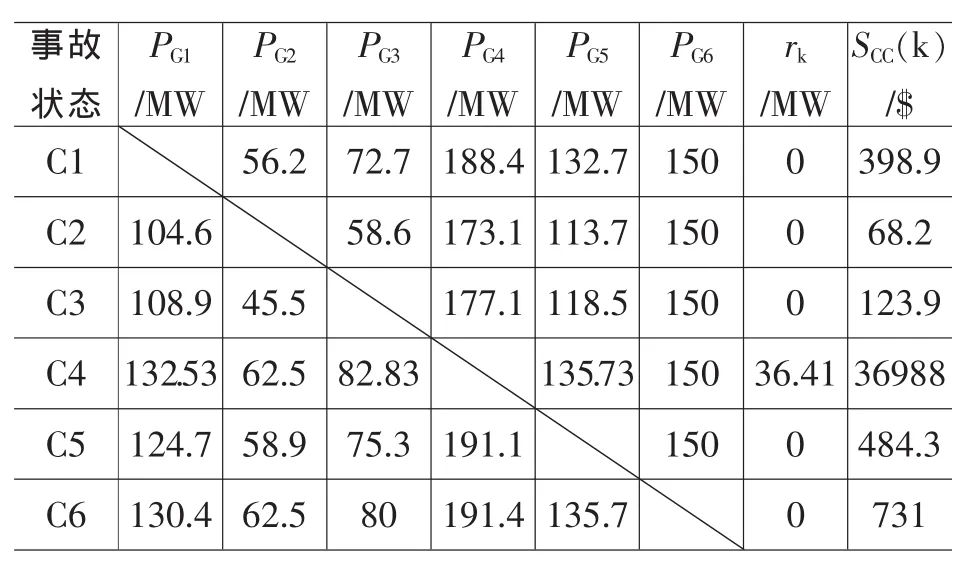
表6 方式3事故状态下的再调度结果

表5中给出了方式3调度的计算结果，机组输出功率调度值如表中所示，系统事故前状态的运行费用Cost数值为40187$。由于方式3同时考虑了机组停运事件的可能性概率和严重性程度，以均衡运行风险的方式协调了机组事故前后状态之间的经济牵制，因此运行费用介于方式1和方式2之间，既不保守，也不冒进，是综合折中的发电机组优化调度方案。

表6给出了方式3事故后的再调度结果，对应各事故状态下的机组输出功率再调整结果和负荷中断量值。从表中可见，第4台发电机组发生停运后的C4事故状态将会出现负荷中断情形，表明方式3调度对应一定的失负荷风险，数值大小即为事故状态C4的发生概率0.005。

4 结论

本文所提出的协调运行风险的发电机组优化调度模型，避免了以往沿用传统可靠性思想对调度模型进行评估的方式，而是以概率手段对调度方式及其对应后果进行了有机协调。通过对模型所涵盖的3种不同方式进行分析，进一步阐述了协调运行风险的折中调度决策理念，实现了协调运行风险的发电机组优化调度，量化了旋转备用配置与机组事故的责任划分，符合电力市场环境的经济机制。

［1］Condren J， Gedra T W， Damrongkulkamjorn P.Optimal power flow with expected security costs ［J］.IEEE Trans.on Power Systems， 2006， 21（02）： 541-547.

［2］Aganagic M， Awobamise B.Economic dispatch with generation contingency constraints ［J］.IEEE Trans on Power Systems， 1997， 12（03）： 1229-1236.

［3］冯永青，张伯明，吴文传 等.基于可信性理论的电力系统运行风险评估：（一）运行风险的提出与发展［J］.电力系统自动化， 2006， 30（01）：17-23.

［4］刘海涛，程林，孙元章等.基于实时运行条件的元件停运因素分析与停运率建模 ［J］.电力系统自动化，2007，31（07）：6-11.

［5］Ni Ming， McCalley J D， Vittal V.Online risk-based security assessment ［J］.IEEE Trans.on Power Systems，2003， 18（01）： 258-265.

［6］齐先军，丁明.发电系统中旋转备用方案的风险分析与效用决策［J］.电力系统自动化， 2008， 32（03）：9-13.

［7］赖业宁，薛禹圣，江德星 等.备用容量服务市场的风险决策［J］.电力系统自动化，2006， 30（16）：1-5.

［8］查浩，韩学山，杨朋朋.电网运行状态下的概率优化调度［J］.中国电机工程学报， 2008， 28（28）：54-60.