减振型板式轨道的模态分析
2011-05-04刘亚航徐金辉杨荣山
代 丰,刘亚航,徐金辉,杨荣山
(西南交通大学 高速铁路线路工程教育部重点实验室,成都 610031)
随着我国铁路客运专线的修建和城市轨道交通的发展,振动噪声问题也引起了社会各界的广泛关注,因而相继研究开发了各种减振降噪型轨道结构。减振型板式轨道因其减振效果好,在我国和日本使用广泛。我国京沪高铁北京—上海段、武广客运专线瓦屋特大桥段、遂渝线无砟轨道综合试验段等均采用此种轨道结构形式,并取得了良好的经济效益和社会效益。本文将模态分析方法应用于减振型板式轨道的结构振动研究中,根据模态分析理论,建立钢轨—扣件—轨道板—自密实混凝土—减振垫层相互作用的有限元计算模型,对组合结构参数条件下的减振型板式轨道进行了计算分析,为优化轨道结构的减振设计进行了探索。
1 减振型板式轨道的结构设计
减振型板式轨道由钢轨、扣件、预制混凝土轨道板、轨道板下橡胶垫层、乳化沥青水泥砂浆调整层、混凝土凸形挡台和混凝土底座等组成。其主要结构特征为:①为提高弹性和降低成本,并且防止板下胶垫被挤出,采用带沟槽式板下胶垫;②为减轻由自身变形所产生的约束及改善应力分配,采用中空方式。
参考成灌线离堆公园支线(D1K47+563—D1K51+509)隧道地段单元板式无砟轨道结构形式,如图1所示。该结构在混凝土底座上表面设置20 mm厚的减振垫层,两边采用高、低刚度减振橡胶垫层配合布置,中部采用聚乙烯闭孔泡沫板,如图2所示。在底座板上设置两个凹槽,以约束轨道板的纵向和横向位移。

图1 减振型板式轨道

图2 减振垫层平面
2 计算模型
2.1 计算模型参数
相比普通板式轨道,减振型板式轨道多了一层减振层,其余轨道结构与普通板式轨道相同。钢轨采用60 kg/m钢轨,弹性模量为2.06×105MPa。轨道板的长度为 5.35 m,宽 2.50 m,高 0.19 m,弹性模量为3.65×104MPa。高刚度减振层的长度为1.40 m,宽0.90 m,厚0.02 m,弹性模量为1.85 MPa。低刚度减振层的宽度和厚度同于高刚度减振层,长度为1.275 m,弹性模量为1.1 MPa。自密实混凝土层的长度、宽度、高度分别为5.35 m,2.70 m,0.10 m,弹性模量为3.25×104MPa。底座板上凹槽的长度、宽度、高度分别为0.40 m,0.60 m,0.142 m,凹槽四周的橡胶弹性模量为2.0 MPa。
2.2 计算模型的建立
本文研究的是减振型板式轨道,由于混凝土底座设有凹槽,轨道结构并非等厚层,为准确地反映单元板式减振轨道的结构特征和受力特性,采用有限元理论,运用ANSYS有限元软件建立钢轨—扣件—轨道板—自密实混凝土—减振垫层相互作用的有限元计算模型,如图3所示。
在有限元计算模型中,钢轨采用Beam188单元来模拟,通过自定义钢轨截面为梁截面,以更为真实地模拟钢轨截面形状;轨道板、自密实混凝土层采用Solid45实体单元模拟;扣件的垂向和横向支承刚度用线性弹簧单元Combin14模拟,由于扣件纵向支承刚度一般为非线性变化,故扣件纵向支承刚度用非线性弹簧单元Combin39模拟;高刚度减振层和低刚度减振层也采用线性弹簧单元Combin14模拟,提供垂向的弹性约束;凹槽提供纵向和横向的弹性约束,其四周用Combin14单元模拟。

图3 减振型板式轨道有限元计算模型
针对扣件垂向刚度和支承间距的不同,考虑9种工况,如表1所示。

表1 工况设置
3 模态分析
3.1 模态分析原理
对于轨道结构,模态分析法就是利用模态振型矩阵的线性组合形式进行模态坐标变换,将其振动微分方程中的物理坐标变换为模态坐标,使方程解耦,成为一组以模态坐标和模态参数描述的独立方程,可以像单自由度系统那样求出其模态响应,进而得到系统在物理坐标下的响应。
轨道结构的强迫振动方程为

式中,M,C,K为轨道结构的质量矩阵、阻尼矩阵、刚度矩阵。
阻尼矩阵C为经典阻尼,即满足 CM-1K=KM-1C,那么阻尼矩阵C可通过实模态变换x=Φη,利用模态矩阵正交性使方程解耦。从而得到其强迫振动响应。其中,Φ =[φ1,φ2,…,φn]n-n为模态振型矩阵,η为模态坐标。
3.2 模态计算与结果分析
3.2.1 固有频率
采用Block Lanczos法,对减振型板式轨道结构进行计算。理论分析和实际经验表明,轨道结构的低阶模态更具研究价值,通常前几阶或几十阶模态已可获得足够精确的结果。本文扩展模态设为10阶,得到9种工况下,减振型板式轨道的前十阶固有频率,如表2所示,固有频率的变化趋势,如图4所示。
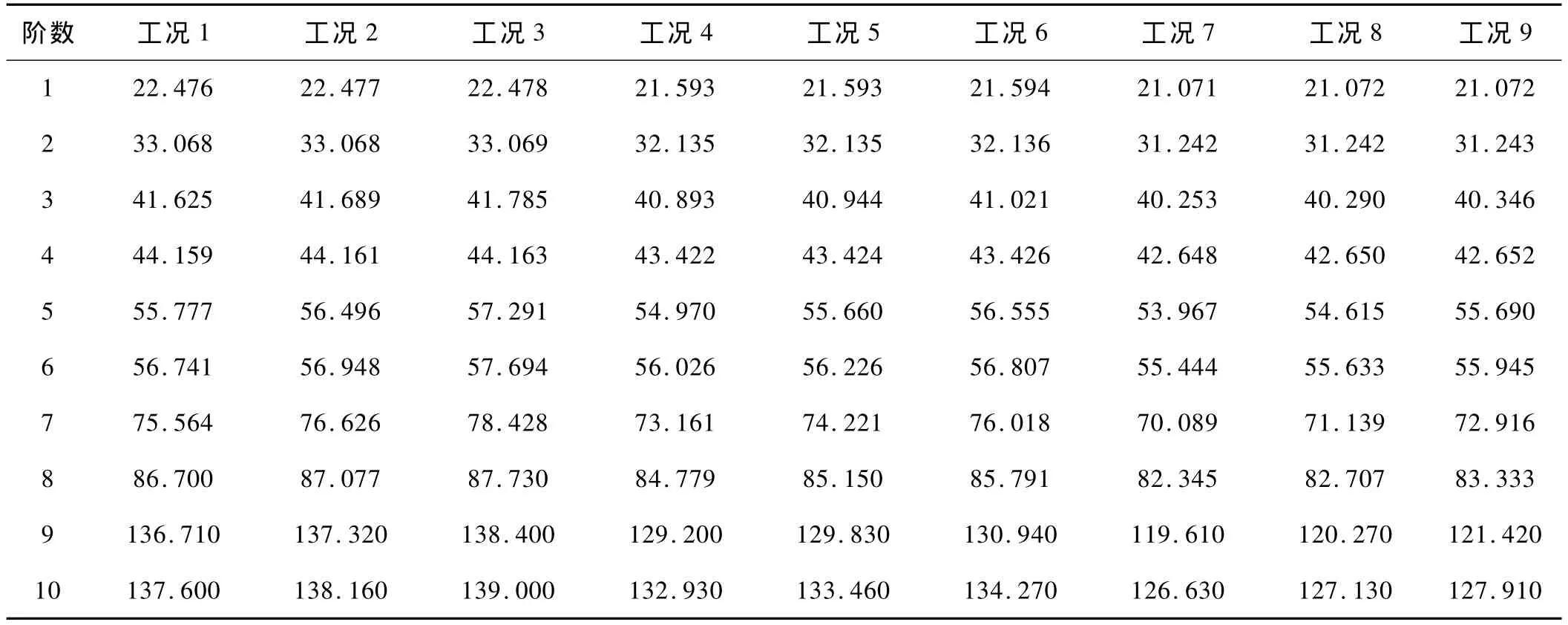
表2 9种工况下轨道结构的前十阶频率 Hz
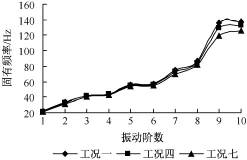
图4 系统固有频率随支承间距的变化趋势
由表2,图4可知,减振板式无砟轨道结构的固有频率随振动阶数的增加而逐步增加。减振板式轨道结构前8阶的固有频率增加较为平缓,没有出现数量级上的跳跃。在减振板式轨道结构的前8阶固有频率中,相邻两阶固有频率之间最大相差20.734 Hz,最小的相差0.252 Hz。减振板式轨道结构的第8阶和第9阶固有频率在数量级上有跳跃,这样使得更高阶的振动难于激发。扣件刚度和支承间距的变化对系统的低阶固有频率几乎没有影响,因此在研究轨道的减振性能时,可不考虑扣件刚度和支承间距的影响。
为研究轨道结构的振动特性,可从改变系统的参振质量入手。轨道板厚度的变化导致系统参振质量的变化。几种不同轨道板厚度的系统固有频率变化情况,如图5所示。
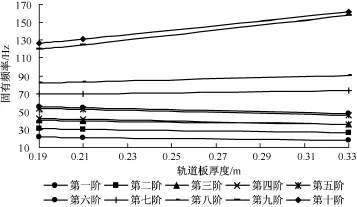
图5 系统固有频率随轨道板厚度的变化趋势
由图5可知,随着轨道板厚度的增大,系统前6阶频率逐渐减小,而后几阶频率却相应增大。增加轨道板的厚度可以增加其参振质量,降低系统的固有频率,同时也增加了轨道板的抗弯刚度,减少轨道板本身及整个轨道结构的变形,从而减小作用于钢轨的附加应力,提高车辆运行的安全性和平顺性。
3.2.2 振型
振型为系统的固有特性,是对应固有频率系统自身振动的形态。每一阶固有频率对应于一种振型。减振板式轨道结构的前8阶振型如图6~图13所示。
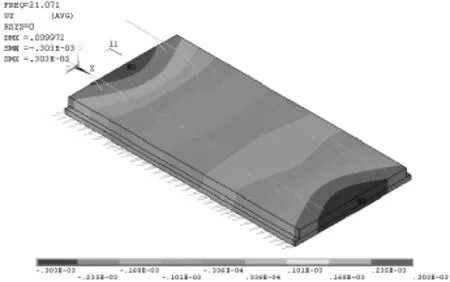
图6 减振板式轨道结构第一阶振型(单位:m)

图7 减振板式轨道结构第二阶振型(单位:m)
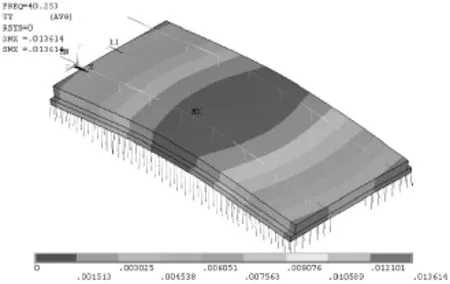
图8 减振板式轨道结构第三阶振型(单位:m)
由图6~图13可知,①减振板式轨道结构的模态振型主要有弯曲和扭转两种形式,而这两种模态振型是通过结构的横向、垂向和纵向振动体现出来的。②在一阶振型中,轨道结构主要发生纵向振动,振幅峰值出现在纵向板端。③二阶振型主要发生横向振动,基本没有垂向振动,位移峰值均布于横向板端,且代数值相等。④三阶振型主要发生垂向振动,基本没有纵向振动,垂向位移的最大值出现在轨道的横向对称面上,沿两边均匀递减。⑤在四阶振型中,由横向、纵向与垂向三个方向振动的叠加,以轨道中性面和纵向对称面的交线为轴发生扭转,位移的最大值与最小值交替出现在轨道板的四个角点,且代数值相等。⑥五阶振型由于垂向振动和纵向振动的叠加,轨道板沿纵向弯曲。⑦在高阶振动中,轨道板自身的变形越来越大,高阶振型的固有频率受轨道板抗弯、抗扭刚度的影响更大,造成轨道结构的高阶振动愈难激发。
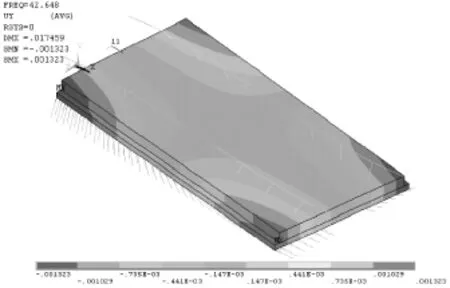
图9 减振板式轨道结构第四阶振型(单位:m)
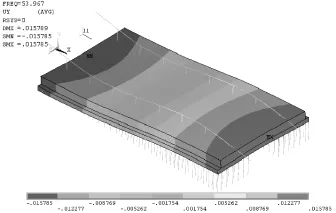
图10 减振板式轨道结构第五阶振型(单位:m)

图11 减振板式轨道结构第六阶振型(单位:m)
4 结论
1)对于减振型板式轨道结构,支承间距和扣件垂向刚度对系统固有频率影响很小,增加轨道板厚度可有效地减小系统的固有频率。

图12 减振板式轨道结构第七阶振型(单位:m)
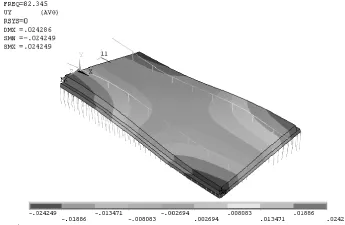
图13 减振板式轨道结构第八阶振型(单位:m)
2)轨道结构的前三阶振动主要体现在纵向、横向和垂向振动;在四阶及更高阶振型中,轨道结构的振动主要体现在纵向、横向、垂向上的叠加以及扭转。这是由于减振板式轨道结构减振层的作用,削弱了抵抗垂向变形的能力,而结构抵抗纵向和横向的能力也较弱,减振板式轨道结构较易激发自振。
[1]中川宪治.工程振动学[M].上海:上海科学技术出版社,1981.
[2]龚曙光,谢桂兰,黄云清.ANSYS参数化编程与命令手册[M].北京:机械工业出版社,2009.
[3]李成辉.轨道[M].成都:西南交通大学出版社,2004.
[4]盖晓野,张丽平,赵坪锐.现浇道床板弹性模量变化对结构的影响分析[J].铁道建筑,2010(10):100-102.
[5]耿传智,吴觉波.模态分析在轨道振动特性研究中的应用[J].上海:上海铁道学院学报,1995(1):13-23.
[6]杨祖旺.轨道交通钢轨的振动特性及其动力吸振技术研究[D].哈尔滨:哈尔滨工业大学,2006.
