GRNN在边坡稳定预测分析中的应用

狄圣杰,李晓敏,魏 樯

(1.河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098;2.郑州科技学院土木与建筑工程系,河南 郑州 450000;3.中国水电顾问集团昆明勘测设计研究院,云南 昆明 650051)

岩土体具有复杂的结构和机理,破坏过程是渐变性的,是变形积累到一定程度表现出宏观滑移的一个非线性复杂过程,如边坡滑动蠕动或挡土墙后楔形岩土体的开裂滑动,岩土体物理力学特征和地质环境因素对其都有影响,这些影响因素有的是确定的,有的是随机的,它们对不同类型边坡稳定性的影响权重也是不同的,之间又有复杂的非线性关系[1-2]。运用现代智能方法如人工神经网络已成为预测边坡稳定性的一种较有效的手段,其特点是智能性、综合性、集成性和非线性。

常用的BPNN(误差反向传播神经网络)及其改进方法无法自动调整结构组成,性能优良的BPNN需要优化网络结构,优化权值、阈值等参数,选择合理的计算方法和学习参数。这些都用到了相关的优化算法,例如用遗传或粒子群算法对未知参数寻优,必要时还要扩展网络结构以减小系统误差,同时收敛速度较慢,这会限制它在实际中的应用和推广。广义回归神经网络(GRNN)结构设计简单,收敛速度快,所需训练样本少,对被建模对象的先验知识要求不多,具有全局逼近性和最佳逼近性质,鲁棒性及非线性处理能力强,能根据样本数据反映其中隐含的映射关系,且不存在局部最小问题,目前已在工程中得到了应用[3-4]。

GRNN唯一需要调整的参数是光滑因子,它的选择对于网络性能优劣有较大影响,光滑因子越小,拟合程度越好,但过小会导致过拟合。文献[5-7]选取了光滑因子试算范围内的最小值,因为最小值不等于最优值,故直接应用某范围内的最小值是不准确的,会导致网络泛化能力差。笔者应用遍历样本的交叉验证方法,可以合理地选择光滑因子值,改善网络泛化能力,提高预测精度。

1 GRNN基本理论

GRNN是一种建立在非参数估计基础上的非线性回归的径向基神经网络,不需要事先确定方程形式,而以概率密度函数代替固有的方程形式,直接计算出因变量对自变量的回归值。其优势在于不需要重复训练,网络建成的同时训练即完成,网络的训练过程实际上就是确定光滑因子的过程,并且在网络数据稀少时效果也较好,能够收敛于样本量聚类较多的优化回归面。网络输入层只传递输入向量到径向基层,隐含层中神经元个数由所描述的问题而定,通常传递函数采用高斯函数radbas:

式中:aj为经过高斯函数传递后的网络输出;nprod为规范化点积权函数,是线性输出层的权值函数;‖dist‖为欧氏距离函数,即该层权值函数;bj为第j个隐含层与光滑因子有关的阈值;σj为光滑因子(spread),它决定第 j个隐含层位置处基函数的形状,σj越大基函数越平滑。

GRNN的每次训练都会自动检查输出误差,所产生的最大误差对应的输入向量会作为权值产生一个新的隐含层神经元,然后,新网络会循环检查误差直至神经元数量达到最大或达到一定精度为止。

初始化即训练样本的学习过程,学习样本确定了,则相应的网络结构和各神经元之间的连接权值也随之自动确定,网络训练过程实际上是确定光滑因子的过程。较BPNN而言,GRNN的人为调节参数仅为1个,网络学习全部依赖于数据样本,这就决定了网络得以最大限度地避免人为主观假定对计算结果的影响。同时GRNN解决了BPNN训练时间长且确定隐含层数目难的问题,能稳定地描述系统的特征。

2 光滑因子的影响分析与选取方法

2.1 光滑因子的影响

一般情况下,训练能力差时网络的预测能力也差,并且在一定程度上随着训练能力的提高预测能力也会提高,但这种趋势有一个极限,达到此极限后,随着训练能力的提高,预测能力反而下降,即出现所谓过适性,也称为过拟合,此时网络学习了过多的样本细节而不能反映样本内在的规律。泛化能力差会造成不适性,过适性和不适性的网络都属于不成熟网络,仿真效果较差[8]。

创建输入输出样本和广义回归神经网络,输入样本在[-1,1]区间内均匀地取21个点,21个数据点坐标如图1所示。当光滑因子取较小值0.02时,用步长0.01来检验拟合效果,观察所选光滑因子是否能够体现出所给样本内在的规律性。从图1(a)中可以看出,网络记住了训练样本细节,甚至个别噪声,曲线较陡,在原始样本点处形成平台,附近的数值向其值靠拢。当光滑因子取较大值0.2时,从图1(b)可以看出,网络进行函数逼近时拟合效果较差,出现了不适性。总体来说,光滑因子值越小,拟合越好,曲线越不光滑,但光滑因子太小时不能学习到真正的规律性,这样就对测试样本或仿真样本不敏感,即表现出过适性,以此网络来推广仿真势必会造成较大的误差。

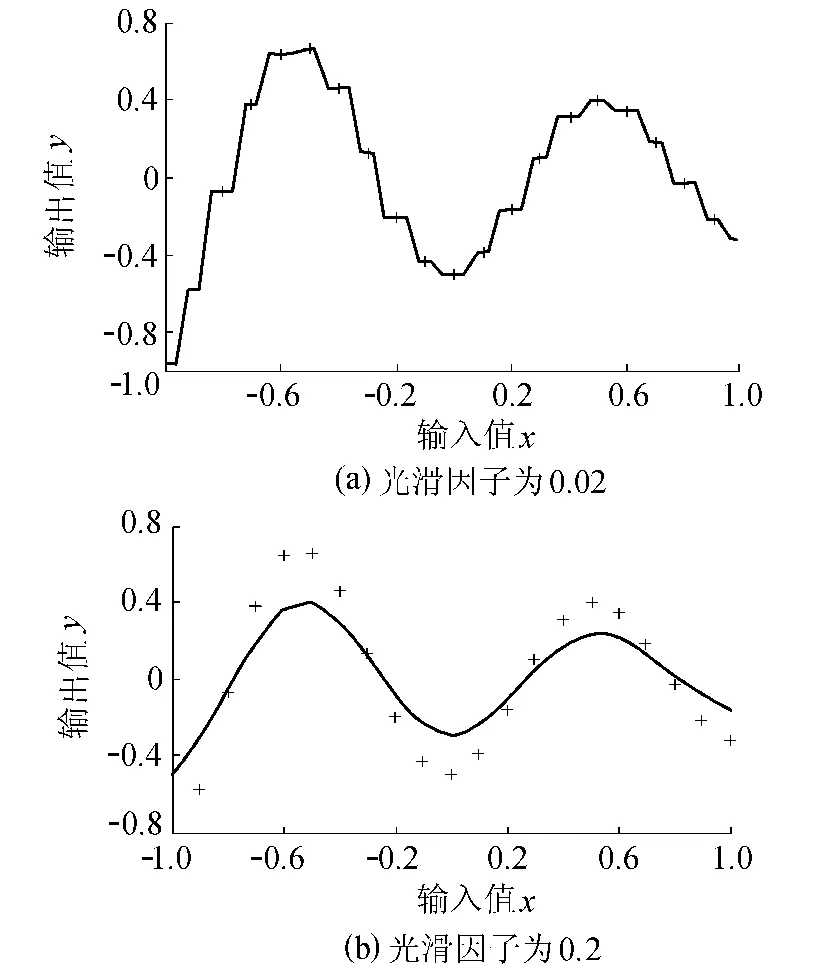
图1 训练样本的过适性与不适性

2.2 光滑因子的选取

采用LOO交叉验证方法评估模型的预测能力,即在一定范围内以某一步长递增变化,在学习样本中以1个样本作为估计样本,剩余的样本采用构造的GRNN对估计样本仿真,对所有样本都遍历1次,得到预测值与样本值之间的误差序列,以序列均方误差值作为网络的评价指标,将最小误差对应的光滑因子作为最终所选值。光滑因子的确定过程符合整体偏差最小原则[9-11]。

式中:E为预测值与样本期望值的方差;Xi为第i个样本对应的输入值;Yi′(Xi)为第 i个样本的预测值;Yi为样本期望值;n为样本个数。

训练样本中选择某列数组作为估计样本,用剩余的样本构造学习样本,依次对所有样本遍历1次,具体表达如式(3)、式(4)所示:

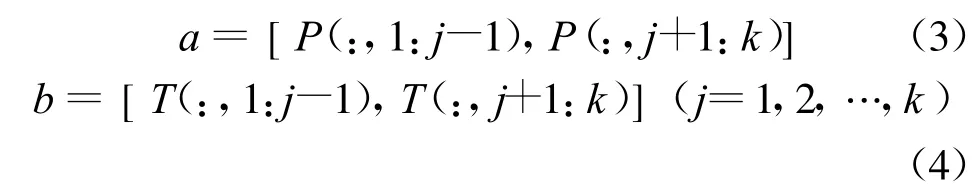
式中:a,b分别为训练样本和期望样本;P为输入样本;T为输出样本;k为输入或输出数组的列数,可以控制光滑因子的精度。

应用上面所示的样本可以求得光滑因子迭代值,其中用训练样本a代替输入样本P,用期望样本b代替输出样本T,即依次取出j列作为测试样本,剩余所有列作为训练样本,仿真后与理论值或实测值比较。

在确定平滑因子的过程中,初始值选取太小,式(4)可能出现除数为零的情况,文献[3]给出了初始值的计算公式:

式中:σmin为光滑因子选取区间的初始值;Dmin为学习样本中各输入样本之间Euclid距离的最小值;ε为计算机能够表达的最小正数。

以步长为0.01检验网络的拟合情况,选用误差最小时对应的光滑因子(此时光滑因子为0.058),网络仿真与训练样本如图2所示,拟合效果较好。对于一般问题,按照上述方法确定的平滑参数即可满足要求,也可建立优化问题模型,并应用传统和新型优化方法解决该问题。

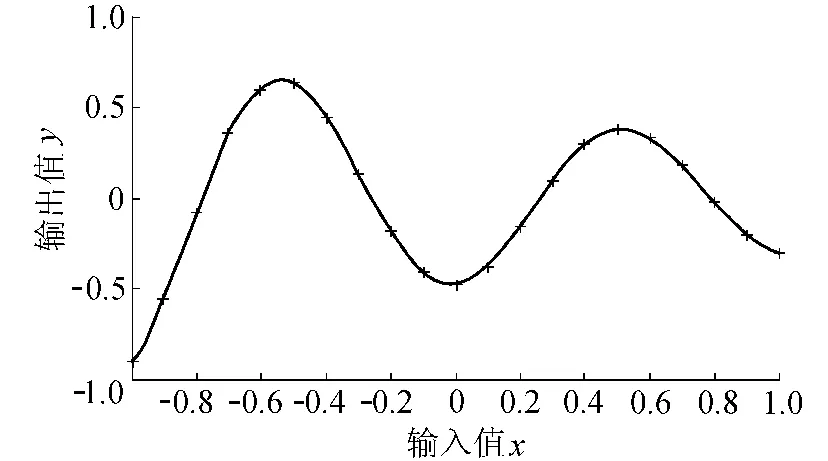
图2 GRNN的逼真函数

3 应用实例及模型对比分析

为了得到比较好的预测效果,一般在网络训练前应对原始数据作预处理,包括剔除离散性较大的值,对数量级差别较大的数据作归一化或标准化处理,对输出向量作反处理变换至原单位(如不存在相对于其他输入样本特别大或特别小的样本矢量可不进行归一化)。归一化时对输入输出向量正则化处理,使其落入[-1,1]区间,或归一到其单位方差和零均值,计算完毕后需要对结果数据还原。简单归一化和反归一化方法处理见式(6)、式(7):

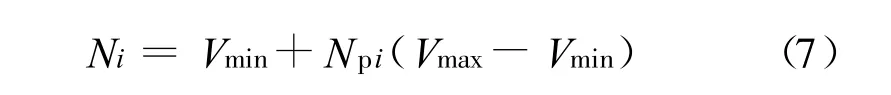
式中:Mi为原始输入值;M′i为归一化后的网络输入值;N p i为在[0,1]区间的预测值;Ni为预测值的还原值;Vmin和Vmax分别为样本最小值和最大值。

算例 对82个实际工程边坡的极限平衡分析统计资料和边坡对应状态(表1)分析可以发现,由于分析信息的模糊性、不确定性,即使计算安全系数大于1.6,也有部分边坡最终发生失稳破坏。训练样本为密度 ρ、黏聚力c、摩擦角 φ、残余摩擦角 ψ及坡高Η,目标样本为安全系数和稳定状态。边坡稳定状态为0代表破坏,1代表稳定,利用GRNN具备的聚类分类原理可以初步评判边坡稳定状态。

表1 82个实际工程边坡的统计资料与边坡稳定状态

样本1～79作为训练样本,样本80～82作为测试样本。对样本归一化处理后GRNN迭代搜索出的平滑因子值为0.143,安全系数预测结果为1.2000,1.5195,1.2000;BPNN的预测结果为1.2063,1.5304,1.1584,模型的预测结果如表2所示。从表2可以看出,即使存在安全系数大于1.6而产生破坏的干扰样本(表1中样本45),但总体预测情况仍然是良好的,GRNN预测的安全系数误差很小,最大为0.03%,而BPNN预测的安全系数最大误差不超过3.5%。另外GRNN在计算过程中的快捷更显示了其优越性。

?

4 结 语

a.讨论了GRNN网络中光滑因子的影响,光滑因子选取不当会造成网络的泛化能力差。根据光滑因子的初值,提出使用LOO交叉验证方法将得到的序列均方误差值作为网络的评价指标,最小误差对应的光滑因子即为所选值,并验证了该方法的合理性。

b.搜集了82个圆弧滑动边坡稳定性样本,由于分析信息的模糊性、不确定性,即使计算安全系数大于1.6也有部分边坡最终发生失稳破坏。结合本文提出的光滑因子选取方法,应用GRNN模型进行预测分析,吻合效果较好,反演精度较高,网络操作简捷,易为工程人员接受,可在工程实际中应用。

c.由于GRNN具有较强的函数拟合和逼近能力,其对样本依赖性强的特点使得选取具有代表性的训练样本数据非常重要,如果预测误差过大可能是数据的问题,关于如何减小训练样本数据中的误差或噪声对预测精度的影响需做进一步研究。

[1]狄圣杰,徐卫亚.黏性土求主动土压力的库尔曼法及应用[J].岩土工程学报,2010,32(6):970-974.

[2]张玉,张方方.变水位多工况下大型渠道土质边坡的稳定分析[J].水利水电科技进展,2010,30(1):56-60.

[3]TOMANDL D,SCHOBER A.A modified general regression neural network with new efficient training algorithms as a robust‘black box' tool for data analysis[J].Neural Networks,2001,14(4):1023-1034.

[4]周昊,郑立刚,樊建人,等.广义回归神经网络在煤灰熔点预测中的应用[J].浙江大学学报:工学版,2004,38(11):1470-1482.

[5]兰海涛,李谦,韩春雨.基于广义回归神经网络的边坡稳定性评价[J].岩土力学,2009,30(11):3460-3463.

[6]周建萍,闫澍旺.广义回归神经网络预测加筋土支挡结构高度[J].岩土力学,2002,23(4):486-490.

[7]冯志鹏,宋希庚,薛冬新,等.基于广义回归神经网络的时间序列预测研究[J].振动、测试与诊断,2003,23(2):105-144.

[8]DI Sheng-jie,XU Wei-ya,WEI Qing.The selection of spread and the application in engineering of GRNN[C]//Proceedings of 2nd International Conference on Information Science and Engineering.Hangzhou:IEEE,2010:5508-5511.

[9]BROOMHEAD D S,LOWE D.Multivarialble functional interpolation and adaptive networks[J].Complex System,1988,2:321-355.

[10]SPECHT D F.A general regression neural network[J].IEEE Transactions on Neural Network,1991,2:568-576.

[11]DING D X,ZHANG Z J.Artificial neural network based inverse design method for circular sliding slopes[J].J Cent South Univ Technol,2004,11(1):89-92.