一种提高重力坝抗震性能的方法
2011-05-03周星德吴继敏刘谦敏刘广波石星星
周星德,章 青,吴继敏,刘谦敏,刘广波,石星星
(1.河海大学力学与材料学院,江苏 南京 210098;2.河海大学地球科学与工程学院,江苏 南京 210098)
我国大型水工建筑物大多建于地震烈度高的西部地区,抗震设计要求高,所以需要对大坝进行动力反应和稳定性分析[1-2]。对于重力坝,侧重于深层抗滑稳定性研究,但目前大多基于静力分析[3-4],出现了界面元法、分项系数法、强度折减法等方法。坝体动力抗滑稳定性研究侧重于以下几个方面:坝基地震液化时的稳定性分析[5],动响应分析及最小动稳定性研究[6-8],坝体分段侧滑稳定性研究[9]。文献[10]针对上闸首结构进行了深层抗滑稳定性分析并绘制了动力抗滑稳定性时程曲线。但目前有关重力坝动力深层抗滑稳定性的研究还是偏少。
提高坝体稳定性的措施有:①将坝的迎水面做成斜面或折坡形坡面;②将坝基面开挖成倾向上游的斜面;③利用地形地质特点,在坝踵或坝趾设置深入基岩的齿墙;④采用有效的防渗排水或抽水措施,降低扬压力;⑤利用预加应力提高抗滑稳定性。上述措施主要通过增加坝体强度或减小外部力来提高坝体的稳定性。从结构抗震角度来讲,可通过附加阻尼装置或作动器来提高结构的抗震能力[11]。考虑到坝体属于大型结构,可采用在坝底铺设铅加球墨铸铁的方式来降低坝体动力反应。为此,笔者以某重力坝为研究对象,以实际地震波作为输入,研究重力坝深层抗滑稳定性。动力仿真结果表明在坝底铺设铅加球墨铸铁不仅可以降低坝体动力反应,而且提高了重力坝的深层抗滑稳定性。
1 动力分析模型
首先对重力坝计算区域进行有限元划分,假设结构阻尼为比例阻尼,则重力坝在地震作用下的运动方程可表示为

式中:X,﹒X,¨X分别为结点相对于坝基底部边界的位移矢量、速度矢量、加速度矢量;M,C,K分别为质量矩阵、阻尼矩阵和刚度矩阵;I为单位矩阵;¨xg为地震波加速度。
阻尼矩阵的计算公式为

式中:α,β为比例系数;ζ为阻尼比;ω1为坝体结构的第一阶固有频率(基频)。
计算坝体和库水的动力相互作用产生的动水压力时,可忽略库水的可压缩性,以坝面附加质量的形式计入。地震动水压力可折算为与单位地震加速度相应的坝面附加质量:

式中:Pw(h)为作用在直立迎水坝面水深 h处的地震动水压力;ah为水平向地震加速度;ρ为水的密度;H为总水深。
坝体材料模型采用弹塑性模型,屈服准则采用DP 准则,为

式中:I1,J2分别为应力第一不变量和第二偏应力不变量;k为仅与岩石内摩擦角φ和黏聚力c有关的试验常数。

式中:G eq为等效剪切模量;GmAx为最大剪切模量;γ为动剪应变;γr为参考剪应变,由动力剪切试验确定;A为基岩动力性质常数,A随着基岩的孔隙比、剪应变等因素而变化;τmax为抗剪强度。
2 深层抗滑稳定性分析
深层抗滑稳定性分析方法有应力代数和法、强度折减法、分项系数法等,本文采用应力代数和法,该方法通过有限元法计算求得应力场,根据应力结果合成求出滑移面上的阻滑力和滑动力,再通过投影合成求出滑体的抗滑稳定安全系数F。F的计算公式为

式中:下标i代表滑移面上单元的第i个结点;fi和ci分别为结点i的摩擦系数与黏聚力;σi和τi分别为结点i的法向应力和切向应力;li为结点i的代表面积(二维情况下为长度)。
3 实例分析
某重力坝坝高100m,顶宽10m,下游坡度为1∶0.6,上游水位为98 m,上游结构面与水平线的夹角为20°,下游结构面与水平线的夹角为40°。在坝体底部铺设厚度为1 m的铅加球墨铸铁,直接位于坝底部嵌入基岩中。模型中的基岩采用法向约束,有限元分析软件采用ABAQUS。
式(2)中,取 α=0,ζ=0.05,ω1=18.73 rad/s,则β=0.0053。坝体混凝土弹性模量为30GPa,密度为2500kg/m3,泊松比为0.167;基岩的弹性模量为15GPa,密度为 2700kg/m3,摩擦角为30°,黏聚力为1MPa,泊松比为0.22;结构面的弹性模量为15GPa,密度为2700kg/m3,摩擦角为27°,黏聚力为500kPa,泊松比为0.22;铅加球墨铸铁的弹性模量为145GPa,密度为7300kg/m3,泊松比为0。
地震波采用KOYNA波,持续时间为10 s,施加于外部边界线上。需要注意的是在确定位移、速度及加速度响应时,应减去外部边界处的对应值。静荷载作用时的Mises应力云图见图1,动力响应的最大位移(位于坝顶)、加速度(位于坝顶)、最大Mises应力(位于坝踵)响应时程曲线见图2~4。图5为稳定安全系数的时程曲线。
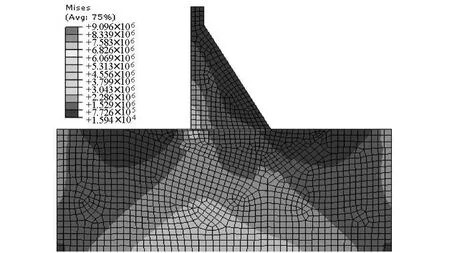
图1 静荷载作用时的Mises应力云图(单位:Pa)
由于铅加球墨铸铁的破坏强度达230MPa,而计算所得的应力仅为9.1MPa,所以不会产生破坏,这里,不考虑其应力分布。不铺设与铺设铅加球墨铸铁时的计算结果分别如下:坝踵处最大Mises应力为5.62mPa(4.87 MPa),坝顶最大水平位移为0.064m(0.061 m),F值小于2.5的概率为12.3%(8.41%),最小安全系数为2.13(2.27),其中,括号内的数值为铺设铅加球墨铸铁时的结果。可见,铺设铅加球墨铸铁可使最大Mises应力降低15%,最大位移降低5%,最小安全系数降低6.57%,F值小于2.5的概率降低3.89%。
4 结 语
目前,有关坝体深层抗滑稳定性动力分析的研究还较少,主要通过增加坝体强度或减小外部力来提高坝体的抗震稳定性,从结构抗震角度来提高坝体的稳定性尚未见报道。本文通过在坝底部铺设铅加球墨铸铁的方式来提高坝体的抗震能力,从而间接地提高重力坝的深层抗滑稳定性。从计算结果来看,铺设铅加球墨铸铁有效地减小了坝踵应力,降低了坝顶部最大响应,提高了坝体的深层抗滑安全系数。此外,铅加球墨铸铁的抗破坏能力很强,在重力坝底部铺设铅加球墨铸铁不会产生破坏。在构建坝体时,先铺设废弃的铅加球墨铸铁,虽然稍微增加了建设费用,但可提高坝体的抗震能力,这为提高大坝抗震性能提供了一种新的途径。

图2 坝顶水平位移响应时程曲线

图3 坝顶水平加速度响应时程曲线

图4 坝踵处Mises应力响应时程曲线

图5 稳定安全系数时程曲线
[1]颜天佑,李同春,郑治,等.索风营水电站Dr2危岩体稳定安全度有限元分析[J].河海大学学报:自然科学版,2009,37(6):691-696.
[2]陈松,陈志坚.软土地基上大型沉井基础安全监控模型[J].河海大学学报:自然科学版,2010,38(1):87-92.
[3]周伟,常晓林,徐建强.基于分项系数法的重力坝深层抗滑稳定分析[J].岩土力学,2007,28(2):315-320.
[4]王平,胡再强,田春亮,等.陶家沟尾矿坝三维静力和动力稳定性分析[J].水利与建筑工程学报,2010,8(1):53-55.
[5]严祖文,杨建民.坝基地震液化特性及动力稳定性分析[J].世界地震工程,2008,24(3):140-145.
[6]张晓燕,任旭华,邵勇.碾压混凝土重力坝陡峭建基面的动力稳定分析[J].红水河,2007,26(4):35-38.
[7]李周顺,何江达,苏向震,等.某重力坝坝体动力结构特性及坝基动力稳定性分析[J].四川水利,2008,30(1):13-17.
[8]周兵,金峰,王进廷.拱坝坝肩整体动力稳定性的离心模型试验[J].水利水电科技进展,2011,31(1):15-19.
[9]姚文生,周志广,陈伟韦.鞍钢矿业公司大孤山尾矿坝动力稳定性分析[J].岩土工程界,2009,12(12):65-68.
[10]胡婷,何力,韦先锋,等.亭子口上闸首结构静动力响应分析及深层抗滑稳定研究[J].灾害与防治工程,2010,68(1):33-37.
[11]周星德,林小国.非线性基础隔离结构振动控制研究[J].东南大学学报:自然科学版,2007,37(6):1023-1026.
[12]顾淦臣.土石坝地震工程[M].南京:河海大学出版社,1988.
