人工蜂群算法在渠道断面优化设计中的应用==pdf英文空格显示有误
2011-05-03苏国韶
钱 坤,苏国韶
(广西大学土木建筑工程学院,广西 南宁 530004)
在农田水利基础设施建设中,灌溉渠道建设费用占较大比重。渠道断面优化设计可有效地减少渠道的工程量,为工程建设节省大量投资。因此,渠道断面优化设计在渠道建设中具有重要作用。
常规的渠道断面优化设计一般采用试算法,该方法简单但需要反复试算,存在计算量大、累积误差大、计算精度不佳等缺点。为此,一些学者将无量纲分析法[1]、黄金分割法[2]应用于渠道断面优化中,取得了一定的成效,但渠道断面优化往往是一个非线性的多峰值优化问题,这些方法在搜索最优断面时容易陷入局部最优解。近年来,人们将遗传算法[3]、扩展微分进化算法[4]等全局智能优化算法引入渠道断面优化设计中,为获取全局最优解提供了可能。
蜂群算法是一种建立在蜜蜂自组织模型和群体智能基础上的新型智能优化算法,具有原理简单、全局性好、收敛速度快等特点,是当前优化研究领域的热点。目前,蜂群算法已被成功应用于函数优化、动态规划、车间调度等优化领域中[5-10]。迄今为止,蜂群算法已出现各种不同的版本,其中具有代表性的有Karaboga[11]提出的人工蜂群算法(artificial bee colony algorithm,简称 ABC算法)。研究表明,与遗传算法、粒子群优化算法、差分进化算法相比较,ABC算法在求解多变量、多峰值的全局优化问题上具有更好的适应性和鲁棒性[12]。
笔者拟采用ABC算法对梯形渠道断面进行多目标优化设计,寻求既考虑水力条件又考虑经济条件的最优断面,为渠道断面优化设计提供一种新的途径。
1 ABC算法
ABC算法是一种模拟蜜蜂种群采蜜过程的仿生算法。蜜蜂是一种群居生物,能够在复杂的环境下以极高的效率采集花蜜。研究表明,蜂群采蜜过程中,蜜蜂按任务角色分为3种类型:侦查蜂、精英蜂、跟随蜂,它们通过摇摆舞、气味等多种方式进行信息交流,协同完成采蜜任务。
ABC算法的基本原理是:将蜂群搜索最优花粉源的过程视为优化过程。首先,精英蜂分头寻找花粉源,跟随蜂在一个固定区域等待,精英蜂搜索到花粉后与周围的精英峰进行信息交流,选择花粉价值大的花粉源,然后回到固定区域,通过特定的舞蹈告知跟随蜂花粉源的价值大小,跟随蜂根据花粉源收益度的大小飞向相应的花粉源并在附近进行采蜜,花粉源的收益度越大则吸引的跟随蜂越多,以此提高蜂群搜索局部最优花粉源的能力;采完局部花蜜后,精英蜂继续搜索更好的花粉源,其中某些精英蜂始终无法搜索到更好的花粉源,则这些精英蜂飞出蜂群当前所在区域,成为侦查蜂,随机地飞向其他地方搜索更好的花粉源,以此来提高蜂群搜索全局最优花粉源的能力。通过这样一个分工协作寻找花粉源的过程,蜂群就能够以很高的效率在一定的搜索空间下获取最优花粉源。
ABC算法的具体实现步骤如下:
第1步 初始化:随机生成初始种群,初始种群的生成方法是从给定范围内随机选择,均匀分布于寻优空间。设精英蜂数量为Ne,跟随蜂数量为Ns,Ns=Ne,精英蜂群体Z={X1,X2,…,XNe},精英蜂个体 Xi={Xi,1,Xi,2,…,Xi,M},其中 i=1,2,…,N e,M为问题解的空间维数。X i∈R M,R M为精英蜂个体的集合,Xi的各个分量由式(1)产生:

式中:Xi,jmax,Xi,jmin分别为Xi的第j个分量的上限和下限;rand()表示0~1区间均匀分布的随机数。
初始跟随蜂的生成方法同精英蜂。设定由精英蜂生成侦查蜂的条件以及算法的收敛准则(误差允许值或最大迭代次数)。
第2步 计算种群每个个体的收益度ti:
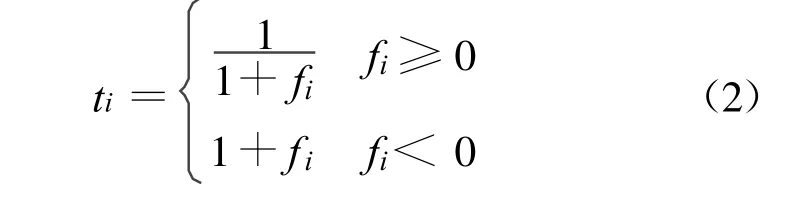
式中:fi为目标函数值。
进行精英蜂X i领域搜索,即通过式(3)产生新一代(第二代)精英蜂 Xi1:
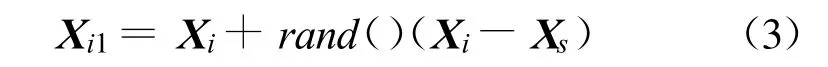
式中:X i,X s分别为上一代(第一代)2个不同的精英蜂个体,要求 i≠s。
第3步 计算第二代精英蜂每个个体的收益度ti,按式(4)分配精英蜂 Xi的跟随蜂数量,并由式(5)产生第三代蜂群Xi2:
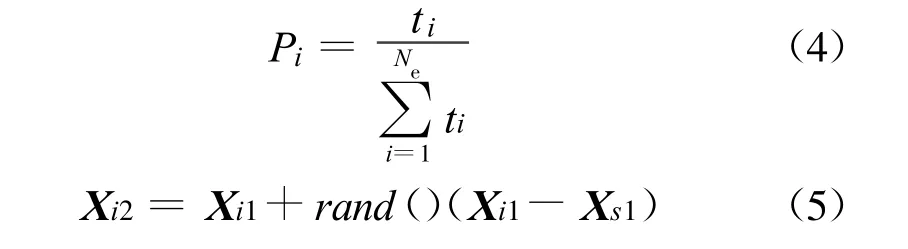
式中:X i1,X s1分别为第二代2个不同的精英蜂个体,要求 i≠s。
第4步 贪婪选择:计算新一代蜂群每个个体的收益度 ti,比较新一代蜂群个体与上一代蜂群个体的收益度大小,选择收益度大的个体组成新蜂群。
第5步 生成侦查蜂:经过贪婪选择后,对于收益度ti没有变化的次数达到设定值的精英蜂个体,按照式(6)变为侦查蜂X z i,X z i的各个分量为

第6步 不满足收敛条件时,返回第2步;反之,循环结束。
2 基于ABC算法的渠道断面优化
以某灌区的梯形断面渠道(图1)为例[4]进行断面优化设计,设计流量Qd=3.2m3/s,边坡系数m=1.5,渠道比降i=0.0005,渠床糙率系数n=0.025,渠道不冲流速vcs=0.8m/s,不淤流速vcd=0.4 m/s,求渠道底宽b和设计水深h的最优值。
对渠道断面优化问题进行数学建模,然后采用ABC算法进行求解。
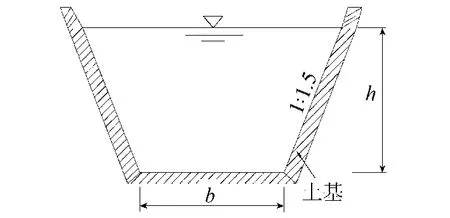
图1 渠道断面示意图
2.1 设计变量
梯形断面渠道设计一般按明渠均匀流进行水力计算,明渠均匀流公式为
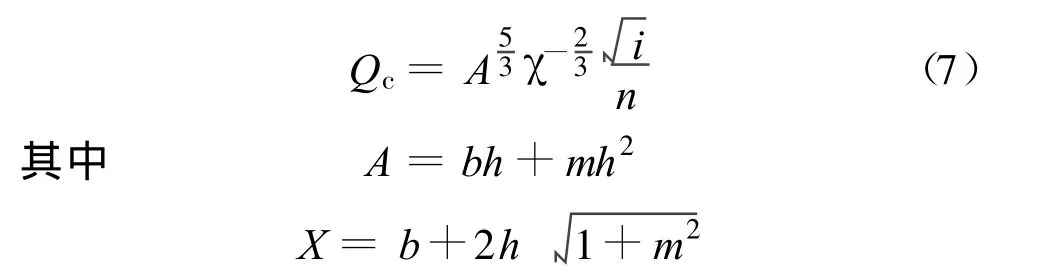
式中:Qc为渠道的计算流量,m3/s;A为渠道的过水断面面积,m2;χ为湿周,m。
在本算例中,渠道的m,n,i已知,b和h为设计变量。
2.2 目标函数
2.2.1 目标函数1
渠道断面优化同时满足2个目标:①计算流量接近设计流量(当Qc与Qd的差值微小时,认为断面的计算流量等于设计流量);②渠道过水断面的面积最小,以获得开挖工程量最小的经济断面。目标函数设为

式中:λ为平衡系数,作用是平衡式(8)右边2项的量纲与数值,本算例中,λ=10-5m-2。
目标函数1为复杂多峰值函数,见图2,给传统梯度优化方法获取全局最优解带来了较大困难。
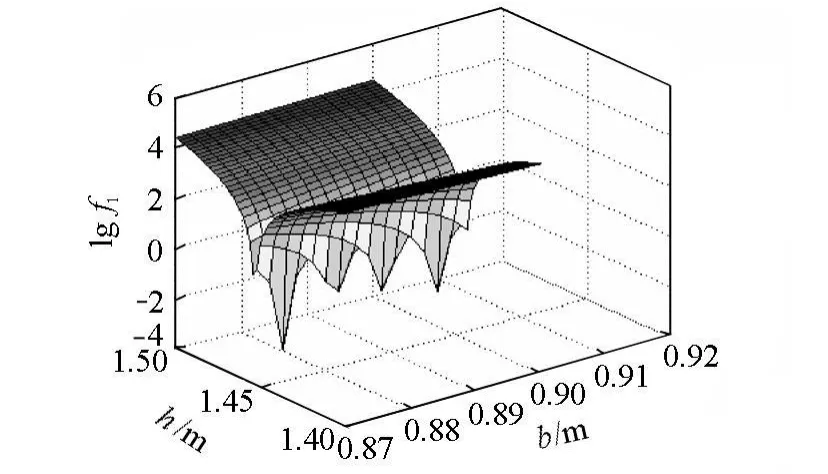
图2 目标函数1对数值的空间曲面
2.2.2 目标函数2
以满足流量条件为单一目标,目标函数设为

目标函数2也是一个复杂多峰值函数,见图3。

图3 目标函数2对数值的空间曲面
2.3 约束条件
渠道断面的平均流速值应在不淤流速vcd与不冲流速vcs之间;根据 m=1.5,符合规范的宽深比b/h的取值范围为(0.606,3.198),故目标函数1和目标函数2的约束条件均设为

2.4 ABC算法参数设置
ABC算法参数设置:维数M=2,种群总数N=10,精英蜂转化成侦查蜂的条件为:连续20次精英蜂的收益度ti不发生变化,精英蜂和跟随蜂的数量Ne=Ns=5。搜索范围:0.5m≤b≤5m,1 m≤h≤5m。收敛条件均设为<10-5。
约束条件处理:寻优过程中,当个体蜜蜂不符合上述约束条件时,其收益度加上大数进行惩罚;反之,按原收益度评价个体蜜蜂的品质。
2.5 计算结果
为了验证算法寻优的鲁棒性,反复计算20次。计算结果表明,采用ABC算法进行2个复杂多峰值函数优化时,20次计算的收敛成功率达到100%,说明ABC算法具有较高的寻优鲁棒性。渠道断面优化结果见表1。以目标函数的对数值作为纵坐标,目标函数对数值随迭代次数的变化曲线见图4、图5。

表1 渠道断面优化结果
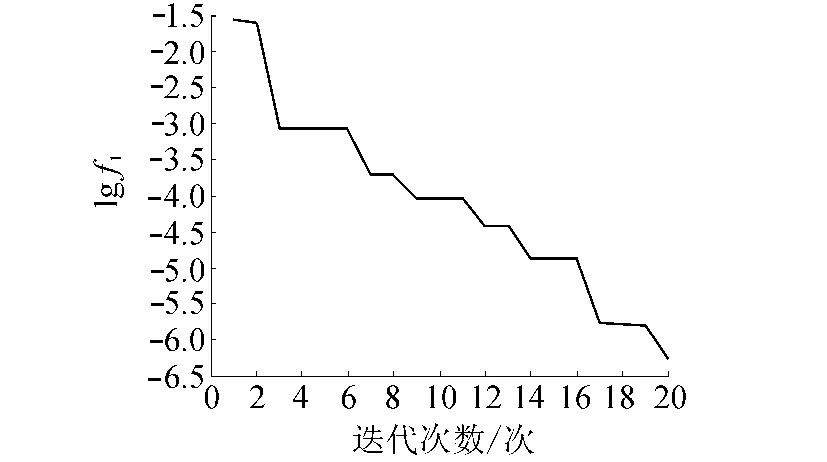
图4 目标函数1对数值的变化曲线
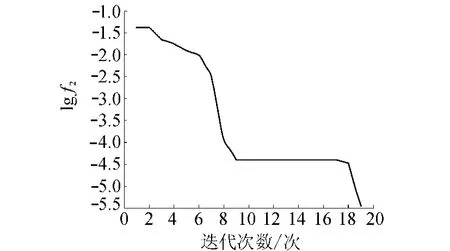
图5 目标函数2对数值的变化曲线
图4和图5表明,无论是目标函数1还是目标函数2,目标函数值随迭代次数下降的速度都非常快,说明了ABC算法的快速收敛性。
优化结果还表明,采用上述2种目标函数优化结果均满足断面的水力条件。与采用目标函数2相比,采用目标函数 1渠道过水断面面积减小了0.303 m2,说明采用目标函数1较为合理。
3 结 语
a.以梯形渠道断面为例,采用全局性好、鲁棒性强、收敛速度快的人工蜂群算法对渠道断面的流量和工程量优化问题进行求解,研究结果表明,该方法能获得令人满意的结果。
b.研究表明,既考虑水力条件又考虑经济条件的多目标优化结果较仅考虑水力条件的单目标优化结果更为合理。本文仅考虑渠道的单一断面优化,实际上,影响渠道工程量的因素还有断面形式、渠道比降、糙率系数、边坡系数等,关于复杂因素下渠道的优化设计将另文阐述。
[1]FLYNN E L.渠道断面优化设计[J].江西水利科技,1991,17(2):167-174.
[2]门宝辉,黄金柏,李树桥.黄金分割法在渠道断面设计中的应用[J].东北农业大学学报,2000,31(3):283-287.
[3]鲍卫锋,黄介生,孔祥元,等.基于遗传算法的渠道断面最优设计[J].中国农村水利水电,2005(5):75-78.
[4]倪士超,迟道才.基于扩展微分进化算法的渠道断面优化设计[J].人民长江,2009,40(13):81-82.
[5]BASTURK B,KARABOGA D.An artificialbee colony(ABC)algorithm fornumeric function optimization[C]//IEEE Swarm Intelligence Symposium 2006.Indianapolis:IEEE,2006.
[6]BASTURK B,KARABOGA D.A powerful and efficient algorithm for numerical function optimization:artificial bee colony(ABC)algorithm[J].Global Optim,2007,39(3):459-471.
[7]CHANG H S.ConvergingmArriage in honey-bees optimization and application to stochastic dynamic programming[J].Journal of Global Optimization,2006,35:423-441.
[8]KOUDIL M,BENATCHBA K,TARABET A,et al.Using artificialbees to solve partitioning and scheduling problems in codesign[J].AppliedmAthematics and Computation,2007,186(2):1710-1722.
[9]吴晶晶.基于人工蜂群算法的作业车间调度优化[J].郑州轻工业学院学报:自然科学版,2007,22(6):51-53.
[10]丁海军,李峰磊.人工蜂群算法在TSP问题上的应用及参数改进[J].中国科技信息,2008(3):159-161.
[11]KARABOGA D.An idea based on honey bee swarm for optimization,technicalreport[R].Turkey:Erciyes University,2005.
[12]BASTURK B,KARABOGA D.On the performance of artificial bee colony(ABC)algorithm[J].Appl Soft Comput,2008,8(1):687-697.
