SKM模型在天然河道的适用性研究
2011-05-03廖华胜李连侠蒋胜银芦妍婷
杨 华,廖华胜,李连侠,蒋胜银,芦妍婷
(1.四川大学水力学与山区河流开发保护国家重点实验室,四川 成都 610065;2.广东省水利水电勘测设计研究院,广东 广州 510610)
天然河道大多都是由滩地和主槽组成的复式河槽,其断面形状多不规则。滩、槽之间的动量交换[1]和边界阻力分布不均对水流的影响[2]使得天然河道的水流特性问题极为复杂。1991年,Shiono和Knight从黏性流体力学基本方程(N-S方程)出发,在恒定均匀湍流的前提下将方程简化进而提出SKM模型(Smono&Knightmodel)[3],其控制方程为

式中:ρ为水的密度;g为重力加速度;H为水深;S0为河道纵向底坡;f为摩阻系数;Ud为深度平均流速;s为河道边坡坡度;y为河道断面横向坐标;λ为无量纲涡黏性系数;Γ为二次流影响因子。
SKM模型提出以后,诸多学者利用其对形状规则的河槽进行试验和计算验证。王树东[4]对特定的复式断面进行水槽试验,分别针对不同水深进行流速分布的测量,证明SKM模型能够较为准确地估算明渠河槽横断面的流速分布。Liao等[5-6]对水位流量关系的理论解与单一矩形断面、对称两级复式断面和非对称两级复式断面水槽试验数据进行验证,证明SKM模型能够较精确地求得河槽水位流量关系,并且能分别给出主、滩槽的流量结果,可以考虑二次流的影响。
在实际工程求解析解的过程中,由于河道断面并不都是规则的单一或多级复式河槽,其横断面边界凹凸不平,在这种情况下,按断面形状规则的河槽来预测的过流能力与实际过流能力产生的误差较大,并且难以得到较精确的水位 流量关系,而数值方法在处理任意断面形状的问题时具有不可代替的优势。本文采用数值方法将SKM模型拓展到任意断面形状的水流模拟。
1 SKM模型数值模拟
1.1 数值模拟方法
对任意断面形状的河槽的水流模拟采用有限体积法(FVM)。FVM的基本思路是将计算区域划分为一系列不重复的控制体积,并使每个网格点周围有一个控制体积;将待解的微分方程对每一个控制体积积分,得出一组离散方程,其中的未知数是网格点上的因变量的数值;求解该线性方程组,即可得到节点上的值。为了求出控制体积的积分,必须假定未知数在网格点之间的变化规律,即假设未知数的分段分布剖面。
FVM的优点在于基本思路容易理解,并能给出直接的物理解释。该方法得出的离散方程要求因变量的积分守恒对任意一组控制体积都能得到满足,对整个计算区域,自然也能得到满足。
SKM模型的控制方程(1)可以写成:

可见,方程 (2)为一具有源项(S)、衰减项(衰减系数为E)和扩散项(扩散系数为D)的一般通用方程,其因变量为其FVM离散过程如下:
将方程(2)沿 y方向积分,得

将计算区域划分为有限个如图1所示的有限控制体,方程(3)对每个控制体均成立,可得出
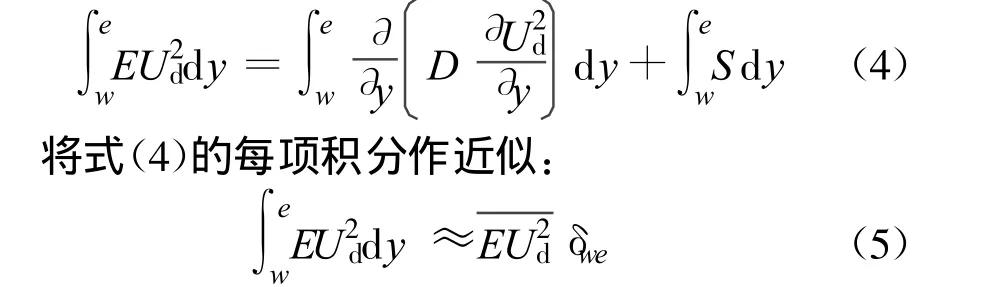
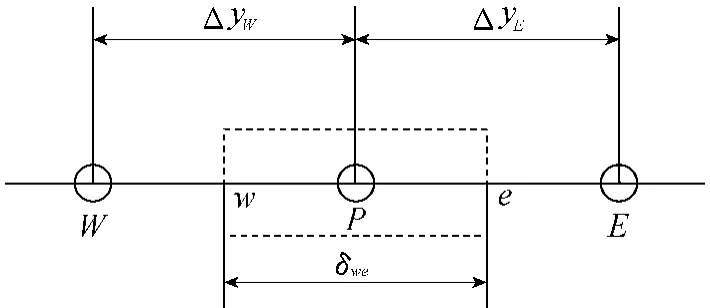
图1 有限控制体示意图

式中上划线表示在控制体内取平均值,可以简单近似为该控制体节点P处的值。将以上各近似表达式代入方程(4),得到以下离散方程:

式中:Dw,De为控制体界面上的值,在此采用其周围节点的调和平均值。
方程(11)就是利用有限体积法得到的SKM模型控制方程的离散方程,是一线性方程组,结合河道横断面两边边界条件,可采用解三对角矩阵的TDMA方法或 SOR迭代方法(本文采用该方法)求解。
1.2 参数确定
目前,可用于模拟天然河道流场的数值模型很多,如各种紊流模型等,这些模型的一大瓶颈便是水流特性参数如糙率的选取和确定。在紊流模型中,糙率只能通过修改壁函数的参数进行间接选取。SKM模型所涉及的3个参数为直接参数,物理意义更直观,且参数的选取目前已有较多的经验公式[7-8]。
摩阻系数f采用式(12)进行计算[9]:

式中:n为糙率;R为湿周。
对于参数 λ和Γ,采用芦妍婷等[10]根据大量水槽试验数据进行参数优化后得到的经验公式:
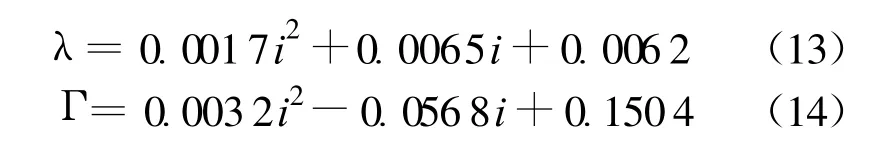
式中:i为河槽等效宽深比。
对任意断面形状的天然河槽,将横断面近似为等效矩形,求得近似宽深比后根据式(13)(14)求得参数λ,Γ后再进行适当的调整。
1.3 计算过程
本文进行数值模拟计算的程序(FVM&SKM)采用Compaq Visual Fortran 6.6编写。计算过程中,任意断面形状采用多线段进行近似,每一线段可以给定不同的参数值,有利于模拟具有主、滩槽的流动。计算直接对任意断面进行离散求解,相比紊流模型等其他模型简单实用。
得到深度平均流速Ud后,采用式(15)求解壁面阻力τ:

2 应用实例
为了验证SKM模型数值方法在天然河道应用中的可靠性与准确性,采用自编FVM&SKM程序对长江朱沱水文站(以下简称朱沱站)和英国特伦特河上Yoxall水文站(以下简称Yoxall站)的2个断面的深度平均流速及水位-流量关系进行计算,并与实测数据进行对比。
2.1 长江朱沱站计算结果及分析
朱沱站是国家重点水文站,位于长江上游,上距泸州60km,下距江津60km。作为三峡水库入库站,朱沱站是长江上游与三峡水库的水沙主要控制站之一。朱沱站测量断面形状如图2所示,朱沱站测量断面水位--流量关系对比见图3。水位分别为202.11m,207.16m时朱沱站测量断面深度平均流速侧向(y方向)计算与实测结果对比见图4,图4还给出了壁面阻力计算值。
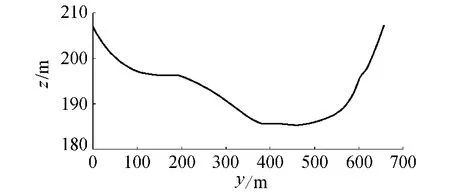
图2 朱沱站测量断面示意图
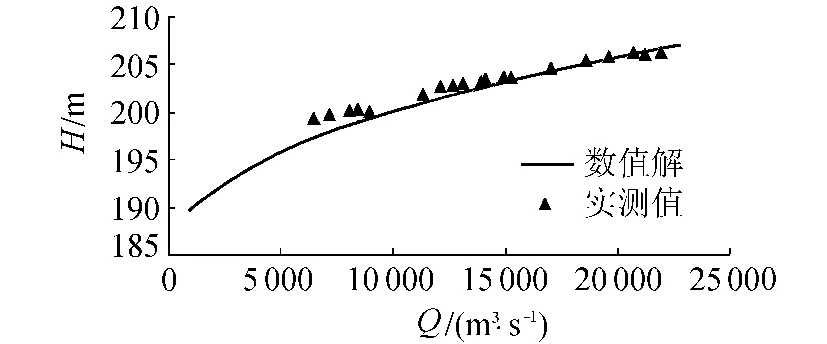
图3 朱沱站测量断面水位-流量关系对比
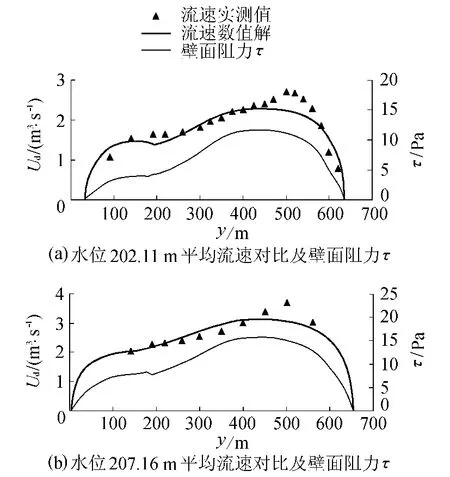
图4 朱沱站测量断面深度平均流速与壁面阻力
从图3可以看出,由数值模拟方法计算得到的朱沱站测量断面水位-流量关系与实测值吻合良好,表明数值模拟方法能较为精确地预测横断面水位流量关系,说明将该方法应用到实际工程的水位-流量关系预测中是可行的。由图4可知深度平均流速分布数值解与实测结果变化趋势相一致,在主河槽y=500m附近实测流速大于数值解,但总体吻合情况良好。壁面阻力τ在y=350~550m之间最大,与河床断面在该段冲刷最严重的实际情况相吻合,亦说明数值计算的深度平均流速结果是合理的。
2.2 特伦特河Yoxall站计算结果及分析
特伦特河[8]为英国英格兰中部河流,发源于斯塔福德郡,北流汇入亨伯河,全长274km,流域面积为1万km2。以位于英国特伦特河的Yoxall测量断面为例,该断面河槽是具有滩地的复式断面,滩地在河槽的左岸,断面形状如图5所示。图6为该河槽断面水位--流量关系对比。图7为水深分别是2.36 m,2.54 m时深度平均流速计算与实测结果对比,图7还给出了壁面阻力计算值。

图5 特伦特河测量断面示意图
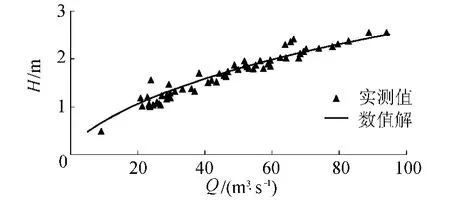
图6 特伦特河测量断面水位-流量关系对比
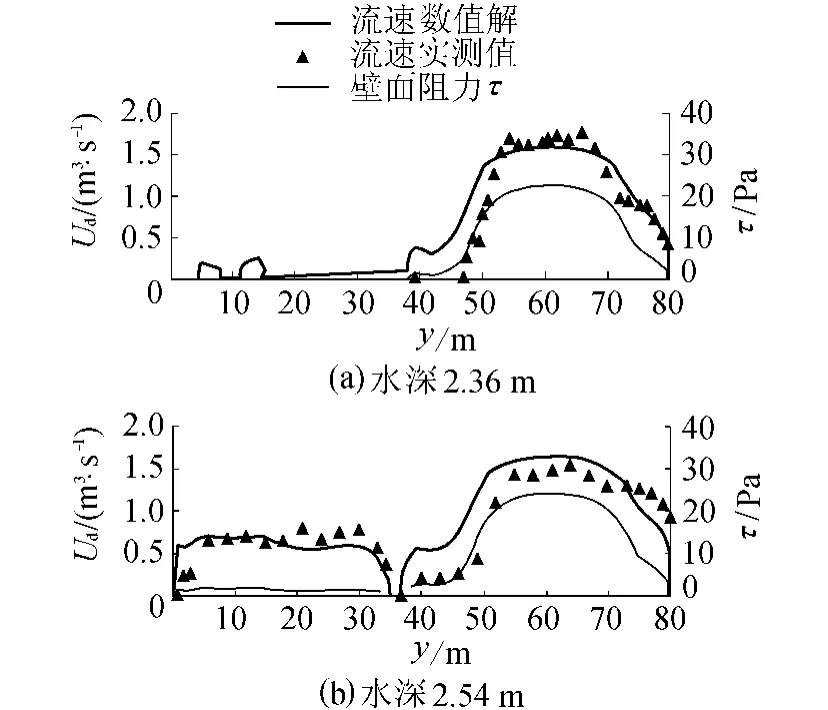
图7 Yoxall站断面深度平均流速与壁面阻力
由图6可以看出,数值计算的水位-流量关系结果与实测情况吻合良好。如图7(a)所示,当水深为2.36 m时,因河槽凹凸起伏,使测量断面处存在3个不连续的过水断面,其中在滩地处的2个过水断面面积几乎为零,计算更为复杂,如果采用解析解进行求解,难度可想而知。图7表明:在y=40~50m之间,由于河槽边壁形状较为复杂,无法精确模拟水流结构,但断面深度平均流速数值解与实测结果变化趋势一致,其他区域两者吻合情况良好;而壁面阻力τ在y=50m附近急剧增加,在y=70m附近快速减小,变化趋势与河床的冲刷情况一致。
3 结 语
实例应用结果表明,无论是水位-流量关系还是断面深度平均流速分布,SKM模型的FVM数值模拟结果与实测数据吻合良好,表明该方法在天然河道的适用性很强,计算结果可靠。该方法拓宽了SKM模型的应用范围,在河道过流能力、水位、洪涝范围等的预测方面具有实际应用价值。虽然目前已有很多较成熟的数值模拟手段,包括LES等精细模型可以用于模拟天然河道流场,但是计算成本随精度及分辨率的增加呈指数型增长,而SKM模型简单,计算运用方便高效。
[1]ZHELEZNYAKOV G V.Interaction of channel and floodplain streams[C]//Proceedings of 14th Conference of International Association for Hydraulic Research.Pairs:IAHR,1971:145-148.
[2]杨克君.复式河槽水流阻力及泥沙输移特性研究[D].成都:四川大学,2006.
[3]SHIONO K,KNIGHT D W.Turbulentopen-channel flows with variable depth across the section[J].J of Fluid Mechanics,1991,222:617-646.
[4]王树东.漫滩水流的二维流速分布及水力学计算[J].水利学报,1986,17(11):51-59.
[5]LIAO Hua-sheng,KNIGHT D W.Analytic stage-discharge formulas for fow in straight prismatic channels[J].Journalof Hydraulic Engineering,ASCE,2007,133(10):1111-1122.
[6]LIAO Hua-sheng,KNIGHT D W.Analytic stage-discharge formulas for fow in straight trapezoidal open channels[J].Advances in Water Resources,2007,30:2283-2295.
[7]ABRIL J B,KNIGHT D W.Stage-discharge prediction for rives in flood applying a depth-averaged model[J].J of Hydraulic Research,IAHR,2004,42(6):616-629.
[8]McGAHEY C.A practical approach to estimating the flow capacity of rivers[D].Milton Keynes:Open University,2006.
[9]吴持恭.水力学(上册)[M].北京:高等教育出版社,2003.
[10]芦妍婷,廖华胜.明渠流动S-K模型参数率定的随机搜索法[J].水利学报,2007,38(11):1364-1370.
