基于灰色理论的混凝土压缩损伤参数尺寸效应
2011-05-03王向东王跃锋岑家全
王向东,王跃锋,华 曦,岑家全
(河海大学力学与材料学院,江苏 南京 210098)
混凝土结构在浇筑过程中都有初始损伤,在外界因素如荷载、温度等作用下将产生新损伤和损伤积累,从而导致材料性能劣化,最终形成宏观裂缝直至整个结构破坏[1-2]。目前,混凝土的初始损伤、峰值损伤及损伤演变方程中的参数均是在实验室用标准小试件做试验测得,而工程中的结构特别是水工建筑物均是大体积混凝土结构,用上述损伤参数及损伤演变方程进行结构的损伤分析显然不合理[3]。因为混凝土的材料性能参数具有尺寸效应[4],损伤参数也与混凝土结构的尺寸密切相关,所以在混凝土结构的损伤分析计算中,必须考虑混凝土损伤参数的尺寸效应。而大试件的试验有相当的难度,因而解决混凝土损伤参数的尺寸效应问题非常必要。目前关于混凝土材料性能参数的尺寸效应问题已有许多研究,如混凝土材料的抗拉强度、抗压强度、弹性模量、断裂韧度、临界能量释放率和断裂能等[5],但是关于混凝土损伤参数的尺寸效应问题研究还很少。笔者拟对混凝土压缩损伤参数的尺寸效应问题进行研究。
1 混凝土损伤参数尺寸效应的试验研究
由于损伤是微观量,目前的实验设备不能直接测得,因此有必要将微观量宏观化,文中试验是在混凝土试件浇筑过程中掺入引气剂,人为制造随机微孔隙模拟损伤,并通过改变引气剂掺量达到模拟不同程度损伤的目的。对几组不同引气剂掺量的混凝土试件进行单轴压缩试验,测定弹性模量。通过弹性模量与引气剂掺量之间的关系曲线,计算混凝土理想无损弹性模量 E,同时测定多组不掺引气剂混凝土试件的弹性模量作为初始有效弹性模量[6]。
基于Lemaitre的应变等效假设,引入有效应力的概念,可以得到[7]

式中:D为损伤;E′为材料的有损弹性模量;E为材料的无损弹性模量。
D=0对应无损伤状态;D=1对应完全损伤(断裂或者破坏)状态;0<D<1对应不同程度的损伤状态[8-9]。在实验室测得多种尺寸小试件的有损弹性模量和无损弹性模量,由式(1)计算初始损伤D0和峰值损伤Df。
对不同尺寸的混凝土试件(截面为正方形)进行压缩损伤试验,得到截面尺寸分别为0.05m×0.05m,0.10m×0.10m,0.15m×0.15m和0.20m×0.20m的各柱形混凝土试件的初始损伤、峰值损伤(表1)。由表1可见损伤参数确实随试件尺寸的改变而变化,即混凝土损伤参数存在尺寸效应。
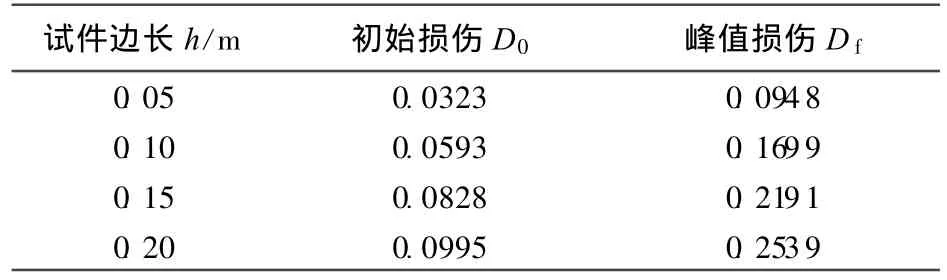
表1 4个不同截面尺寸试件的压缩初始损伤、峰值损伤
2 混凝土损伤参数尺寸效应的灰色理论研究
应用灰色理论,由小试件的试验数据预测较大尺寸试件的损伤参数,具体方法为:应用前期所做混凝土压缩损伤试验的结果,即不同尺寸试件的初始损伤、峰值损伤建立灰色预测GM(1,1)系统,预测较大尺寸试件的损伤参数;观察损伤参数的发展趋势,对损伤参数尺寸效应进行分析计算,以便进行混凝土结构的损伤分析及安全评价。
2.1 灰色预测模型概述
灰色预测模型是通过少量信息建立数学模型进行预测的一种方法。该模型所需建模信息少,运算方便,精度较高,在各种预测领域都有着广泛的应用,是处理小样本预测问题的有效工具。因此可以对混凝土压缩损伤参数建立预测模型,基于试验小样本数据进行大尺寸试件损伤参数的预测。

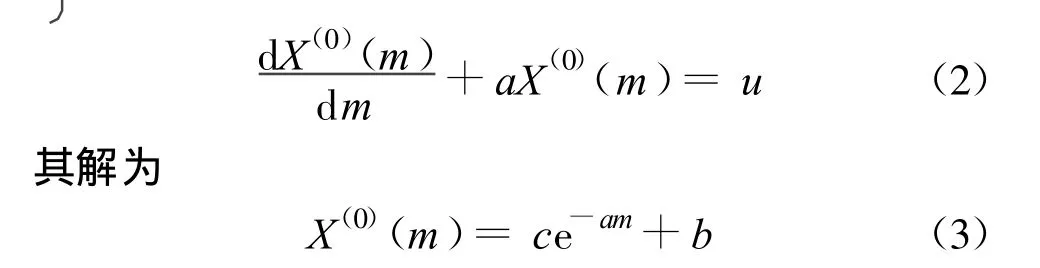
式中:a,u,c,b为参数,由式(4)和式(5)确定:
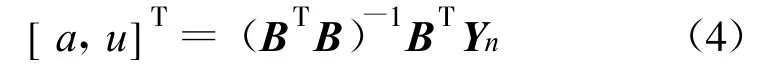

2.2 损伤参数的灰色预测模型
应用连续型GM(1,1)模型建立初始损伤的模型[12]。考虑到模型计算的便利,设试件边长为零时D0和Df均为零,由表1和式(6)、式(7)可得

最终得出初始损伤的灰色数值模型,即D0随 h的变化规律为

同理可以进行峰值损伤的灰色预测,Df随h的变化规律为
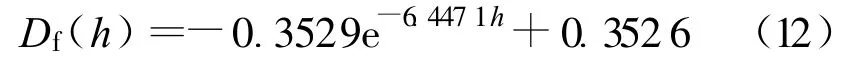
根据上述数值模型得到不同截面尺寸试件的初始损伤和峰值损伤,分别如表2、表3所示。由表2可见,初始损伤随着混凝土尺寸的增大而增大,最后收敛于一个固定值,根据式(11)可知该定值即为最大初始损伤0.1827。由表3可见,峰值损伤也随着混凝土尺寸的增大而增加,最后也收敛于一个固定值,根据式(12)可知该定值即为最大峰值损伤0.3526。

表2 不同尺寸试件的压缩初始损伤

表3 不同尺寸试件的压缩峰值损伤
将表2和表3中h=0.05~0.20m的计算结果与表1中的结果进行比较,最大误差小于2%,可见在现有的试验数据范围内,灰色预测模型具有很高的精度,据此预测的较大尺寸试件的损伤参数可应用于大尺寸结构的损伤分析。
3 结 语
混凝土损伤参数具有尺寸效应,在混凝土结构的损伤分析中应考虑混凝土损伤参数的尺寸效应。运用灰色理论对混凝土压缩损伤参数的尺寸效应进行研究,建立预测方程,以小试件初始损伤和峰值损伤试验数据为基础,预测较大尺寸试件的初始损伤和峰值损伤,推测了大体积混凝土的初始损伤和峰值损伤,得出如下结论:损伤参数虽然随混凝土尺寸的增大而增大,但最终趋近于一个固定值,初始损伤趋近于0.1827,峰值损伤趋近于0.3526,该值可用于大体积混凝土结构的损伤计算。
[1]徐道远,符晓陵,计家荣,等.拱坝破坏机理及损伤:断裂分析方法[C]//高拱坝学术讨论会论文集.北京:国家自然科学基金委员会工程与材料科学部,1996:208-217.
[2]徐道远,王向东,朱为玄,等.混凝土损伤及损伤仿真计算[J].河海大学学报:自然科学版,2002,30(4):14-20.
[3]周栋.混凝土材料性能尺寸效应[D].南京:河海大学,2003.
[4]曹亮.三点弯曲试件混凝土KIC尺寸效应公式的修正[J].河海大学学报:自然科学版,2007,35(1):63-66.
[5]金玉,王向东,徐道远,等.基于无损弹塑性模型的混凝土损伤定量分析[J].河海大学学报:自然科学版,2003,31(6):659-663.
[6]王向东,徐道远,周栋,等.混凝土损伤参数的尺寸效应[J].合肥工业大学学报:自然科学版,2005,28(3):308-310.
[7]余天庆,钱济成.损伤理论及其应用[M].北京:国防工业出版社,1993:58-90.
[8]李兆霞.损伤力学及其应用[M].北京:科学出版社,2002:46-70.
[9]ANDREEV G.Brittle failure of rockmAterials test results and constitutive models[M].Rotterdam:Balkema A A,1995:1-5.
[10]邓聚龙.灰色预测与决策[M].武汉:华中科技大学出版社,2002:120-180.
[11]王向东,朱为玄,徐道远.灰色理论在预测混凝土性能参数长期值中的应用[J].河海大学学报:自然科学版,1999,27(6):64-67.
[12]岑家全.混凝土压缩损伤参数尺寸效应的数值分析[D].南京:河海大学,2010.
