湍流标量输运过程中的Schmidt数识别

朱 嵩,刘国华,程伟平,黄跃飞

(1.广东省电力设计研究院,广东 广州 510663;2.浙江大学建筑工程学院,浙江 杭州 310058;3.清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)

在湍流传质和传热过程中,浓度扩散系数和温度扩散系数不仅和流体的属性有关,而且和流动状态密切相关。由于湍流在时间上的非定常性和空间上的各向异性,因而浓度或温度的扩散系数是时间和空间的函数,所以相对于物性参数,扩散系数的取值相对较为困难。在湍流传质研究过程中,一般引入Schmidt数来表达湍流的扩散能力。Schmidt数是一个无量纲参数,定义为动量扩散和质量扩散之比。

由于湍流Schmidt数和具体的湍流场有较大关系,因而很多学者进行了大量的调查、试验和数学模型研究。Tominaga等[1]调查总结了射流、浊流、边界层羽流弥散和建筑物附近的流动中的湍流Schmidt数的经验取值,指出湍流Schmidt数对预测结果具有较大的影响,应该根据不同类型的流动具体研究。He等[2]采用RANS方法对在横流中的射流的湍流Schmidt数对射流混合的影响进行了研究,认为此情况下湍流Schmidt数取0.2能较好地符合试验数据。张晓航等[3]对无剪切湍流混合层中被动标量的扩散进行了数值模拟,结合烟粒子扩散风洞试验研究了不同Schmidt数对被动标量扩散的影响。Xu[4]研究了高Schmidt数弱扩散条件下湍流中被动标量的混合,计算中Schmidt数达到了1024,泰勒尺度雷诺数约为8。Dudukoviĉ等[5]研究了湍流Schmidt数对降液膜的质量传输率的影响,指出湍流雷诺数通过影响湍流谱来影响湍流Schmidt数,其主要原因来源于高频和低频湍流脉动对传热传质输运的不同影响。随着雷诺数的增大,不仅湍流强度增大,而且湍流谱从低频向高频移动,结果使得雷诺数对质量输运的影响不如对动量输运的影响大,最终使得湍流的Schmidt数随着湍流雷诺数的增大而增大。Flesch等[6]通过大范围气体示踪试验获得了大气边界层的Schmidt数(约为0.6)。Ojo等[7]采用水动力观测数据研究了湍流扩散过程及扩散系数的确定方法。在湍流Schmidt数识别方面的研究较少,Guo等[8]采用遗传算法估计了横流中的射流的变系数Schmidt数,取得了较好的结果。

笔者将从概率统计的角度,采用Metropolis-Hastings算法对湍流标量输运的Schmidt数进行识别,其中湍流和浓度耦合场的求解采用有限单元法,湍流场求解采用Boussinesq涡黏性假设。采用Metropolis-Hastings算法识别流动输运参数参见文献[9-12]。

1 数学模型

湍流计算采用稳态标准 k-ε模型,浓度场计算采用非稳态对流扩散方程,控制方程如下:

式中:ui为流速;xi,xj,xk分别为i,j,k方向的空间坐标;ρ为密度;p为压强;η为流体动力黏度;ηt为湍流运动黏度;k为湍动能;ε为耗散率;c为浓度;νt为湍流运动黏度;Dt为湍流扩散系数;Sc为湍流Schmidt数;c1,c2,σk,σε为k-ε模型系数。

2 参数识别算法

Metropoils-Hastings算法是由Metropolis提出并由Hastings发展完善起来的一种概率抽样算法,属于马尔科夫链蒙特卡罗方法的一种。它是一种随机优化算法,通过随机游走的方式在Metropolis-Hastings准则下获得未知参数的样本,在对后验样本统计的基础上获得未知参数的估计值。结合湍流Schmidt数识别,提出参数识别算法如下:

第1步:构造正态分布似然函数作为湍流Schmidt数随机优化的目标函数。

第2步:在先验范围内随机产生湍流Schmidt数的初始值。

第3步:采用有限单元法和标准 k-ε模型计算当前湍流Schmidt数Scnow的似然函数值Lnow。

第4步:对当前湍流Schmidt数进行一个无偏扰动,获得湍流Schmidt数新的测试值Sctest,计算在测试值时的似然函数值Ltest。

第5步:如果 L test大于 L now,那么用 Sc test取代Scnow。

第6步:如果 Ltest小于Lnow,那么产生1个[0,1]区间的均匀分布的随机数m,如果 m小于Ltest和Lnow的比值,那么亦用Sctest取代 Scnow。

第7步:返回第 4步,反复迭代直到预定的次数。

第8步:对所有随机产生的样本进行统计以获得湍流Schmidt数的估计值。

3 算例研究

3.1 流动正问题的参数设置

取一个扩散器内的二维湍流扩散为算例。如图1所示,具有一定浓度的流体从左边界流入、右边界流出,边界条件设置见表1。进口流速为0.1m/s,进口浓度为1 mol/m3,瞬态计算总时间为20 s,时间步长为 0.1 s,运动黏度为 10-6m2/s。共剖分了2307个二次拉格朗日型三角形单元。

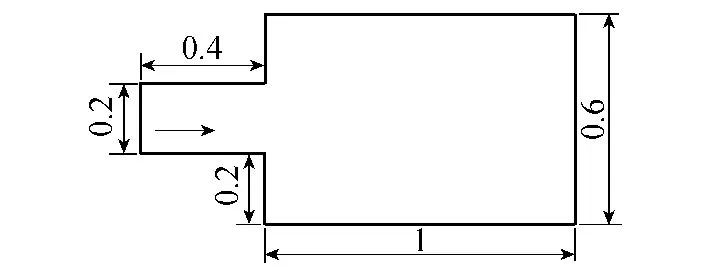
图1 二维湍流扩散流动计算域(单位:m)

表1 边界条件设置

以下取不同的湍流Schmidt数进行非稳态的浓度场计算。计算发现,不同湍流Schmidt数对标量场的时空分布有较大的影响。在相同的射流场内,当湍流Schmidt数较小时,射流浓度分散性较大,对流作用较弱;当湍流Schmidt数较大时,射流浓度较为集中,扩散作用较弱。由此可以看出标量场对湍流Schmidt数的敏感性较强,因而湍流Schmidt数具备良好的可识别性条件。

3.2 参数识别

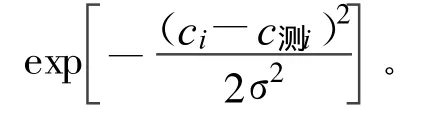
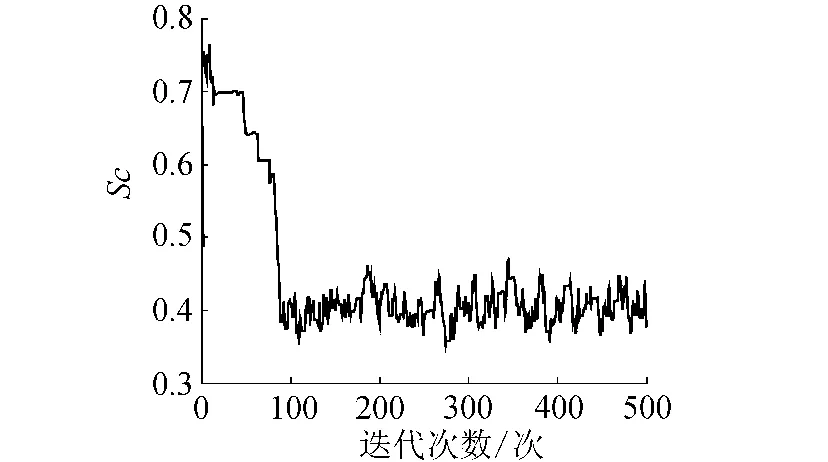
图2 湍流Schmidt数的迭代过程

图3 湍流Schmidt数的后验概率直方图

从图2中可以看出,马尔科夫链随机游走经历过一个初始化阶段(迭代大约100次)后进入了统计收敛域,表明计算参数的选取是合理的。为了验证计算结果的正确性,对迭代100次以后的400个抽样样本进行统计,样本均值为0.40498,均值的估计误差为1.245%,标准差为0.02199,均值95%置信区间为[0.40282,0.40715]。由此可以看出基于Metropolis-Hastings算法和有限单元法的参数识别方法识别精度较高。此外,从图3中可以看出,湍流Schmidt数后验分布具有较好的正态分布性质,其可识别性和识别精度都较高。

4 结 语

为了对湍流输运过程中的关键控制参数进行识别,提出基于Metropolis-Hastings算法和有限单元法的参数识别方法,湍流计算采用标准k-ε模型,标量场计算采用非稳态对流扩散方程。算例计算结果表明本文提出的算法能对湍流Schmidt数进行可靠的识别。

[1]TOMINAGA Y,STATHOPOULOS T.Turbulent Schmidt numbers for CFD analysis with various types offlow field[J].Atmospheric Environment,2007,41(37):8091-8099.

[2]HE Guang-bin,GUO Yan-hu,HSU A T.The effectof Schmidt number on turbulent scalar mixing in a jet-in-crossflow[J].International Journal of Heat andmAss Transfer,1999,42:3727-3738.

[3]张晓航,许春晓,张兆顺.Sc数对湍流被动标量扩散的影响[J].工程力学,2004,21(3):36-39.

[4]XU Shu-yi.Turbulent mixing of passive scalars at high Schmidtnumber[D].Georgia:Georgia Institute of Technology,2005.

[5]DUDUKOVIĈA,PJANOVIC R.Effect of turbulent Schmidt number onmAss-transfer rates to falling liquid films[J].Ind Eng Chem Res,1999,38:2503-2504.

[6]FLESCH T K,PRUEGER J H,HATFIELD J L.Turbulent Schmidtnumber from a tracer experiment[J].Agricultural and Forest Meteorology,2002,111(4):299-307.

[7]OJO T O,BONNER J S,PAGE C.Studies on turbulent diffusion processes and evaluation of diffusivity values from hydrodynamic observations in Corpus Christi Bay[J].Continental Shelf Research,2006,26(20):2629-2644.

[8]GUO Yan-hu,HE Guang-bin,HSU A T.Application ofgenetic algorithms to the development of a variable Schmidt number model for jet-in-crossflows[J].International Journal of Numerical Methodsfor Heat and Fluid Flow,2001,11(8):744-761.

[9]朱嵩,毛根海,刘国华,等.利用贝叶斯推理估计二维含源对流扩散方程参数[J].四川大学学报:工程科学版,2008,40(2):38-43.

[10]朱嵩.基于贝叶斯推理的环境水力学反问题研究[D].杭州:浙江大学,2008.

[11]朱嵩,刘国华,王立忠,等.水动力-水质耦合模型污染源识别的贝叶斯方法[J].四川大学学报:工程科学版,2009,41(5):1-6.

[12]朱嵩,毛根海,刘国华,等.改进MCMC方法及应用[J].水利学报,2009,40(8):1019-1023.