Markov链使用模型的测试用例生成方法研究

雷 航，陈丽敏

(1. 电子科技大学信息与软件工程学院 成都 610054; 2. 电子科技大学计算机科学与工程学院 成都 610054)

软件测试是软件开发的重要步骤和软件质量保证的重要环节。就其目的而言，软件测试可以分为两类：1) 通过测试发现错误，并不断改正错误，以期得到高质量的软件；2) 统计学的方法测试软件的可靠性(reliability)。

基于模型的软件测试属统计测试的范畴，要求基于软件的使用模型产生测试用例对软件系统进行测试。根据统计测试结果，可以估计被测软件的可靠性[1]，因此软件统计测试也称为软件可靠性测试。

软件的使用模型以一种形式化的方式表现出来，如有限状态机、UML模型和Markov链。模型是对软件使用情况的形式化建模，因此对测试的自动化起着重要作用。基于模型的软件测试，主要是面向测试的自动化。目前，基于模型的软件测试研究主要集中在软件测试模型本身的研究，即如何针对不同类型的软件提取专用模型，又可从专用模型中抽象通用模型。而在测试用例生成方面，由于在以往的测试用例生成中主要采用边界值、等价类划分等分析方法，用于手动生成测试用例，而该类分析生成测试用例的方法不利于测试用例的自动生成。本文针对上述问题，在基于模型的测试用例自动生成方法上进行研究。

1 软件使用模型

1.1 概述

软件模型是对软件的行为和结构的一种抽象描述，软件行为的描述方式有系统输入序列、活动、条件、输出逻辑和数据流等。软件结构可以使用组件图、部署图进行描述。针对不同的测试任务，对软件结构和功能进行抽象，并且用易于理解的方式进行描述，所获得的模型即是对被测软件系统精确的建模[2]，可以用于软件测试。一般根据软件的不同行为，采用不同的模型对软件进行描述，如程序依赖图、数据流图和控制流图表达了程序和代码结构间的行为关系，决策表和状态机则可以描述软件的外部行为。

基于模型的软件测试可以根据软件行为模型和结构模型生成测试用例。目前的软件规模庞大，使基于程序的测试十分困难，而基于模型的软件测试方法不仅可以有效地提高测试效率[3]及测试用例生成的自动化程度，进行测试失效辨识，也有利于评价测试结果。

1.2 Markov链使用模型

软件测试中使用的典型模型包括有限状态机、UML模型[4]和Markov链等模型。

Markov链[5]是一种以统计理论为基础的统计模型，在软件统计测试中得到了广泛的应用。它是一种迁移具有概率特征的有限状态机，可以根据状态间迁移概率自动生成测试用例，还可以分析结果，对软件性能指标和可靠性指标等进行度量[6-7]。另外，Markov链模型适用于对多种软件进行统计测试[8]，并可以通过仿真得到状态和迁移覆盖的平均期望时间，有利于在开发早期对大规模软件系统进行测试费用和时间的规划。

本文涉及的Markov链均为“有限状态、离散参数、时间齐次”。由Markov链描述的软件使用模型可以用随机迁移矩阵或带迁移概率的状态迁移图表示。

一个简单的软件Markov链模型如图1所示，该模型以迁移带概率特征的状态迁移图表示。

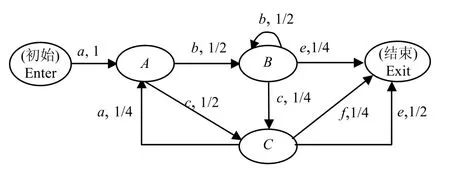
图1 Markov使用模型

图1中的节点代表使用状态(状态是指软件在t时刻的运行状态)向弧表示状态之间的转移，每条弧上都有一个激励(输入)与之对应，并指定了对应的概率，表明在当前的状态下输入激励，使软件转移到下一个状态，转移概率之和应为1。

每一个使用模型都有唯一的初态和终态。初态是每一次模型使用的开始状态，终态是模型使用的终止状态，是软件每一次使用的终结。软件的每一次使用即每一次操作都从初态开始，经过若干个中间状态，最后到达终态。

一条从最初的起始状态到终止状态的路径(历经的状态和弧序列)反映了软件的一次运行。每一状态转移对应一次输入，即一次激励。由于模型中可能有循环，会产生无穷序列。输入序列可以通过遍历状态转移图得到。利用软件的Markov链使用模型可以获得大量的输入序列。一个测试输入就是根据Markov链使用模型从输入域中随机产生的一个有限输入序列。

2 基于模型的测试用例生成

在基于模型的软件测试中，测试用例的生成方法取决于所采用的模型。以有限状态机模型为例，被遍历路径中弧的标记构成的序列即是测试用例。在构造满足测试准则的路径时，必须考虑约束条件，如路径长度限制，统计测试时还要考虑迁移概率[3]。

在Markov链表示的软件使用模型中，生成测试用例是在每一状态处不断选择激励，从而选择下一个输出状态的过程。常用的激励选择方式采用完全随机方法选择当前激励。运用该方法，理论上生成的激励均匀分布。

假设已得到某软件的Markov链模型，在常用的随机方法的基础上，考虑Markov链的状态迁移概率，在激励随机选择时加入一定的约束，使激励选择更符合软件的实际使用，使测试用例更有效。该算法将遗传算法中用于选择种群的选择算子——轮盘赌选择算子用于对激励进行选择，根据使用模型中状态间的转移概率选择激励，从而得到软件的下一状态。

根据Markov链的测试充分性准则[9]要求，测试过程中测试用例的迁移覆盖率与Markov链使用模型中的迁移概率相同[10]。

轮盘赌选择算子对激励进行的随机性选择符合软件实际使用的随机性，使所选激励出现的概率与软件实际使用中该输入产生的概率一致，本文采用理论方法对此进行了证明。因此，该算法从根本上保证了基于Markov链的测试充分性准则要求。

2.1 轮盘赌算法

文献[11]提出的轮盘赌选择算子，是遗传算法中选择算子的一种。它是基于比例的选择(proportional model)，利用各个个体适应度所占比例的大小决定其子孙保留的可能性。

轮盘赌的整个赌盘被分为大小不同的一些扇面，分别对应着价值各不相同的一些赌博物品。当旋转着的赌盘自然停下时，其指针所指扇面上的物品就归赌博者所有。虽然赌盘的指针具体停在哪个扇面无法预测，但指针指向各个扇面的概率却是可以估计，它与各个扇面的圆心角大小成正比。圆心角越大，停在该扇面的可能性越大；圆心角越小，停在该扇面的可能性越小。

与此类似，在遗传算法中，整个种群被各个个体所分割，各个个体的适应度在全部个体的适应度之和中所占比例也大小不一，该比例值瓜分了整个赌盘盘面(盘面设为1)，它们也决定了各个个体被遗传到下一代群体中的概率。

若某个个体为i，其适应度为F，种群大小为M，则该选择算子的具体执行过程为：

2.2 测试用例生成算法

步骤1)～步骤3)为对轮盘赌算法改进。

在根据软件使用模型生成测试用例时：

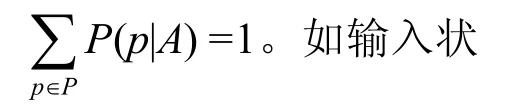
2) 产生0～1随机数序列，选取一种随机数生成方法，如利用计算机产生伪随机数序列。

3) 统计随机数落在各个子段的频率，频率最高的子段对应的元素被选中，即与子段对应的输出状态被选中。至此，转移的下一个状态被选出，即输出状态被选出。

4) 在下一输出状态处继续步骤1)～步骤3)，直到终止状态停止。

测试用例是从起始状态开始到达终止状态的状态和边(或激励)的序列。

不断从软件使用模型的初始状态开始，执行以上测试用例的生成过程，直到覆盖从起始状态到终止状态各路径的测试用例数目与状态转移概率相似时，停止测试用例生成。

2.3 算法有效性分析

根据伯努利大数定律：设X1,X2,…,Xn,…,相互独立都服从(0-1)分布随机变量。P{Xi=1}=p，P{Xi=0}=q(00，有：

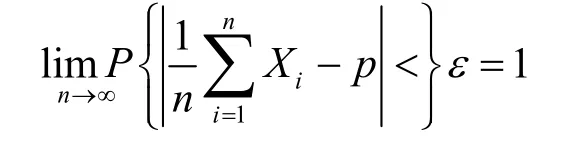
假设xi表示激励，软件目前状态为A，该状态的激励为一随机变量X，其取值为{x1,x2,x3}3种。激励的概率为Pk=P{X=xk,k=1,2,3}，以此类推。假设在N次随机数选择事件中，激励xk(k=1,2,3)被选中的次数为ak,ak/N为事件{X=xk}的频率。按照伯努利大数定理，当N充分大时，ak/N接近于Pk的概率等于1。因此，由模型得到的频率ak/N近似等于所求量Pk，说明频率收敛于概率。按该算法生成随机数序列，选中某一激励。在N次激励选择中，当N趋于某一值时，使该激励被选中的频率与期望概率近似相等，符合Markov链的测试充分性准则要求。

3 实验分析

3.1 实验过程

下面通过某软件的Markov链使用模型进行实例研究。

以图1为例，该Markov链使用模型由初始Enter、A、B、C、结束Exit共5个状态组成。

1) Enter状态仅有一个激励a，其概率为1，状态Enter输出状态集合为{A}。该激励映射区间为[0.00，1.00]。产生的0-1随机数序列均落在[0.00，1.00]区间内，因此其输出状态只能为A。此时的软件输出状态为A。

2) 对应A状态有b和c两个不同激励，其概率均为0.5。A状态的输出状态集合为{B,C}，将输出状态映射到[0.00,1.00]区间，具体为B对应区间为[0.00,0.50]，C对应区间为[0.50,0.10]。

3) 随机生成10个[0.00,1.00]区间的随机数，分别为0.389 697，0.294 927，0.225 976，0.150 322，0.358 294，0.688 660，0.122 489，0.905 322，0.844 990，0.766 531。

4) 统计得出落在[0.00,0.50]区间中的随机数为60%，落在[0.50,0.10]区间的随机数为40%。

区间[0.00,0.50]被选中的频率最高，所以选择B为输出状态。

5) 在输出状态B上执行步骤2)和步骤3)。对应B状态有b、c和e共3个不同激励，其概率分别为0.50、0.25、0.25。B状态的输出状态集合为{B,C,Exit}；将输出状态映射到[0.00,1.00]区间，具体为B对应区间为[0.00,0.50]，C对应区间为[0.50,0.75]，Exit对应区间为[0.75,1.00]。

随机生成10个[0.00,1.00]区间的随机数，分别为0.061 545，0.974 183，0.217 532，0.072 705，0.358 106，0.953 033，0.662 193，0.856 298，0.439 755，0.104 917。落在[0.00,0.50]区间中的随机数为60%，落在[0.50,0.75]区间的随机数为10%，落在[0.75,1.00]区间的随机数为30%。

区间[0.00,0.50]被选中的频率最高，所以选择B为输出状态。

6) 在B状态继续执行步骤2)和步骤3)。随机生成10个[0.00,1.00]区间的随机数，分别为0.668 492，0.483 965，0.092 351，0.996 575，0.273 176，0.409 635，0.890 488，0.638 671，0.736 871，0.884 251。落在[0.00,0.50]区间中的随机数为40%，落在[0.50,0.75]区间的随机数为30%，落在落在[0.75,1.00]之间的随机数为30%。

区间[0.00,0.50]被选中的频率最高，所以仍然选择B为输出状态。

7) 在B状态继续执行步骤2)和步骤3)。随机生成10个[0.00,1.00]区间的随机数，分别为0.825 414，0.495 734，0.086 770，0.710 631，0.050 235，0.939 459，0.853 754，0.584 155，0.704 494，0.837 837。落在[0.00,0.50]区间中的随机数为30%，落在[0.50,0.75]区间的随机数为30%，落在[0.75,1.00]区间的随机数为40%。

区间[0.75,1.00]被选中的频率最高，所以选择C为输出状态。

8) 在C状态执行步骤2)和步骤3)，具体步骤略。最后选择Exit为输出状态。

至此，产生了一个完整的测试用例，如表1所示。

以上方法仅是示例，在实际生成测试用例过程中，可在[0.00,1.00]区间生成更多数目的随机数，根据选中区间选择激励，以便更准确地体现转移概率。

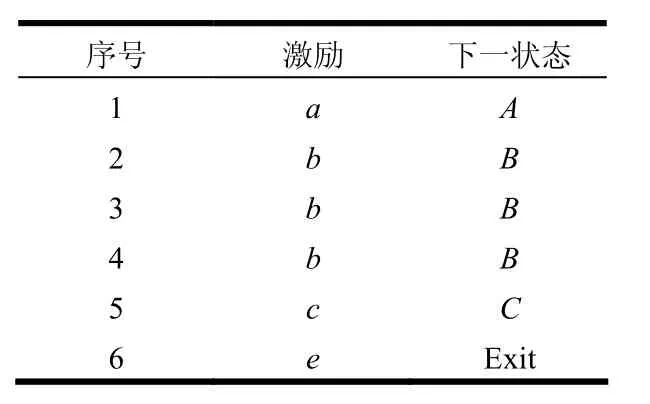
表1 测试用例示例

3.2 结果分析

以图1中C状态为例，E(C)={A,Exit}；P(C)={a,e,f}；F(C,a)=A，F(C,e)=Exit，F(C,f) =Exit；P(a|C)=1/4，P(e|C)=1/2，P(f|C) =1/4。利用完全随机方法和带概率约束的随机方法选择当前激励，激励被选中的频率如表2所示。

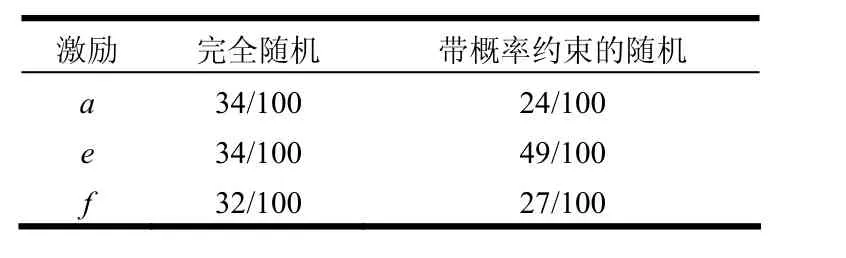
表2 结果对照

采用完全随机方法，激励被选择的概率比为34/100:34/100:32/100=1:1:0.941 2，采用带概率约束的随机算法，激励被选择的概率比为22/100:49/100:29/100=1:2.227 3:1.318 2。与P(a|C):P(e|C):P(f|C)=1/4:1/2:1/4=1:2:1相比，后者更接近软件Markov链使用模型中的转移概率比，由此可知，采用带概率约束的随机算法生成的测试用例更符合软件的实际使用。

4 结 束 语

测试自动化的意义重大，基于模型的测试用例生成为测试自动化打下了基础。本文通过采用轮盘赌选择算子，根据状态转移概率对激励进行选择，使生成的测试用例符合软件的实际使用。测试用例具有针对性，对提高软件可靠性具有重要的意义。

[1] JOHN D M. Software reliability engineering[M]. New York:The McGraw-Hill Companies, Inc. , 1999.

[2] 李军义. 软件测试用例自动生成技术研究[D]. 湖南: 湖南大学, 2007.LI Jun-yi. Research on techniques for software test case automatic generation[D]. Hunan: Hunan University, 2007.

[3] AVRITZER A, WEYUKER E J. The automatic generation of load test suites and the assessment of the resulting software[J]. IEEE Transaction on Software Engineering,1995, 21(9): 705-715.

[4] 颜炯, 王戟, 陈火旺. 基于UML的软件Markov链使用模型构造研究[J]. 软件学报, 2005, 16(8): 1386-1394.YAN Jiong, WANG Ji, CHEN Huo-wang. Deriving software markov chain usage model from uml models[J]. Journal of Software, 2005, 16(8): 1386-1394.

[5] HU Hai, JIANG Chang-hai, CAI Kai-yuan. Adaptive software testing in the context of an improved controlled Markov chain model[J]. IEEE on Computer Software and Applications, 2008, 32: 853-858.

[6] STACY J P, CARMEN J T, RICHARD C L, et al. 净室软件工程: 技术与过程[M]. 贲可荣, 张志祥, 张秀山, 等译.北京: 电子工业出版社, 2001.STACY J P, CARMEN J T, RICHARD C L, et al.Cleanroom software engineering: Process and technology[M]. Translated by BI Ke-rong, ZHANG Zhi-xiang, ZHANG Xiu-shan, et al. Beijing: Publishing House of Electronics Industry, 2001.

[7] POORE J H. Introduction to the special issue on:model-based statistical testing of software intensive systems[J]. Information and Software Technology, 2000,42(12): 797-799.

[8] 沙晓婷. 统计方法在软件测试中的研究与实现[D]. 北京:北京交通大学, 2008.SHA Xiao-ting. Research and implementation on software testing with statistical method[D]. Beijing: Beijing Jiaotong University, 2008.

[9] 高海昌, 冯博琴, 曾明, 等. 基于Markov链路径使用模型的软件统计测试[J]. 计算机工程, 2006, 32(19): 20-22.GAO Hai-chang, FENG Bo-qin, ZENG Ming, et al.Statistical software test based on Markov chain path usage model[J]. Computer Engineering, 2006, 32(19): 20-22.

[10] 沈海华, 卫文丽, 陈云霁. 覆盖率驱动的随机测试生成技术综述[J]. 计算机辅助设计与图形学学报, 2009,21(4): 419-431, 441.SHEN Hai-hua, WEI Wen-li, CHEN Yun-ji. A survey on coverage directed generation technology[J]. Journal of Computer-aided Design &Computer Graphics, 2009, 21(4):419-431,441.

[11] 王小平, 曹立明. 遗传算法——理论, 应用与软件实现[M]. 西安: 西安交通大学出版社, 2002.WANG Xiao-ping, CAO Li-ming. Genetic algorithmtheory, application and software implementation[M]. Xi’an:Xi’an Jiaotong Universiy Press, 2002.

[12] 马春燕, 胡飞, 张云鹏. 基于Markov链使用模型的组件复用的统计测试[J]. 计算机应用研究, 2008, 25(4): 1051-1053, 1056 MA Chun-yan, HU Fei, ZHANG Yun-peng. Statistical testing of component reuse using Markov chain usage model[J]. Application Research of Computers, 2008, 25(4):1051-1053, 1056