忆容器的Simulink模型及其主要特性分析

何朋飞，王丽丹，段书凯，李传东

(1. 西南大学电子信息工程学院 重庆 北碚区 400715; 2. 重庆大学计算机学院 重庆 沙坪坝区 400033)

1971年，文献[1]根据电路完备性理论，提出了忆阻器。2008年5月，HP实验室宣布制造了第一个物理实现的忆阻器[2]。2008年11月，在伯克利大学举行的忆阻器和忆阻系统国际研讨会上，定义了忆容器和忆感器两种记忆元件。与忆阻器相比，在数据读写和存储方面，忆容器丢失的数据更少。2009年10月，文献[3]对忆容器又做了进一步的研究，给出了忆容器的数学模型。

目前国内外针对忆阻器的研究较多，文献[4-6]研究了忆阻器的特性；文献[7-10]研究了忆阻器交叉阵列及在图像处理、混沌和存储中的应用。但对忆容器的研究较少，现有的关于忆容器的数学模型有基于分段线性函数的忆容器的数学模型[3]和仿照HP忆阻器的数学模型建立的Spice模型[11]两类。

本文介绍了忆容器的数学模型，建立了忆容器的Simulink模型，得到了忆容器的典型特性，验证了其有效性，探讨了参数以及输入激励对忆容器的影响。

1 忆容器的数学及Simulink模型

式中，C1和C2分别代表C的最小值和最大值；VT、α和β是常数；θ函数为单位阶跃函数。忆容器的电路符号如图1所示。

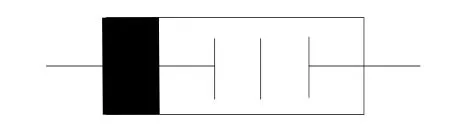
图1 忆容器的电路符号

根据式(3)和式(4)可建立忆容器的Simulink模型，如图2所示。

图2 忆容器的Simulink模型

2 输入激励和忆容器的各项参数对忆容器特性的影响

2.1 输入信号频率对忆容器特性的影响

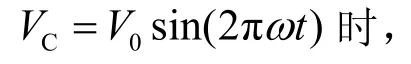
图3 信号频率对忆容器特性的影响

图3显示了输入不同频率的正弦信号得到的仿真结果，该结果反映了不同信号频率对忆容器特性的影响，其中，图3a、图3c和图3e中纵轴代表电容C，横轴代表电压VC(t)，图3b、图3d和图3f中纵轴代表电荷q，横轴代表电压VC(t)。从图3中可以看出，当输入信号频率变小时，忆容和电压曲线由一个圆环变成了一个有边界的磁滞曲线，这是由于随频率的变小，忆容器的容值会达到它的最大值和最小值。

2.2 输入信号幅度对忆容器特性的影响

2.3 α和β对忆容器特性的影响

2.4 输入不同波形对忆容器特性的影响

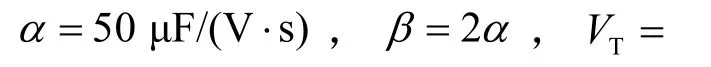
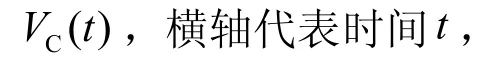
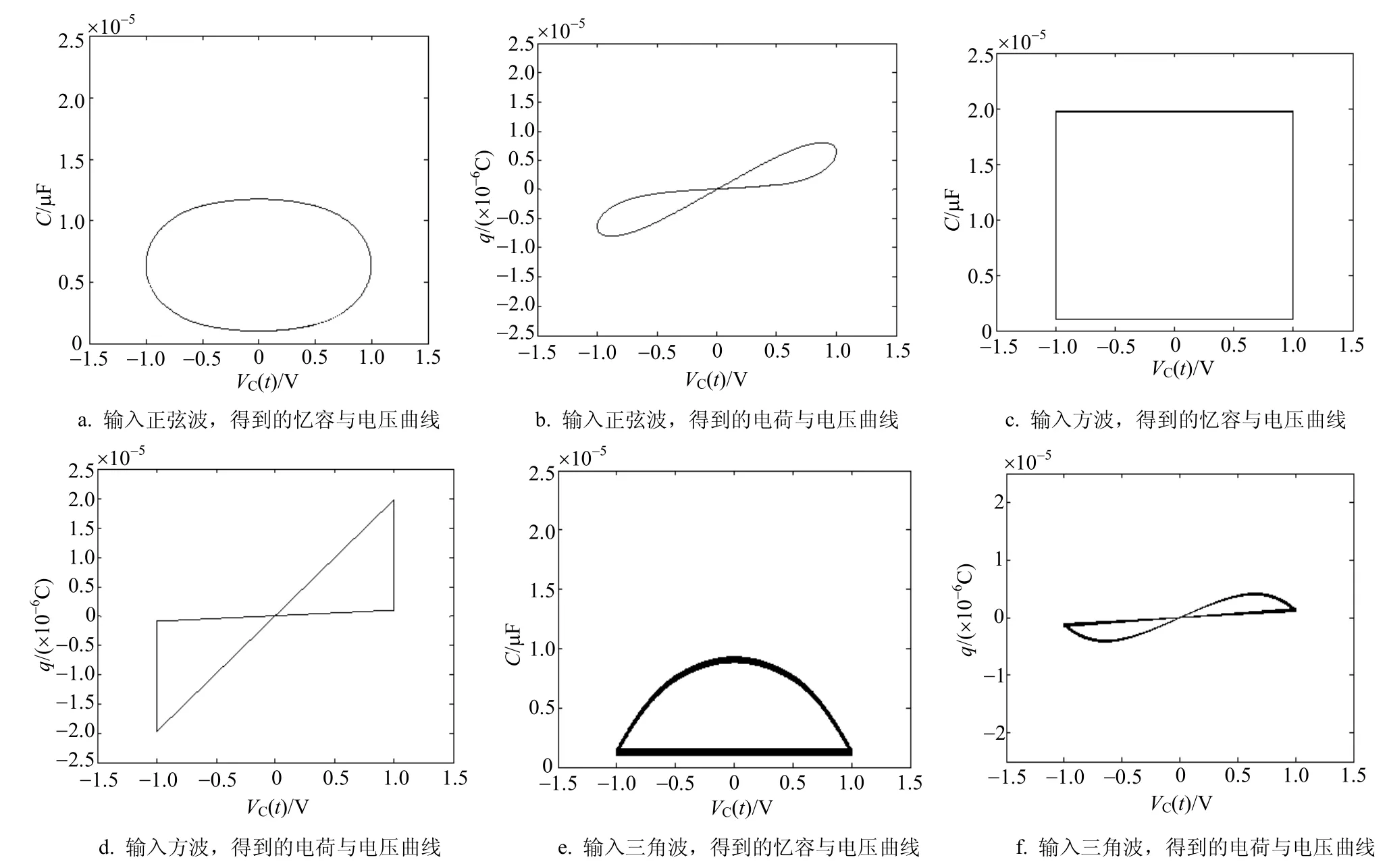
图4 波形对忆容器特性的影响

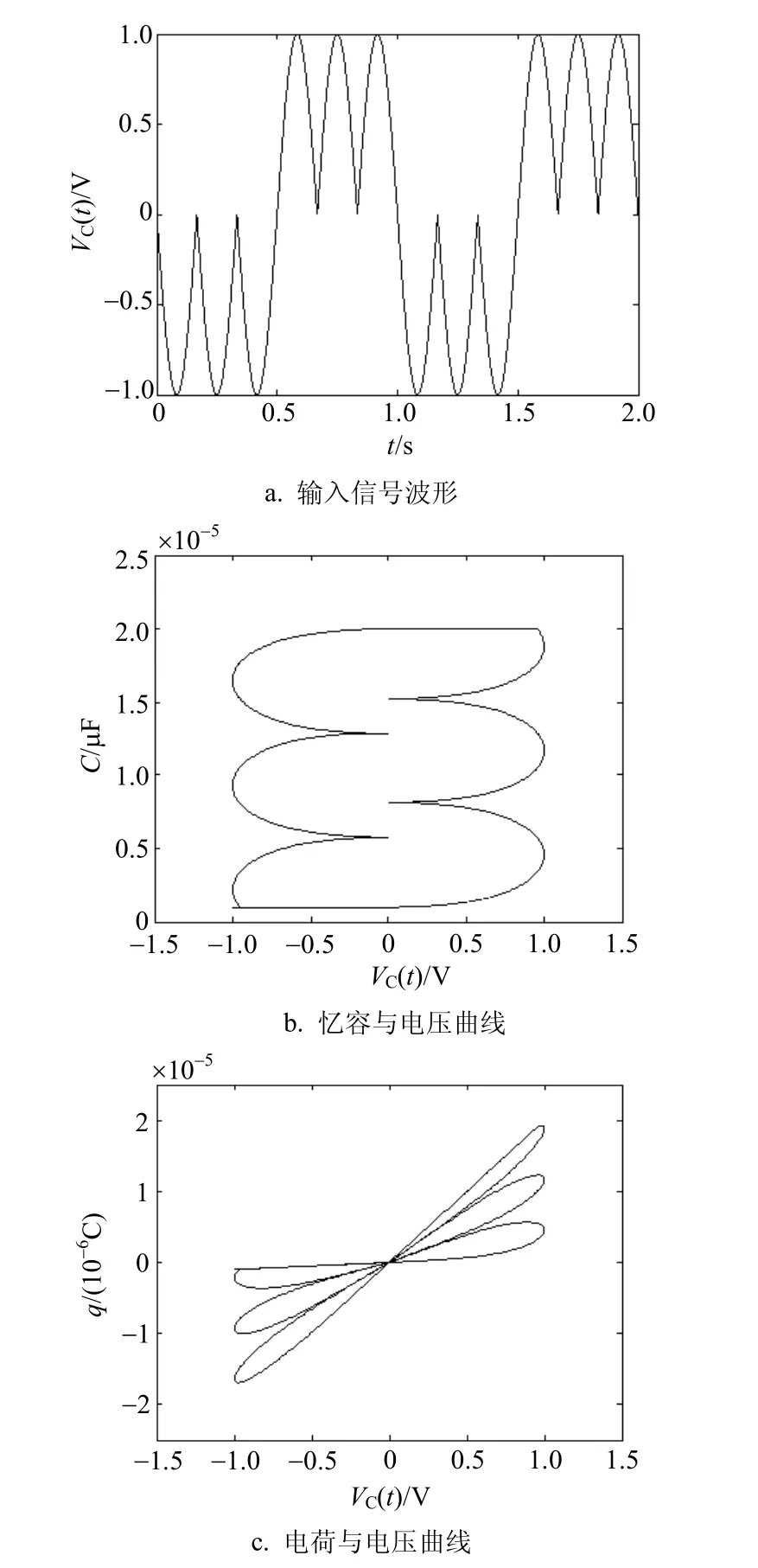
图5 波形对忆容器特性的影响

3 结 论

本文介绍了忆容器的数学模型，为了便于研究，根据其数学模型，建立了忆容器的Simulink仿真模型，对其仿真，得到了忆容器的典型特性，验证了该模型的有效性。研究了不同输入和忆容器参数对忆容器特性的影响，得到了许多忆容器的特性和一些重要的数据。这些研究成果为以后忆容器的研究奠定了一定的基础，特别是在其应用方面的研究，有望用于无线传感器网络，可以简化网络结构，并提高网络集成度。

本文研究工作得到西南大学博士科研资助项目(SWUB2008074)及西南大学教育教学改革研究项目(2009JY053, 2010JY070)的资助，在此表示感谢。

[1] CHUA L. Memristor-the missing circuit element[J]. IEEE Trans Circuit Theory, 1971, 18(5): 507-519.

[2] DMITRI B S, GREGORY S S, DUNCAN R S, et al. The missing memristor found[J]. Nature, 2008, 453(7191):80-83.

[3] MASSIMILIANO D V, YURIV V P, LEON O C. Circuit elements with memory: memristors, memcapacitors, and meminductors[J]. Proceedings of the IEEE, 2009, 97(10):1717-1724.

[4] DRAKAKIS E M, YALIRAKI S N, BARAHONA M.Memristors and bernoulli dynamics[C]//Cellular Nanoscale Networks and Their Applications(CNNA), 2010 12th International Workshop on. [S.l.]: [s.n.], 2010: 1-6.

[5] WANG Wei-dong, YU Qin, Xu Chun-xiang, et al. Study of filter characteristics based on PWL memristor[C]//International Conference on Communications, Circuits and Systems. Milpitas, CA: IEEE Press, 2009: 969-973.

[6] KAVEHEI O, KIM Y S, AZHAR I, et al.. The fourth element: insights into the memristor[C]//International Conference on Communications, Circuits and Systems.Milpitas, CA: IEEE Press, 2009: 921-927.

[7] 胡小方, 段书凯, 王丽丹, 等. 忆阻器交叉阵列及在图像处理中的应用[J]. 中国科学, F辑: 信息科学, 2011, 41(4):500-512.HU Xiao-fang, DUAN Shu-kai, WANG Li-dan, et al.Memristive crossbar array with applications in image processing[J]. Science in China Series F-Information Sciences (in Chinese), 2011, 41(4): 500-512.

[8] BHARATHWAJ M, PRACHETA P K. Memristor based chaotic circuits[J]. IETE Technical Review, 2009, 26(6):417-429.

[9] ITOH M, CHUA L O. Memristor oscillators[J]. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering, 2008, 18(11): 3183-3206.

[10] WITRISAL K. Memristor-based stored-reference receiverthe UWB solution[J]. Electronics Letters, 2009, 45(14):713-714.

[11] BIOLEK D, BIOLEK Z, BIOLKOVA V. Spice modelling of memcapacitor[J]. Electronics Letters, 2010, 46(7):520-522.