基于MUSIC算法的Pol-InSAR相位估计方法

张晓玲，陈 钦，韦顺军

(电子科技大学电子工程学院 成都 610054)

极化干涉合成孔径雷达(Pol-InSAR)技术能够全天时、全天候获取大面积数字高程图像(DEM)，是目前SAR遥感技术发展的重要方向。极化干涉合成孔径雷达不仅具有干涉合成孔径雷达(InSAR)对散射体的空间分布和高度的敏感性，而且还具有极化合成孔径雷达(PolSAR)对散射体的形状和方向的敏感性。Pol-InSAR通过极化和干涉信息的有效组合，可以同时提取观测对象的空间三维结构特征信息和散射信息，为微波定量遥感、高精度数字高程信息和观察对象细微形变信息的提取提供了可能性[1]。

传统的极化干涉SAR干涉相位估计方法是直接选取全极化数据的一个极化通道(如HH)，利用InSAR图像配准的方法进行干涉相位估计，得到配准偏移量后应用于所有极化通道进行插值重采样。由于极化组合方式不一样，各极化通道的配准偏移量存在微小的差别，直接以一个极化通道数据的偏移量为标准，将影响其他极化通道干涉相位估计的准确性。文献[2]提出了基于加权联合单像素模型的干涉相位估计方法，是目前InSAR干涉相位估计精度很高的方法之一，但在估计干涉相位时需要首先确定配准误差的大小和方向，并且确定最优权值时需要搜索，因此计算量较大。

本文提出一种基于MUSIC算法的多极化干涉相位估计方法，其基本思想是在Pol-InSAR图像粗配准的条件下，利用维纳滤波器[3]获得最佳滤波器参量(最优权值)；再利用该参量构造多极化联合最佳加权矢量，由该矢量获得协方差矩阵和相干系数矩阵；然后结合MUSIC算法[4]，特征分解协方差矩阵得到信号子空间和噪声子空间，根据两者的正交性构造空间谱函数，通过谱峰搜索准确地估计各极化通道的干涉相位。

1 多干涉相位估计模型

1.1 信号模型

在极化干涉合成孔径雷达系统中，单次双天线或重复轨道单天线测量得到的两个信号可以分别表示为：

在上面的接收信号模型中，为了准确地估计出各极化通道的干涉相位，各极化通道两幅图像的同一像素点i必须对应地面的同一散射体。而实际接收到的各极化通道SAR图像存在像素偏移，其相位差不能反映地面高度起伏的情况[5]。因此，首先进行各极化通道SAR图像配准过程。

1.2 多极化SAR图像精配准

干涉复图像对的配准基本上分为两个步骤：1) 进行粗配准[6-7]得到像素级的精度，对应的配准误差为一个分辨单元；2) 通过精配准得到亚像素级的精度，一般要求达到0.1～0.01分辨单元[8-10]。

各极化通道SAR图像经过粗配准后，针对同一像素点i，副图像较主图像配准误差为一个分辨单元，并且误差方向可能存在于副图像像素i上下左右的任一方向。本文利用维纳滤波[3]的相关理论，对各极化通道SAR图像数据精配准。在最小均方误差准则(MMSE)下，取副图像中相应像素点作为输入信号，对主图像像素i作最小均方估计。最后经维纳滤波得到的输出信号就为对主图像像素i精配准后的副图像相对应的像素点。

因为误差单元存在于副图像对应像素i上下左右的任一方向，所以取副图像中对应像素i的一个3×3(也可以选取5×5)的矩阵，作为维纳滤波器的输入信号，建立如下的维纳滤波器模型[3]：

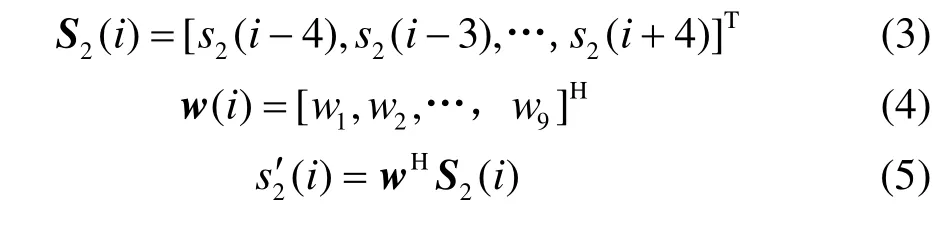
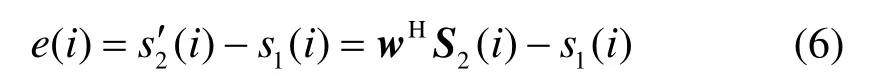
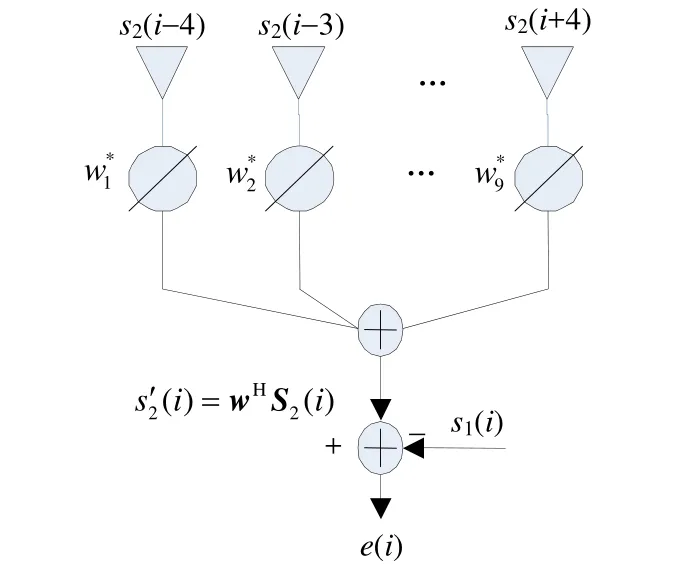
图1 维纳滤波器模型

式中，S2(i)是由副图像中对应像素i的3×3矩阵所构成的回波信号矢量；w(i)为对应的维纳滤波器参量；e(i)为主副图像对应像素点i的估计误差。根据最小均方误差准则，最佳的滤波器参量wopt(i)应使得性能函数——均方误差为最小：

利用维纳滤波理论对各极化通道SAR图像精配准过程中，因为误差单元就存在于副图像对应像素i的一个3×3矩阵里，只需要选取该3×3矩阵作为维纳滤波器的输入信号，就可以得到精配准后的副图像相应像素点。与文献[2]相比，本文所提方法不需要首先估计出配准误差的大小和方向，降低了这一过程的复杂性。并且对副图像每一像素点进行同样的操作，都可以得到主图像对应像素的最小均方估计，因此具有自适应图像配准功能。

1.3 干涉相位估计

根据前面的信号模型式(1)和式(2)，每个极化通道主副图像像素点i中含有相位噪声，利用维纳滤波实现各极化通道SAR图像精配准后，相位噪声仍存在于主副图像像素点i中。在图像精配准达到亚像素级精度的情况下，由于相位噪声的存在，主副图像直接共轭相乘估计干涉相位是不精确的。而精配准后利用MUSIC算法特征分解出信号子空间和噪声子空间，并且噪声子空间正交于信号子空间，因此具有很强的相位噪声抑制功能，可提高各极化通道干涉相位估计的精确度。

2 算法处理步骤

本文提出的基于MUSIC算法的多极化干涉相位估计方法，首先经过维纳滤波获得最佳滤波器参量，实现多极化SAR图像的精配准，然后利用该参量构造协方差矩阵，并结合MUSIC算法准确地估计出信号子空间和噪声子空间，再根据两者的正交性构造谱函数。图2是利用该算法估计多极化干涉相位的处理流程。

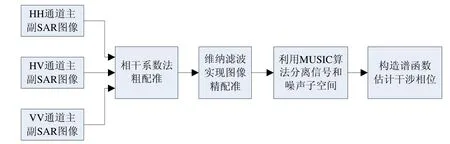
图2 本文算法处理流程

具体步骤如下：

1) 利用维纳滤波图像精确配准。

首先利用传统的相干系数法进行粗配准，使配准误差为一个分辨单元；接着通过维纳滤波器实现各极化通道SAR图像的精配准，达到亚像素级的精度。维纳滤波器中最佳维纳滤波器参量w(i)的求解方法如下(以HH通道为例)：

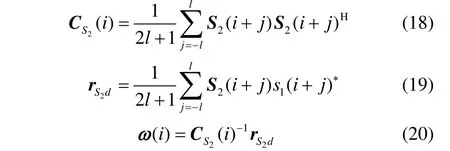
2) 估计信号子空间和噪声子空间。

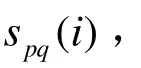
对各极化通道每一像素i执行上面的处理过程，就可以准确地估计出多极化通道干涉相位。

3 实验结果与分析

本文选用的极化干涉数据是PiSAR全极化(HH,HV, VV)干涉实测数据，实验中天线1的SAR图像(主图像)像素大小为550×450，天线2(副图像)像素大小为450×450。主图像和副图像的总体幅度图分别如图3a和图3b所示，图中对应像素存在明显的偏移，在进行干涉处理前需要对两幅SAR图像进行配准。

图3 HH通道幅度图

各极化通道SAR图像经过粗配准后，各极化通道的干涉相位图如图4所示。

图4 粗配准的极化干涉相位

图5 多极化干涉相位图

采用本文基于MUSIC算法的多极化干涉相位估计方法，得到的HH、HV和VV多极化干涉相位图如图5所示。对比图4和图5的相位图可以看出，本文干涉相位估计方法相对于粗配准算法可以获得更加清晰的干涉相位条纹图，并且极大地抑制了相位噪声，提高了干涉相位图的质量。

干涉相位图残差点数[13]是衡量干涉相位图质量的主要指标之一，残差点数过多容易导致后续相位展开失败而无法获取地形高程。经过图像配准后，残差点数越少则证明配准精度越高。为了比较图像配准精度，对相干系数粗配准法、文献[2]中方法及本文方法获取的干涉相位图进行残差点统计，得到的不同极化干涉相位中的残差点数如表1所示。

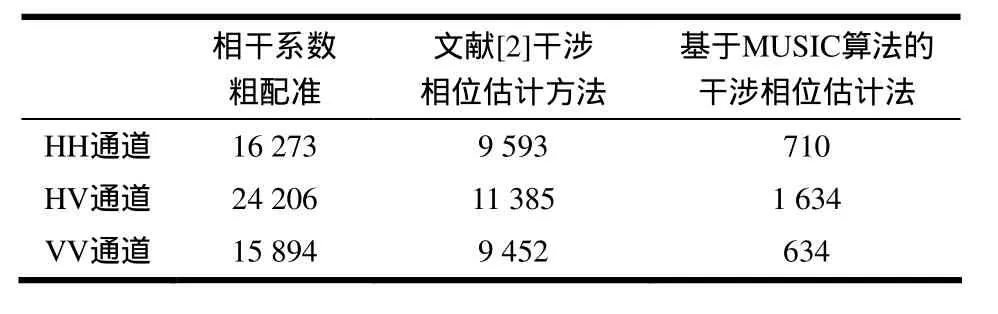
表1 各极化通道干涉相位图残差点数统计

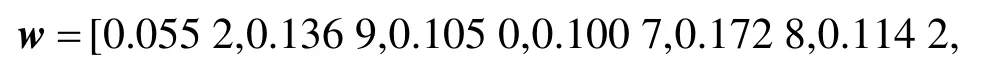
另外，文献[2]中的最优权值w的搜索过程还大大增加了计算量。假设SAR图像大小为M×N，从相邻像素中获取独立同分布的样本数为L，则在图像精配准过程中，文献[2]方法所需加法次数为12(L−1)MN，乘法次数为12(L+1)MN；本文方法所需加法次数为3(L−1)MN，乘法次数为(3(L+1)+1) ×MN。该方法由于避免了w的搜索过程，大大降低了计算量。同时，由于利用了MUSIC算法，极大地抑制了相位噪声，提高了干涉图的质量。

传统方法以一个极化通道SAR图像的配准误差对其他极化通道图像作配准处理是不准确的，而本文方法估计了不同极化通道的最佳滤波器参量，即各极化通道的配准误差不一样，从而可准确得到各极化通道的干涉相位图。通过该方法准确地估计出了多极化干涉相位，提高了极化干涉SAR不同极化组合干涉相位的精度，为极化干涉SAR复杂场景地形地表参数精确反演提供了基础。

4 结 论

结合空间谱估计理论，本文提出了基于MUSIC算法的Pol-InSAR多极化干涉相位估计方法。该方法通过维纳滤波理论得到各极化通道的最佳滤波器参量，构造多极化干涉信号模型，利用包含干涉相位的信号子空间与噪声子空间的正交性，准确地估计出多极化干涉相位。同时该方法具有自适应图像配准功能和很强的噪声抑制能力。与文献[2]相比，本文方法得到的图像配准精度更高，并且降低了计算量。实测数据证明了该方法的正确性和有效性。

[1] 吴一戎, 洪文, 王彦平. 极化干涉SAR的研究现状和启示[J]. 电子信息学报, 2007, 29(5): 1258-1262.WU Yi-rong, HONG Wen, WANG Yan-ping. The current status and implications of polarimetric SAR interferometry[J]. Journal of Electronics & Information Technology, 2007, 29(5): 1258-1262.

[2] 李海, 廖桂生. InSAR自适应图像配准的干涉相位估计方法[J]. 电子学报, 2007, 3(35): 420-425.LI Hai, LIAO Gui-sheng. An estimation method for InSAR interferometric phase with adaptive image coregisreation [J].ACTA Electronica Sinica, 2007, 3(35): 420-425.

[3] 龚耀寰. 自适应滤波[M]. 2版. 北京: 电子工业出版社,2003.GONG Yao-huan. Adaptive-filtering[M]. 2nd ed. Beijing:Publishing House of Electronics Industry, 2003.

[4] 何子述, 夏威. 现代数字信号处理及其应用[M]. 北京:清华大学出版社, 2009.HE Zi-shu, XIA Wei. Modern digital signal processing and using[M]. Beijing: Tsinghua University Press, 2009.

[5] 皮亦鸣, 杨建宇, 付毓生, 等. 合成孔径雷达成像原理[M]. 成都: 电子科技大学出版社, 2007.PI Yi-ming, YANG Jian-yu, FU Yu-sheng, et al.The imaging theory of Synthetic Aperture Radar[M]. Chengdu:University of Electronic Science and Technology Press,2007.

[6] ROSEN P A, HENSLEY S, JOUGHIN I R, et al. Synthetic aperture radar interferometry[J]. Proceeding of the IEEE,2000, 88(3): 333-382.

[7] BAMLER R, HARTL P. Synthetic aperture radar interferometry[J]. Inverse Problem, 1998, 14: 1-54.

[8] EICHEL P H, GHIGLIA D C. Spotlight SAR interferometry for terrain elevation mapping and interferometric change detection[R]. [S.l.]: Sandia National Labs Tech Report,1993.

[9] LANARI R, FORNARO G. Generation of digital elevation models by using SIR-C/X-SAR multifrequency two-pass interferometry: the etna case study[J]. IEEE Trans on GRS,1996, 34(5): 1097-1114.

[10] LEE J S, PATHANASSIOU K P. A new technique for nosie filtering of SAR interferometric phase images[J]. IEEE Trans on GRS, 1998, 36(5): 1456-1465.

[11] LOMBARDINI F, MONTANARI M, GINI F. Reflectivity estimation for multibaseline interferometric radar imaging of layover extended sources[J]. IEEE Trans on Signal Processing, 2003, 51(6): 1508-1519.

[12] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M].北京: 清华大学出版社, 2004.WANG Yong-liang, CHEN Hui, PENG Ying-ning, et al.Space spectrum estimation theory and algorithm[M].Beijing: Tsinghua University Press, 2004.

[13] 王超, 张红, 刘智. 星载合成孔径雷达干涉测量[M]. 北京: 科学出版社, 2002.WANG Chao, ZHANG Hong, LIU Zhi. The satellite synthetic sperture radar interferometry[M]. Beijing:Science Press, 2002.