用递归BDD技术分析故障树
2011-04-26王厚军黄建国
罗 航,王厚军,黄建国,龙 兵
(1. 四川大学测量控制系 成都 610065; 2. 电子科技大学自动化工程学院 成都 611731)
故障树分析(fault tree analysis, FTA)方法在宇航、核能、电子电力系统等领域中已成为评价可靠性和安全性的重要手段[1-5]。早期的Fussell-Vesely算法[6]和Semanderes算法[7]都可以采用布尔吸收策略来得到顶事件的最小割集(minimum cut set, MCS),这在故障树定性分析方面是可行和有效的。然而,要对故障树进行定量分析,则必须首先对顶事件的MCS进行不交化处理。但是,对MCS进行不交化处理的容斥定理是一个“NP”困难问题[2],其主要原因是不同割集中的相同底事件(这样的割集不能被吸收)在顶事件的交并运算中可能导致运算量剧烈增加,即所谓“组合爆炸”问题。虽然直接[8]或早期不交化[9]故障树结构函数在一定程度上可以减少运算量,但是采用不交型积之和定理[10]实现割集不交运算的过程是烦琐和费时的。
二元决策图(BDD)技术最早用于数字电路的简化分析和结构设计。作为一种新兴的分析工具,BDD技术已广泛应用于可靠性分析及故障诊断领域。其重要作用在于能直接显示顶事件故障形成的逻辑路径;直观显示系统故障(顶事件)的薄弱环节。本文用BDD技术快速实现故障树的定性分析,讨论BDD技术的相关理论,研究并实现其关键算法。进行这些研究的主要原因在于:1) 基于Shannon分解定理的BDD技术能够直接实现故障树结构函数(本质为最小割集的并集形式)的不交化分解[11-13],而这种分析过程可以同时得到故障树的MCS。显然,这比联合运用Fussell-Vesely算法(或Semanderes算法)和不交化原理(以下简称联合方法)进行故障树分析更方便直接。2) BDD技术是建立在一定理论基础上的,需要研究其连接规则。为了获得故障树顶事件的BDD结构,需要分析具体的实现方法——递归方法。3)用BDD技术获取故障树的不交化割集,涉及路径搜索。本文提出一种继承父节点信息的递归方法来快速实现不交化,需要深入讨论并分析其实现过程。
1 BDD的故障树原理及其实现规则
Shannon分解使得影响顶事件故障(正常)状态的基本事件及传播路径变得清晰有序,而BDD技术则是实现和简化Shannon分解的有效工具。
1.1 故障树结构函数的Shannon分解

1.2 基于BDD技术的故障树分析原理
BDD技术拓展了Shannon分解的功能,使故障树结构函数的产生与割集不交化同时实现成为可能。BDD技术是一系列原理、方法及实现的有机整体。三元逻辑运算符ite(if-then-else)是分析全过程的有力工具。
1.2.1 ite运算符及其在逻辑运算中的应用
故障树底事件间的关系从属于逻辑门的性质,为了用一种方式统一描述底事件自身及其相互间的关系,定义ite运算符[14]为:
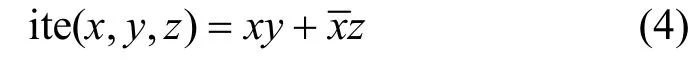

图1 ite(x, y, z)的二叉结构形式
ite结构可以描述以下3种重要关系:

ite运算符为进一步分析事件和结构函数的关系奠定了同源描述的基础,也使全面分析故障树成为可能。
1.2.2 基于ite运算符的BDD连接规则

式中,i1,i2,L,in是{1,2,L,n}的一个排列,且i1, 显然,式(9)是具有ite形式的层次结构。如果知道了形如式(9)的两个BDD结构形式M和N,需要用ite运算符来连接它们。因为如果能够得到连接两个BDD结构的ite操作形式,再用递归方式,将很快得到整个故障树的BDD。下面分析这种连接过程。 2) 两个重要的连接规则。 事实上,M和N一定是通过某种逻辑操作而联系起来的。考虑到经过规范化处理的故障树只含有“或”或“与”逻辑门及底事件,则分析M〈op〉N的ite连接关系时,op表示逻辑“或”(用“+”表示)或“与”操作。 假设两个子BDD结构分别为: 将xi和xj作比较,两者指标(下标)只有相等或不等。当不等时,可以选择最小根节点(指标最小的节点)作为标准。因此,操作规则实质上只有两种。 综合情况1和情况2,式(13)得证。 式(12)和式(13)是形成故障树BDD的关键规则。虽然它们是为连接两个子BDD结构而发展的,但其连接对象并不局限于子BDD结构,事实上,它们连接的对象可以是两个基本事件。 基于BDD技术的故障树分析能够同时实现MCS及其不交化过程,但其实现要分两个步骤:1) 形成顶事件的BDD结构;2) 在获得的BDD结构基础上得到割集的不交化形式。 故障树结构输入表描述了基本事件及逻辑门间的关系。BDD结构的递归实现也正是从结构输入表的逻辑门开始的。其步骤如下: 1) 建立两个n行1列的元胞数组FTS和BDS(n表示故障树中逻辑门的个数)。FTS存储不同逻辑门的输入元素,BDS存储各逻辑门的BDD结构。置i=n。 2) 根据门i的类型,利用ite运算符连接FTS{i}中的底事件;连接后的结果A保存在BDS{i}中,即BDS{i}=A。 3) 置i=i−1,如果门i−1的输入中仅有底事件,则重复步骤2)。 否则,如果输入是底事件和输入逻辑门的混合情况(第i−1个逻辑门的输入中,一部分是底事件,另一部分是另外的逻辑门),则重复步骤2)的前半部分,即得到的结果置为A;计算输入逻辑门的个数m,置j=1,A=BDD_ITE_CAL(A,G(j),TYPE);置j=j+1,重复A=BDD_ITE_CAL(A,G(j),TYPE),直到j=m。 如果输入全为逻辑门,则置第一个逻辑门的BDD结果为A,其余步骤同输入是部分逻辑门的情况,置BDS{i}=A。 4) 重复步骤3),直到i=1,则BDS{1}为顶事件TBDD的BDD结构,即TBDD= BDS{1}。 其中,A=BDD_ITE_CAL(A,G(j),TYPE)是连接两个子BDD结构的函数,它是递归实现顶事件BDD结构的核心函数。简言之,该递归函数的输入参数A是一个子BDD结构,它与某子BDD结构中G(j)通过类型TYPE连接后,输出新的子BDD结构A,为进一步连接新的子BDD创造了递归基础。G(j)代表某个逻辑门的输入元素BDS{k},是子BDD结构。 顶事件BDD结构的实现精确地描述了底事件对顶事件影响的状态及路径。本质上讲,这种状态和路径的表述就是顶事件的不交化割集。实现顶事件BDD结构的不交化割集的方式是路径搜索,当某条路径搜索完毕,该路径上的节点以某种方式排列成的链就形成一个不交割集(相对其他割集而言)。不交割集链形成的关键在于继承操作。 在搜索过程中,每个中间节点都直接继承它的父节点所继承的全部信息,且以特定方式继承父节点的信息。当父节点向左分支(分支边标定“1”)到达子节点时,子节点直接继承父节点的信息;当父节点向右分支(分支边标定“0”)到达子节点时,子节点继承的是父节点的补信息。 继承关系是不交化割集形成的一个重要环节。在继承的作用下,不交化割集的路径不断形成(通过不断分支以深度优先方式进行搜索)。由于路径在叶节点值为“1”的位置结束,所以BDD结构中叶节点值为“1”的个数就是不交化割集的数目(虽然在搜索前不一定知道这个数目)。每个不交化割集由某节点(其左分支的值为“1”的叶节点)和它的继承信息共同形成(通过“与”关系)。分析顶事件的BDD结构[15],如图2所示,显然该结构有4个不交化割集。 图2 某仿真故障树的BDD结构 在继承操作下,不交化割集的形成具有重复性很高的规律,因此其搜索过程在本质上也是递归的。 为了说明用BDD分析故障树的优势,下面以一个具体的例子[17]加以说明。 故障树结构如图3所示,表1是对应的故障树结构输入表。 运用BDD技术,得到顶事件(门1的输出)的BDD结构为: 根据编程设置,式(14)实际上是一个含有3个元素嵌套的元胞数组,其直观结构如图4所示。表2列出了基于BDD结构的不交化割集及析出的MCS。 图3 故障树结构 如前所述,利用联合方法得到不交化割集的过程是烦琐的,而利用BDD技术则可直接得到不交化割集。为了比较两者之间的效率,表3列出了两种方法的运行时间(CPU为AMD Sempron(tr) Processor 3000+,1.61 GHz主频,内存为512 MB)。 表1 故障树的结构表 图4 故障树的BDD结构 表2 故障树的不交化割集(割集) 表3 形成不交化割集的运行时间 单位:s 与传统的Fussell-Vesely(F-V)算法及不交化积之和定理相比,基于BDD技术的故障树分析具有明显的优势。 首先,BDD技术比联合方法的功能更完善。BDD技术将实现结构函数和不交化过程统一起来,一次性实现两方面的要求,直接实现表2中的不交化割集(已经通过化简处理),其最小割集很容易从不交割集中析出(只需将不交割集中的补事件去掉)。而联合方法中的F-V算法只能得到顶事件的割集,割集的不交化处理只能在最小割集的基础上运用过程繁复的不交型积之和定理来实现。简言之, BDD技术实现:不交化割集处理→割集;而后两者联合实现:割集→不交割集处理。故障树定量分析的必要条件正是得到不交化割集及其简化处理形式。从该意义上讲,BDD技术比另外两者联合运用的功能更完善。 最后,用BDD技术获得不交化割集的思想比用后两者联合处理得到不交化割集简单。用BDD技术获得不交型割集的过程仅涉及函数的递归调用,处理的对象是事件本身,采用的方式是继承事件的信息,在递归调用和继承的作用下,不交型割集的简化形式可以直接得到;联合方法中的不交化积之和方法处理的对象首先是割集,是在割集与割集之间进行比较和吸收,这种比较和吸收过程不但要遍历所有割集对(组合),还要遍历割集间的元素对(组合)。只有完成了这些遍历,不交化割集的简化形式才得以实现。 BDD技术是故障树分析的一种有效技术。在与传统故障树分析方法作比较的基础上,本文详细分析了BDD技术的原理、方法和实现过程。继承技术的运用是实现割集不交化的关键技术,本文对继承的方法和原因作了详细分析,并在具体的例证中验证了BDD技术优于传统故障树分析的原因。 [1] 李建平, 余建星. 模糊故障树分析方法在工程质量风险分析中的应用[J]. 水利水电技术, 2008, 39(2): 45-49.LI Jian-ping, YU Jian-xing. Application of fuzzy fault tree analysis to risk analysis of construction quality[J]. Water Resources and Hydropower Technology, 2008, 39(2): 45-49. [2] 王少萍. 工程可靠性[M]. 北京: 北京航空航天大学出版社, 2000.WANG Shao-ping. Reliability engineering[M]. Beijing:Beijing University of Aeronautics and Astronautics Press,2000. [3] KRASICH M. Use of fault tree analysis for evaluation of system-reliability improvements in design phase[C]//Proceedings of the Annual Reliability and Maintainability Symposium (S0149-144X). [S.l.]: IEEE, 2000: 1-7. [4] ARCIDIACONO G. Reliability improvement of a diesel engine using the FMETA approach[J]. Quality and Reliability Engineering International (S0748-8017), 2004,20(2): 143-154. [5] 宋保维, 毛昭勇, 王雯琴, 等. 基于故障树分析的鱼雷可靠性评定方法[J]. 系统仿真学报, 2007, 19(10):2180-2182.SONG Bao-wei, MAO Zhao-yong, WANG Wen-qin, et al.Reliability evaluation method of torpedo based on FTA[J].Journal of System Simulation, 2007, 19(10): 2180-2182. [6] FUSSELL J B, VESELY W E. A new methodology for obtaining cut sets[J]. Trans Am Nucl Soc Trans, 1972, 15(1):262-263. [7] SEMANDERES S N. A computer program for the efficient logic reduction analysis of fault trees[J]. IEEE Trans Nuclear Science, 1971, 10: 481-487. [8] 金星, 武江涛, 洪延姬. 一种新的故障树定量分析优化方法[J]. 中国空间科学技术, 2001, 21(3): 60-64.JIN Xing, WU Jiang-tao, HONG Yan-ji. A new optimized method for quantitative analysis of fault tree[J]. Chinese Space Science and Technology, 2001, 21(3): 60-64. [9] 刘永宾, 陈金水, 谢学武. 割集矩阵在早期不交化FTA中的应用[J]. 天津大学学报, 2000, 33(3): 318-323.LIU Yong-bin, CHEN Jin-shui, XIE Xue-wu. Study on the application of cut sets matrix to fault tree system analysis[J].Journal of Tianjin University, 2000, 33(3): 318-323. [10] 梅启智, 廖炯生, 孙惠中. 系统可靠性工程基础[M]. 北京: 科学出版社, 1987.MEI Qi-zhi,LIAO Jiong-sheng, SUN Hui-zhong.Foundation of system reliability engineering[M]. Beijing:Science Press, 1987. [11] 卢世荣, 方逵, 周经纶. BDD表示下的部件重要度的计算[J]. 系统工程与电子技术, 1999, 21(3): 70-74.LU Shi-rong, FANG Kui , ZHOU Jing-lun. The computation of importance of elements in fault trees presented by BDD[J]. Systems Engineering and Electronics, 1999, 21(3): 70-74. [12] 孙毅彪. 基于BDD故障树分析的海关风险识别理论及其应用[J]. 运筹与管理, 2008, 17(2): 501-505.SUN Yi-biao. A theory and Its application of binary decision dagrams based fault tree analysis in customs risk identification[J]. Operations Research and Management Science, 2008, 17(2): 501-505. [13] AKERS S B. Binary decision diagrams[J]. IEEE Transaction on Computer, 1978, 27: 509-516. [14] RAUZY A. New algorithm for fault tree analysis[J].Reliability Engineering and System Safety, 1993, 40(2):203-211. [15] 袁静, 胡昌华, 徐瑞, 等. 基于改进BDD算法的导弹安控系统故障树仿真分析[J]. 系统仿真学报, 2007, 19(1):10-11.YUAN Jing, HU Chang-hua, XU Rui, et al. Fault tree simulation analysis of missile safety control system based on improved BDD algorithm[J]. Journal of System Simulation, 2007, 19(1): 10-11. [16] 王红梅, 胡明, 王涛. 数据结构(C++版)[M]. 北京: 清华大学出版社, 2005.WANG Hong-mei, HU Ming, WANG Tao. Data structure(C++ version)[M]. Beijing: Tsinghua University Press,2005. [17] 张超. 基于BDD的动态故障树优化分析研究[D]. 西安:西北工业大学, 2004.ZHANG Chao. Optimization analysis of the dynamic fault tree based on BDD[D]. Xi’an: Northwestern Polytechnical University, 2004.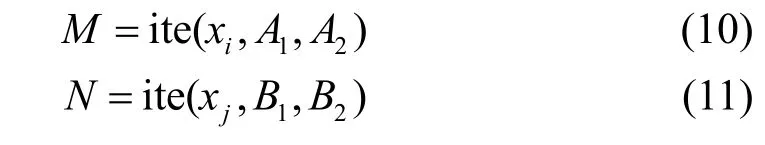

2 故障树BDD分析的递归实现
2.1 顶事件BDD结构的递归实现
2.2 BDD结构不交化割集的实现——继承操作


3 基于BDD的故障树分析的例子
3.1 基于BDD技术的运行结果

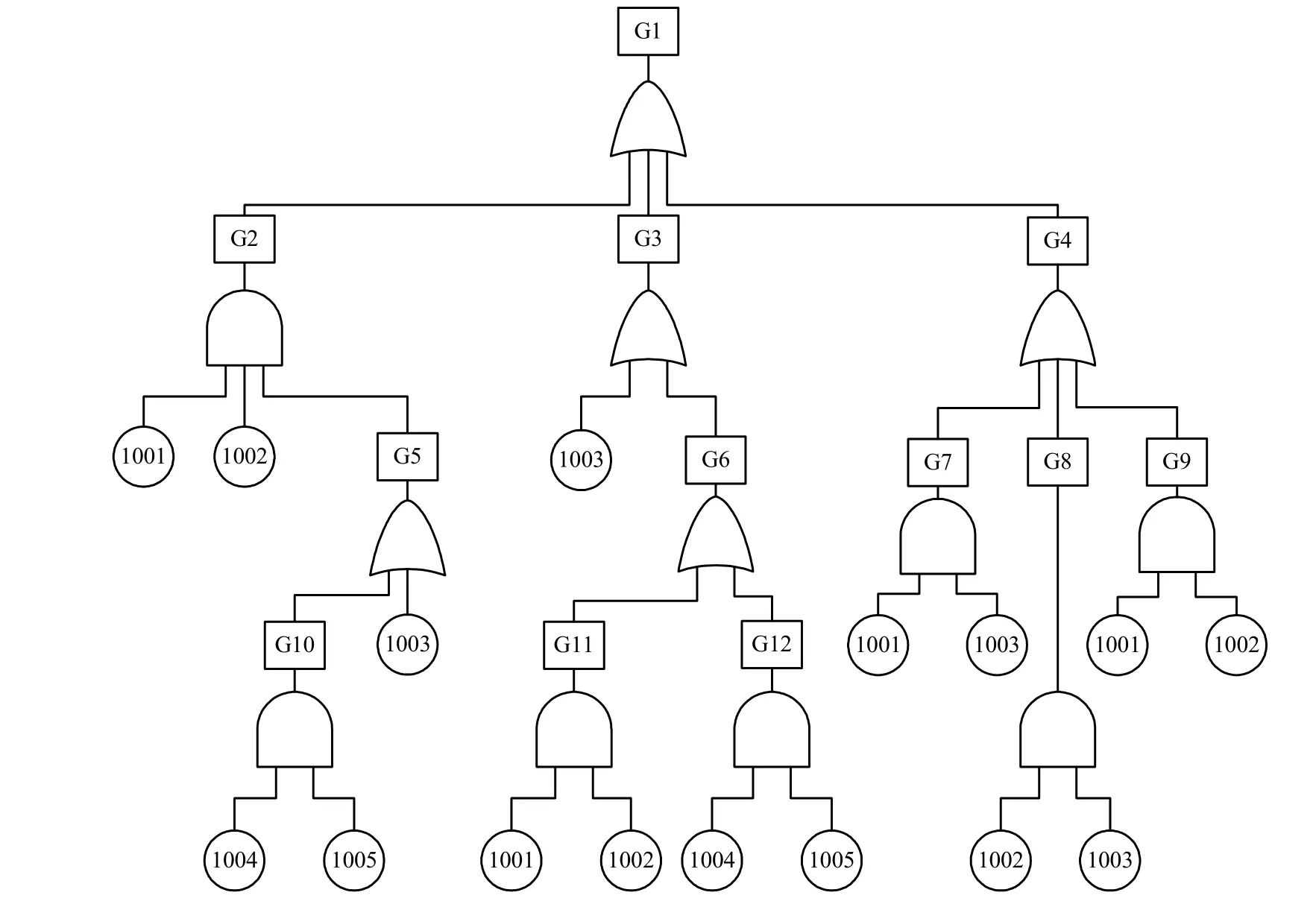




3.2 分析与结论

4 结 束 语
