基于扭杆摆的汽车动力总成惯量参数测量实现
2011-04-26查佳韵程金华程长洪
查佳韵,刘 勇,程金华,程长洪
(东风汽车集团股份有限公司技术中心,湖北 襄樊 441004)
0 引 言
现在常用三线摆法或复摆法测量汽车动力总成的惯量参数。根据三线摆或复摆的测量原理,动力总成各种姿态下的质心必须通过摆的转轴(或者添加配重块使动力总成质心通过摆的转轴),由于测试姿态较多,动力总成质量较大,加之其外形也不规则,因此使得测试工作变得繁琐耗时,且测量精度较低。同时,三线摆或是复摆的高度较高,占地面积较大,结构比较松散,给操作上也带来诸多不便[1-3]。
为提高测试的效率与精度,研发了一种基于扭杆摆的惯量测试设备。该设备结构紧凑,操作方便,能在1台设备上实现对汽车动力总成的质量、质心位置、转动惯量和惯性积等参数的测量,而且动力总成各种姿态可任意放置,无需调整,得到的测量结果具有较高精度。
1 惯量测试系统组成
测量系统结构示意图如图1所示,主要由扭杆、轴承、升降装置、称重平台、称重探头、光电传感器、摆动平台、底座以及称重传感器等组成。测量系统有称重状态与摆动状态两个工作状态。称重状态时,升降装置顶起称重平台,称重探头伸出与称重传感器接触,然后升降装置降下与称重平台脱离接触,此时称重平台、摆动平台及动力总成的重量全部落在3套称重传感器上,从而获得动力总成质量及总成偏离转轴中心距离;摆动状态时,升降装置顶起称重平台,退回称重探头,然后升降装置降下,使称重平台落在底座上,自摆动平台给予扭杆激励,带动动力总成摆动,由周期测量装置测量摆动周期。
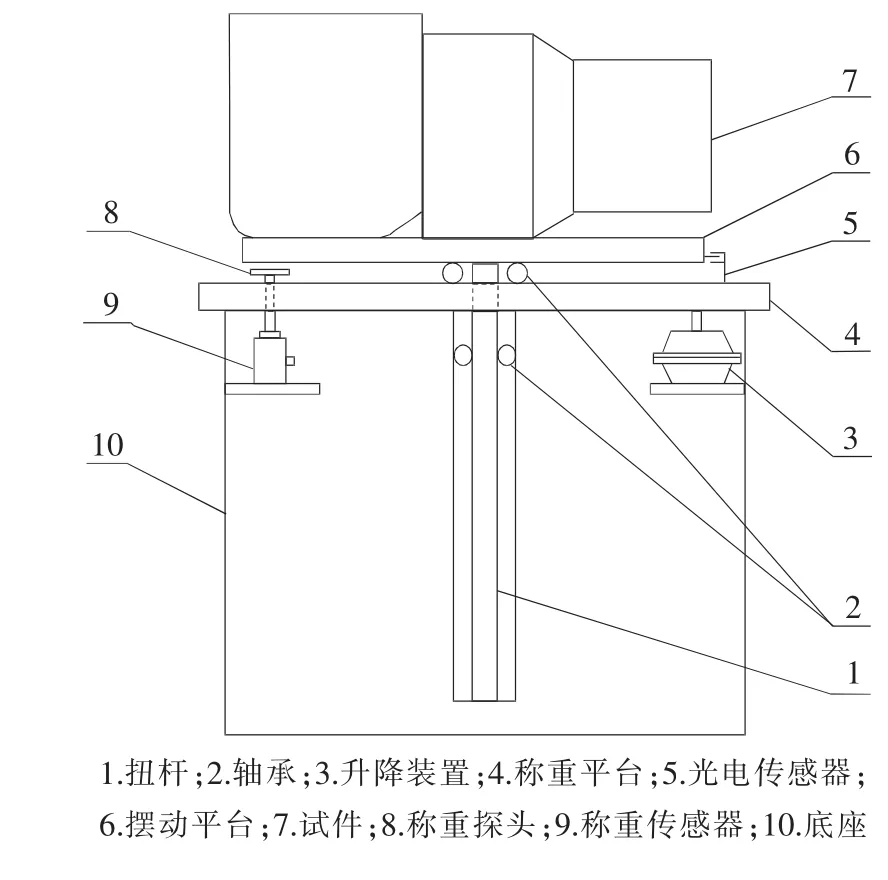
图1 转动惯量测试装置示意图
2 系统原理
2.1 转动惯量参数测量原理[4-5]
转动惯量可通过测量扭摆系统的自由摆动周期来计算。若不考虑系统阻尼,则

式中:I——试件及测试平台对转轴OH的转动惯量,kg·m2;
K——扭杆刚度系数,N·m/rad;
T——扭杆摆系统自由摆动周期,s。
其中,K可以通过对标准件的标定计算得到。因此,只要测量出扭杆摆的摆动周期T,就可以计算扭杆摆及发动机总成组合绕扭杆摆轴的转动惯量I为

若动力总成的质心通过转轴OH(见图2),则动力总成绕OH轴的转动惯量为
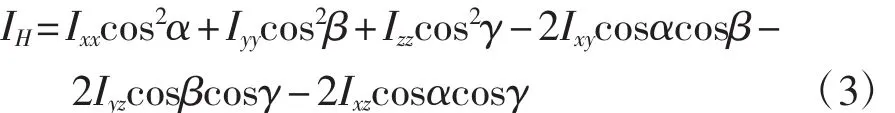
式中:IH——动力总成过其质心的转动惯量;
α,β,γ——旋转轴OH与动力总成坐标轴Ox,Oy,Oz的夹角;
Ixx,Iyy,Izz和Ixy,Iyz,Ixz——动力总成绕其坐标轴的3个惯量矩和3个惯性积。
由IH的计算式可知,要得到惯性张量的全部6个值,至少需要测量总成6种不同状态的转动惯量,一般则测试10~12个姿态的数据进行拟合计算,以提高测试结果精度。
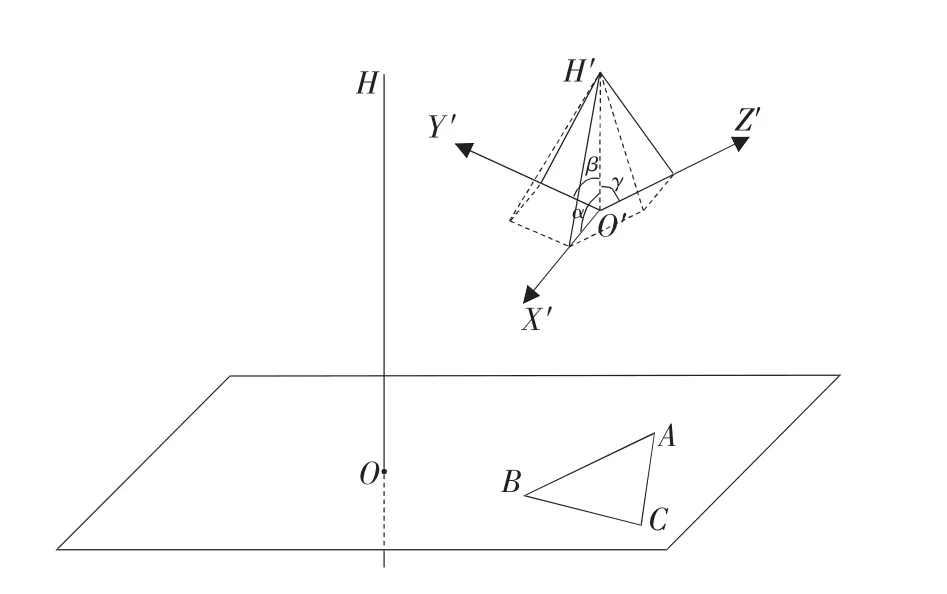
图2 汽车动力总成坐标系O′X′Y′Z′与测试台转轴OH的夹角α β γ示意图
通过扭杆摆系统测得的转动惯量I不但包括发动机总成的转动惯量,还包括扭杆摆系统自身的转动惯量。通过式(4),得到过发动机总成质心绕扭杆摆转轴的转动惯量IH为

其中:I——扭杆摆系统及总成转动惯量测量值;
I0——扭杆摆的转动惯量,也称皮转动惯量;
m——发动机总成的质量;
Rm——发动机总成质心的投影到转轴OH的距离。
于是有

2.2 空间姿态角的测取
为了测量发动机总成坐标系各轴与扭杆摆转轴之间的空间夹角α,β,γ,需要依靠总成的数模或者借助三坐标仪。
首先建立总成试件的坐标系(只在首个姿态建立坐标系),在总成试件上确定至少3个特征点(为了可以让总成试件任意放置各种姿态后都可以方便测量,最好多找一些点),给出这些特征点相对于总成试件坐标系的坐标,比如特征点D1(XD1,YD1,ZD1),D2(XD2,YD2,ZD2)等,另外在测量平台上也确定3个特征点A,B,C。然后用三坐标仪测量试件上的特征点到平台上的点的距离,便可以得到一个三元二次非线性方程组,利用Matlab编程求解这个方程组可以将平台上的点相对于发动机坐标求出,进而得到α,β,γ。
在图2中,平移转轴OH至试件坐标系中O′H′位置,α,β,γ 分别为试件坐标 OX′、OY′、OZ′与转轴O′H′的夹角,则单位向量 O′H′在试件坐标系 O′X′Y′Z′中可以表示为(cosα,cosβ,cosγ)。由于单位向量 O′H′垂直于平面ABC,于是有
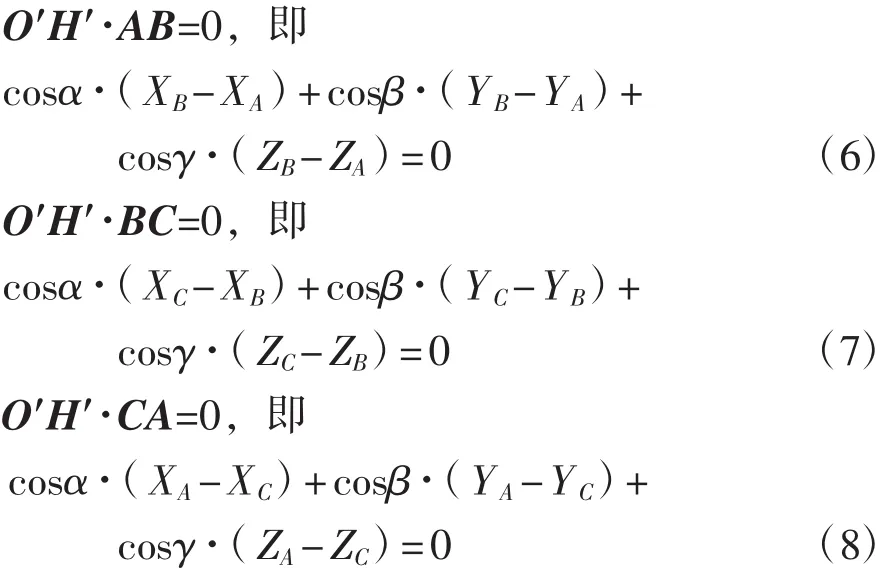
联立式(6),式(7),式(8)求解,即可求得 cosα,cosβ,cosγ。
2.3 偏心距的测取
动力总成偏离扭杆摆转轴的距离利用称重测试平台完成[6]。称重平台包含3个圆周均布的称重传感器M1,M2,M3。建立称重测试平台坐标系如下:平台中心O与M1传感器中心的连线为测试平台坐标系的X轴,Z轴通过O且与测试平台平面垂直向上,测试平台坐标系符合右手定则,如图3所示。设总成质心投影在OXY平面内C点,则根据力平衡原理有

在平面OXY内对OX取矩可得总成试件在OXY平面内的y向质心yc为

在平面OXY内对OY取矩可得总成试件在OXY平面内的x向质心xc为
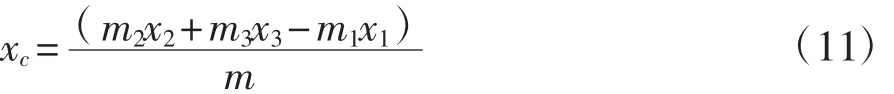
于是,总成试件质心投影在扭杆摆测试平台上偏离转动中心的距离ΔR为

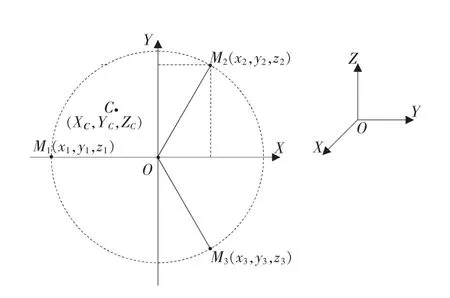
图3 测试平台坐标系
2.4 惯性主轴及方向余弦
在动力总成上建立曲轴坐标系OXYZ坐标系,O为发动机质心,X轴平行于发动机曲轴轴线,Z轴垂直向上,Y轴由右手定则确定。
动力总成坐标系中的惯性参数 Ixx,Iyy,Izz,Ixy,Iyz,Izx通过扭杆摆系统测试计算得到,按如下方法可以求出主惯性矩Ixp,Iyp,Izp及主惯性矩在动力总成坐标系中的方向余弦。构造惯性矩矩阵[S]为
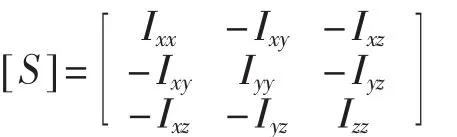
当惯性积 Ixy,Iyz,Izx分别为零时,矩阵[S]变为[S′],即
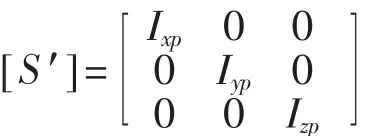
此时 Ixp,Iyp,Izp即为主轴惯性矩。对比[S]与[S′],求解[S]矩阵的标准特征值,所得到的3个特征值即为主惯性矩,特征值所对应的模态向量即为相应的主惯性轴的方向余弦。
2.5 方程组最小二乘法
对测试数据采用方程组最小二乘法进行拟合处理[7-9]。惯量参数由求解线性方程AX=I得到,其中有
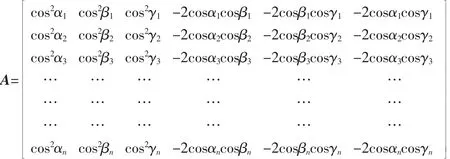
X=[IxxIxyIzzIxyIyzIxz]T为待求的惯性参数,亦称惯性张量;
I=[IH1IH2IH3… IHn]T为通过总成试件质心的不同轴的转动惯量。
假设产生 n(n≥6)次测量,即有

式(13)是一个超定方程。为进行方程求解,采用最小二乘法。在方程两边左乘ATn×6,则有

从而方程转化为

进而可解得n次测量的惯性张量X。为减小误差,可以利用求得的惯性张量值代入式(13)中与每次测量进行比较,然后剔除偏差大的测量值,之后重新进行最小二乘拟合,由此获得更好的测试结果。
3 误差分析
3.1 周期测量误差
周期测量采用光电传感器测量。设周期测量误差为ΔT,所造成的转动惯量测量相对误差为
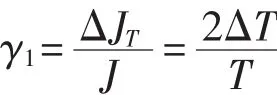
经测试,扭杆摆空摆周期1.734s,周期测量误差小于0.1ms,于是,转动惯量测量相对误差为
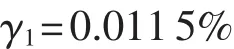
3.2 质心偏移误差
由于加工、装配以及称重传感器误差的原因,定位动力总成质心偏离扭杆摆转轴的距离R时会存在误差ΔR,依据平行轴定理,所造成的转动惯量测量相对误差为
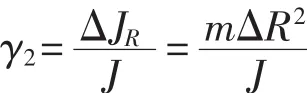
设最大定位误差ΔR=10mm,以某质量为200.4kg,转动惯量为3.461 5 kg·m2的标准件为例,相对误差为
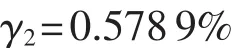
3.3 阻尼误差
采用的扭杆摆系统,存在机械摩擦、空气阻力以及扭杆变形等因素影响周期[10-11],使得系统形成有阻尼的振动,其振动方程为

求解方程有
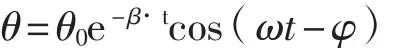
式中:θ——扭摆角;
β——与阻尼相关的系数;
综上所述,总误差为
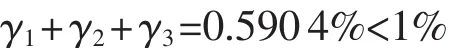
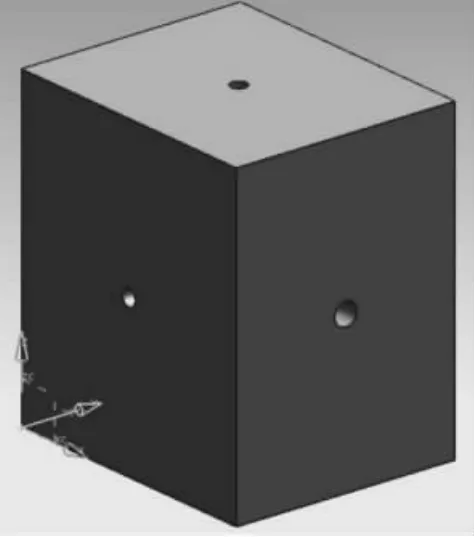
图4 方形标准块UG模型

图5 方形标准块标定
4 标准块实例
测量目的是要获得汽车动力总成的惯性矩与惯量积参数,这些参数是通过测试手段与程序计算获得的,因此需要对测试方法与相关的软件计算程序进行验证。现在利用一个方形标准块进行惯量参数计算程序的验证,然后将验证结果与标准块的数模进行对比,方形标准块的UG模型见图4,标定系统见图5。标定测试过程中,共改变方形块10个姿态,得到10组数据,拟合数据如表1。
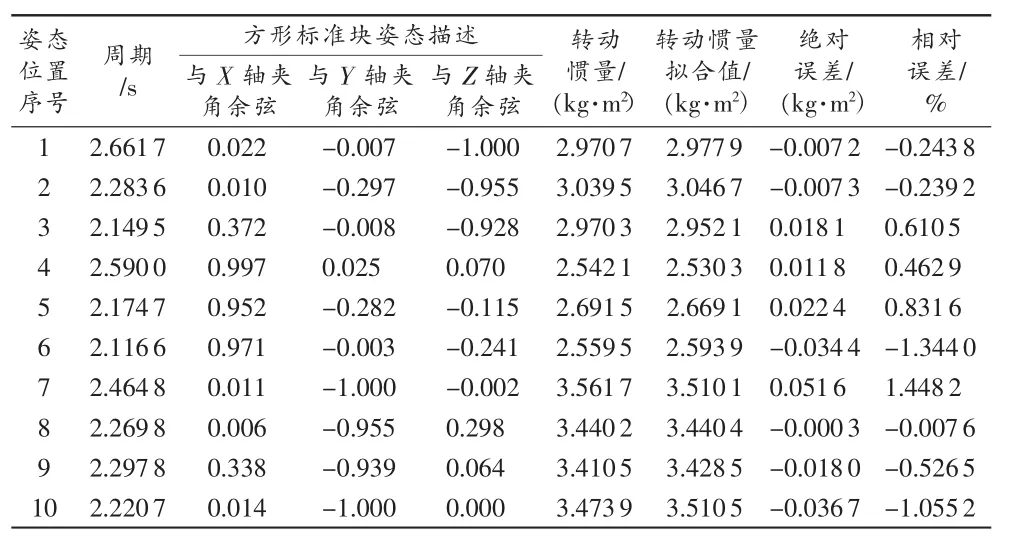
表1 标准块惯性矩惯性积测试数据(原始拟合)
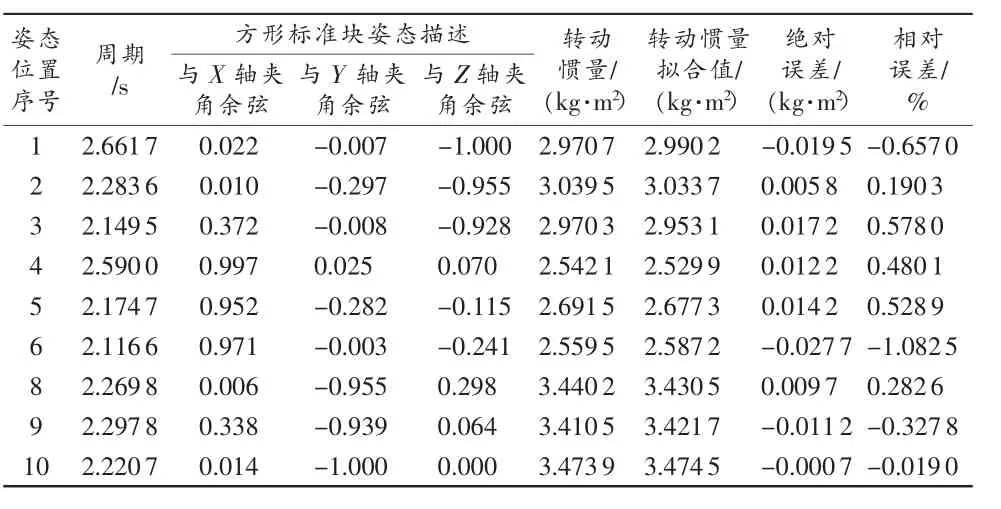
表2 标准块惯性矩惯性积测试数据(剔除拟合)
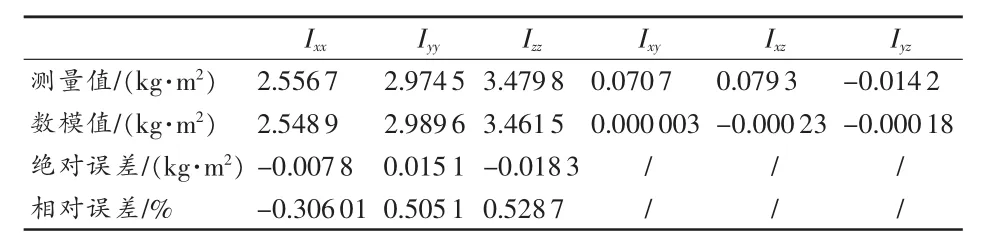
表3 标准块测试数据与数模值对比
表1中,第7组数据拟合偏差较大,剔除该组数据,重新拟合如表2。根据表2的数据计算得到方形标准块的惯性矩、惯性积参数,与方形标准块的UG数模值比较,如表3所示。从结果数据看,验证得到的数据结果与数模值吻合良好(由于标准方块的惯性积数值本身很小,在此不进行误差计算),说明测试方法与计算软件正确。
5 结束语
设计的基于扭杆摆的汽车动力总成惯量参数测量装置,克服了三线摆等测量方式操作繁琐耗时的缺点,可以将总成任意位置放置,操作简便,且惯量参数测试结果精度较高,具有较好的实用性。
[1] 刘振东,郑桂梅,孙兴川.基于扭摆法的转动惯量测量[J].河南科学,2008,26(10):1181-1185.
[2] 李惠彬,刘海光,刘吉春.发动机动力总成惯性参数的扭摆测试研究[J].计量与测试技术,2007,34(6):52-54.
[3]郭长立,李三庆.落体法测刚体转动惯量的测量方法比较[J].力学与实践,2005,27(3):69-72.
[4] 丁雪松,李慧鹏,王军,等.高精度转动惯量测量设备的研制[J].计量技术,2007(9):12-15.
[5]袁昌盛,宋笔锋.改进复摆法测量转动惯量的方法和设备研究[J].中国机械工程,2006,17(6):598-600.
[6] 吴斌,马贵贤,彭敏燕,等.卫星转动惯量测量方法的研究[J].宇航计测技术,2008,28(2):21-23.
[7] 吕振华,罗捷,范让林.汽车动力总成悬置系统隔振设计分析方法[J].中国机械工程,2003,14(3):265-269.
[8] 鲍晓东,侯勇.汽车动力总成悬置系统解耦设计研究[J].西安科技大学学报,2007,27(3):490-493.
[9]唐静.动力总成悬置系统在扭矩轴坐标系中的优化[J].西华大学学报:自然科学版,2010,29(3):20-24
[10]李彤华,朱占刚,尚春民,等.扭振法测弹体转动惯量的误差分析[J].长春理工大学学报:自然科学版,2007,30(3):63-66.
[11]唐应时,肖启瑞,李雪鹏,等.车辆复杂外形零部件转动惯量测量研究与误差分析[J].现代制造工程,2009(6):81-84.
