整体四柱式力传感器弹性体的有限元分析

2011-04-26陈世超徐尹杰

中国测试 2011年3期

易伟，陈世超，徐尹杰

（中国测试技术研究院，四川成都 610021）

0 引言

20世纪90年代初，全球知名的应变式传感器公司——美国STS公司开发出整体多柱应变式传感器，可用于测力、称重等领域，相比传统的单柱式传感器，抗偏载和抗横向载荷的能力显著增强[1]，目前已经有少数国内传感器厂家开始设计并生产此类传感器。但是由于设计方法和加工技术等方面的缺陷，国产此类传感器的性能水平还远低于同类进口产品。因此，有必要对该结构进行仔细的分析和探讨。近年来，有限元分析方法发展迅速，已经成为产品设计、性能研究等方面的必要手段，运用强大的有限元分析软件可以模拟各种复杂的工况，计算出结构的位移、应力、应变、热场分布等情况，极大地节约了设计开发的成本和时间。

1 整体四柱式力传感器弹性体结构的线性分析

1.1 力传感器线性的定义

直线性，又称为非线性，根据JB-T 7483-2005《半导体电阻应变式力传感器》[2]，定义为

式中：δL——非线性，%；

ΔU1max——各校准点在同一行程上的3次测量输出电压值的算术平均值与工作直线相应点的值之差的绝对值的最大值，mV；

UFS——额定输出电压值，mV。

此方法计算的非线性是力传感器性能一个重要考核指标，但不能直接使用于实际工作。因为在校准和检定过程中不可能无限连续施加负荷，往往只能在传感器量程10%～100%范围内取平均5～6个点去施加负荷[3]，获得相应的校准值。在使用的过程中不一定每次都是定点使用，量程内的任意插值点都落在误差范围内，这就要求传感器的线性好，并且在计量校准后也应提供对应的线性校准方程。

这样校准方程往往用多项式[4]式（2）来表示：

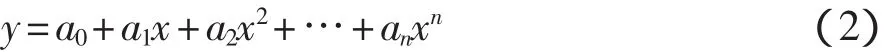
式中：a0——零点输出；

a1——传感器的灵敏度；

a2，a3，…，an——非线性参数。

多项式的次数取决于所需求的准确度，一般情况取3次就很精确[5]。

1.2 有限元模型的建立

运用三维CAD软件Solidworks进行整体四柱式力传感器弹性体的三维实体建模，该弹性体的设计量程为300kN，主要的结构参数如图1所示。选用大型有限元分析软件Algor进行分析[6]，Algor可以直接导入Solidworks格式的零件，实现模型数据的无缝转换，极大地简化了复杂的前处理过程。

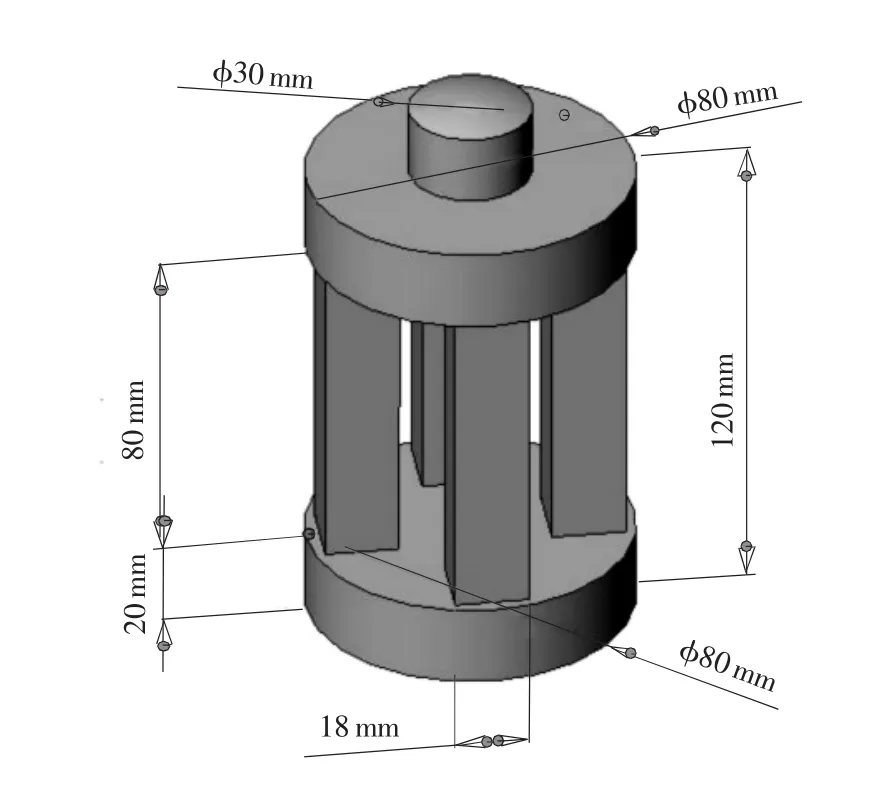
图1 三维模型及结构参数

力传感器弹性体材料多为合金钢和不锈钢，不锈钢传感器在传感器技术发达国家应用很普遍，我国由于材料生产、热处理工艺等技术的限制，应用很少，我国大力值传感器的技术水平较低。因此，设计材料选用沉淀硬化不锈钢17-4PH[7]，具有一定的前瞻现实意义。17-4PH的主要参数：弹性模量E=196 GPa，泊桑比为μ=0.272，密度为7.78×10-6kg/mm3。

因整体四柱式力传感器弹性体的结构对称，并不十分复杂，进行整体分析。以3mm绝对网格尺寸的划分网格，得到6508个单元，划分后的模型及坐标系如图2所示，在减小计算量、节省分析时间的同时，也能得到较好的分析结果。

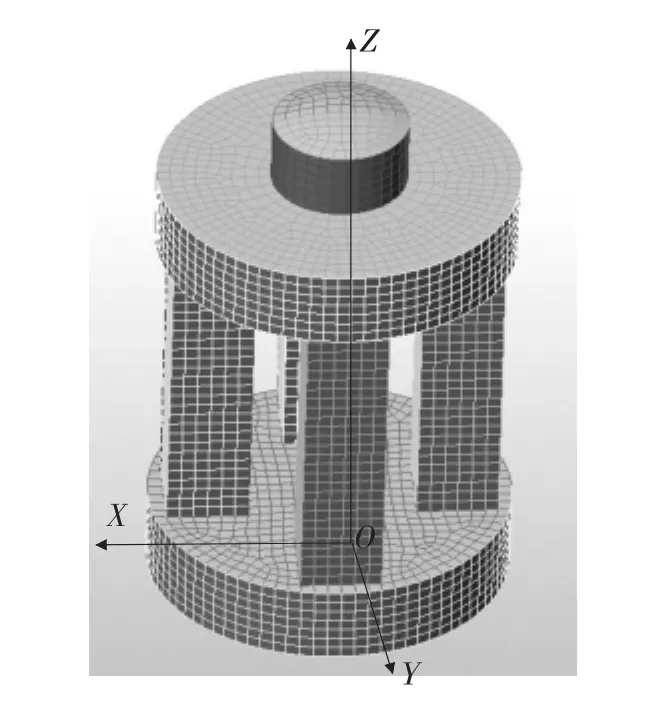
图2 有限元网格划分及坐标系

1.3 线性静力分析

按照力传感器日常的使用情况，设置弹性体底面的边界条件为固定（全约束），在压头球面上分别施加 30，100，200，300 kN 4 种工况的表面力负荷，力的方向为沿Z轴负方向。

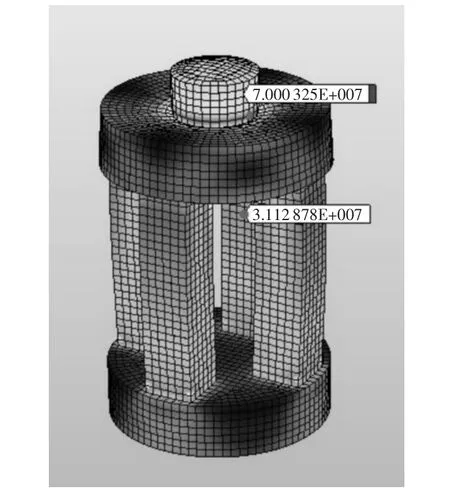
图3 30kN负荷下的应力分布图

工况1时，负荷为30kN，弹性体应力应变情况如图3。由图3可见，最大的应力为70MPa，集中在上压头与上平面的过度处；柱体内侧上半部分中间处应力较为集中，适合贴应变片[8-9]。由于弹性体结构对称，因此以四柱中任意一柱中位于该处的某一节点为参考，就可以考察应变片所受的应力应变。选节点编号为4223的节点，如图3所示，该处的von Mises应力值为31.129MPa。依次按工况2、3、4进行计算分析，可分别得到100，200，300kN负荷下，弹性体的应力、应变图。

满量程时，施加300 kN的负荷，压头与弹性体上平面过渡处产生最大应力为700 MPa（见图4）。17-4PH为高强度硬化不锈钢，不同的热处理工艺下屈服强度略有不同[10]，一般可达到1 000 MPa左右，压头产生最大位移为0.215mm，节点4223处产生的位移为0.081mm。由此可得出不同负荷情况下的弹性体4223节点的最大应变值，如表1所示。

图4 300kN负荷下的应力分布图

表1 不同负荷下节点4223的应变值

根据表1，可得弹性体受压时的线性方程为

将式（3）图形化得到图5，可见整体式四柱式力传感器弹性体的结构对称，受载均匀，线性相当好。

2 弹性体抗偏载能力的分析

设定偏心距e=5mm，即压头球面中心位置偏离Z轴5mm，载荷为300 kN，力的方向仍然设定沿Z轴负方向，其应力图见图6（应变图与此相同）。可见压头过渡处应力最为集中，达到1015.23 MPa，已达到或临近屈服点。为方便选取受载区域，必须对弹性体压头球面进行分割，并重新划分网格。因此1.3中的参考节点的编号有所改变，与1.3中4223节点相同位置的节点编号为4237，其他3柱相同位置的节点编号分别为3717、5277和4757，由此可获得偏载情况下4点的应变值，如表2所示。