可控硅调压系统中拼波角度求解算法的研究
2011-04-26胡洋洋程玉华
胡洋洋,程玉华
(电子科技大学自动化工程学院,四川 成都 611731)
0 引 言
可控硅拼波调压系统是以可控硅为控制对象,通过数字控制电路来完成电压(功率)调节的电器设备[1]。相比斩波调压方式,拼波调压方式能有效地抑制谐波分量,控制精度高,功率因数高,极大地改善了系统效率。该文以基于TI公司定点DSP芯片TMS320F2812的可控硅调压系统控制板作为实验平台[2-3],并结合系统中非线性方程的特点,使用IQmath库函数设计出相应基于二分法、弦截法和牛顿迭代法的算法[4],并通过实验对3种算法进行分析比较,最后确定牛顿迭代法作为系统中计算拼波角度的算法。
1 可控硅拼波调压原理
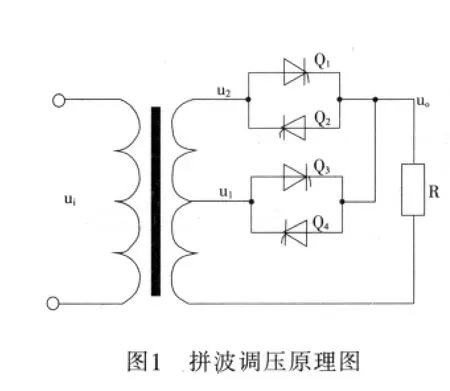
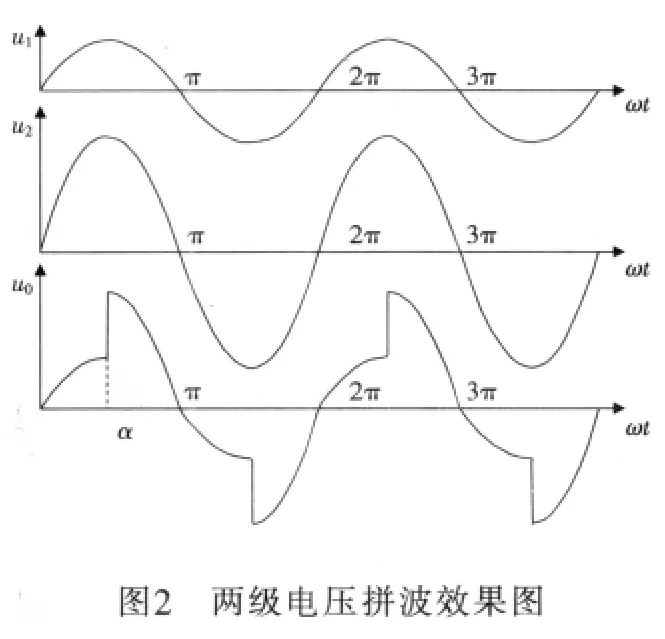
通过变压器副边2个抽头提供两级电压u1和u2,如图1所示,其中u2>u1,每个电压回路中的2个可控硅反向并联,用于控制本级电压的通断。以电压过零点作为可控硅触发时基,以正半周为例,首先触发Q3导通,此时由u1为负载提供电压,当导通角α时刻到来时,触发Q1导通,同时Q3因为反相电压而自动关断,u2为负载提供电压。负载上的拼波波形如图2所示。
在电压过零点后加入导通死区角度αD,以防止可控硅的共态导通,即在电压过零点后αD对应时刻小电压u1导通。那么可以得到负载电压有效值
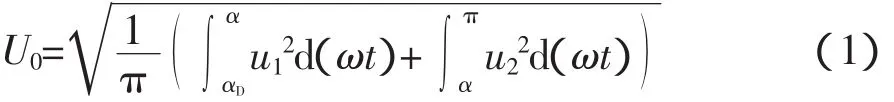
α∈[αD,π],其中 u1=U1sin(ωt),u2=U2sin(ω t),U1和U2为电压有效值,可以得到拼波角度α和负载电压有效值U0的方程为
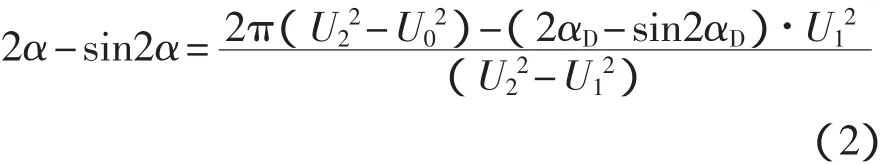
由于导通角α和负载有效电压值U0以及两级拼波电压有效值U1和U2存在定量的数值关系,需要找一种数值计算方法,由U0,U1,U2的值求解出导通角α。
令 x=2α, x∈[2αD,2π]
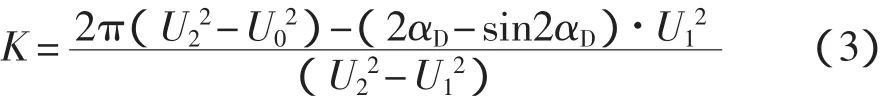
可得非线性方程

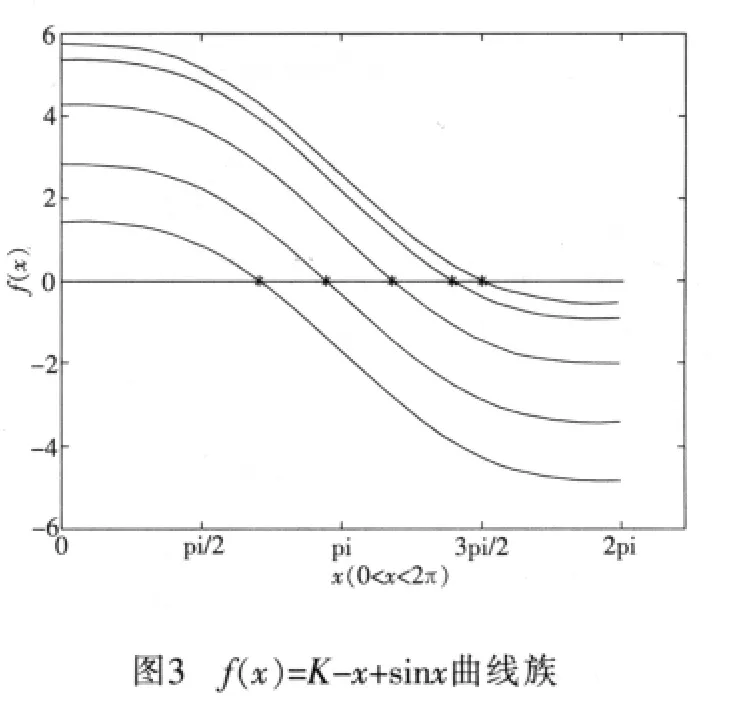
随机选取几个 U0,U1,U2的值后利用 Matlab对f(x)作图,可得式(4)的曲线族。如图3所示,随U0,U1,U2的变化,可得到不同的 f(x)曲线,可以看到方程f(x)=0有唯一解(图中星号标记处),并且曲线单调递减。
需要根据变压器抽头的U1、U2和用户设定电压U0,设计出基于DSP的求解f(x)=K-x+sinx的算法,并对算法进行比较验证。
2 求解非线性方程算法
2.1 二分法及相应算法
若f是区间[a,b]上的连续函数,且f(a)·f(b)<0,则f在[a,b]内必有1个零点。
由图3曲线族可知在确定的1组U0,U1,U2下,f(x)=0有唯一解,而且f′(x)=cosx-1<0,x∈[2αD,2π]。曲线f(x)单调递减,即可以通过式(4)确定导通角α的值。
根据F2812 DSP和系统的非线性方程的特点,对二分法求解作如下处理:
(1)从图3非线性曲线族可知,方程单调递减,所以在判断方程根的区间时,可由中值的符号来判断。例如若f(c)<0,则可判定f(x)在[a,c]内有根;若f(c)>0,则判定f(x)在[c,b]内有根。减少复杂的三角函数乘法,可大大提高代码的效率。
(2)以 c=a+(b-a)/2 代替 c=(a+b)/2 计算中点 c。这是为了坚持数值计算中通用策略,即通过把1个小的修正项加到先前的近似值来计算1个量是最佳的。
假设可控硅调压系统中导通角允许误差为0.1°,由(180/0.1)=1 800<211=2 048,所以可以知运算最大步数可设为n=11。软件具体实现的流程图如图4所示。
2.2 牛顿迭代法及相应算法
牛顿迭代法是利用泰勒级数的前几项去逼近求解实函数的零点,用某个固定公式反复校正根的近似值,使之逐步精确化,最后得到满足精度要求的结果。
唯一性证明:从图3的曲线族上可以看到方程f(x)=0有唯一解(图中星号标记处),即通过式(4)可以唯一确定α的值[5]。
算法求解的收敛性验证:
在经过i+1次迭代计算后[6],牛顿迭代公式误差由式(5)得到

式中:ei+1和ei——第i+1次和第i次计算后的误差。

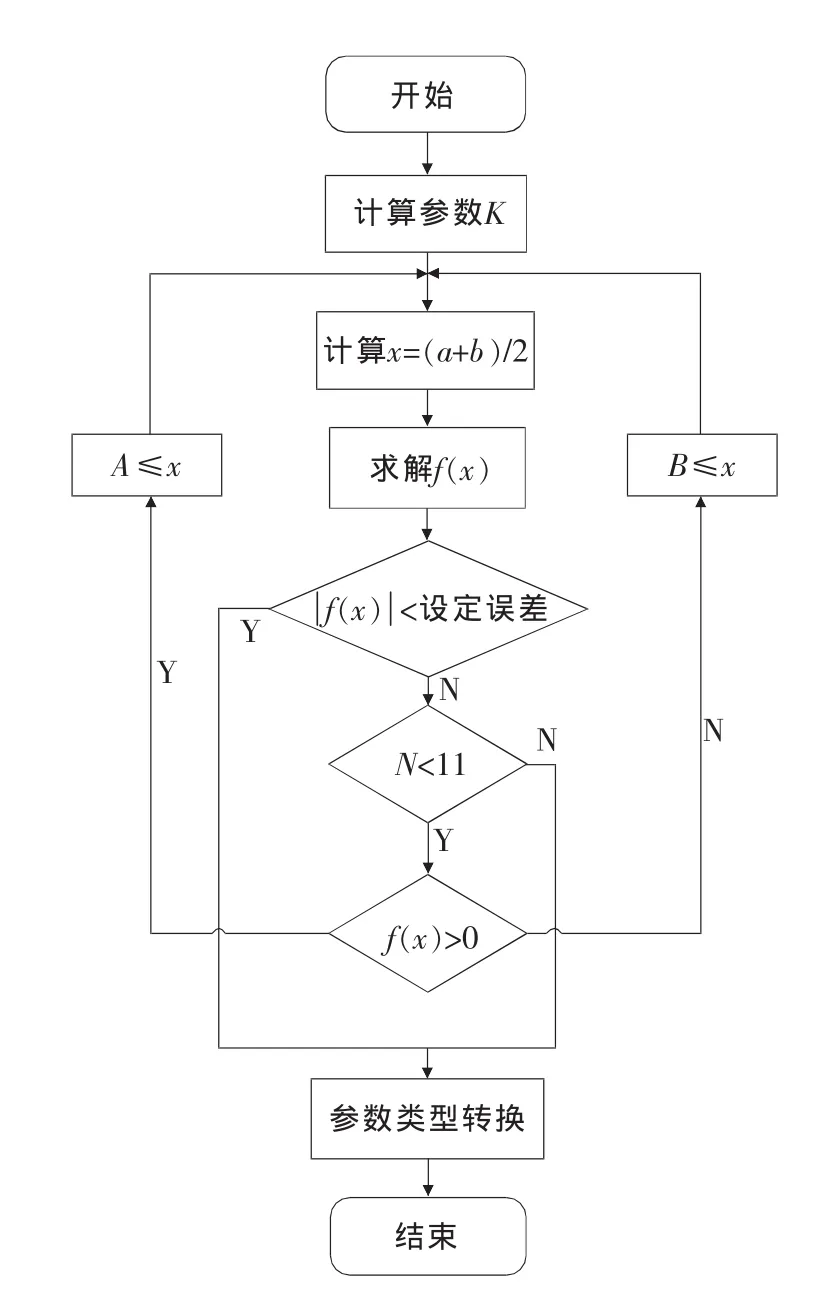
图4 二分法软件流程图
将式(6)代入式(5)后得到
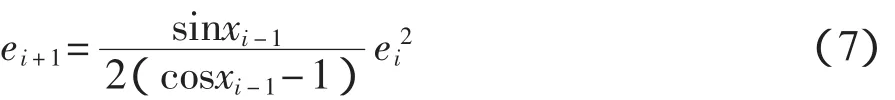
x∈[2αD,2π],再利用式(7)不难证明,存在 1 个正常数 C,满足式(8):
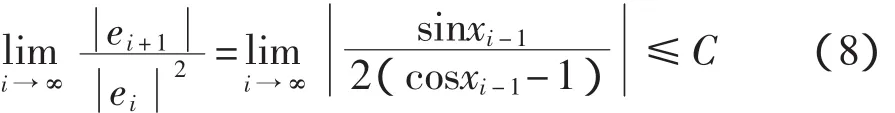
式(8)的数学意义是:该设计中f(x)使用牛顿迭代公式的收敛速度至少是二阶的。
牛顿迭代法初始迭代公式如下
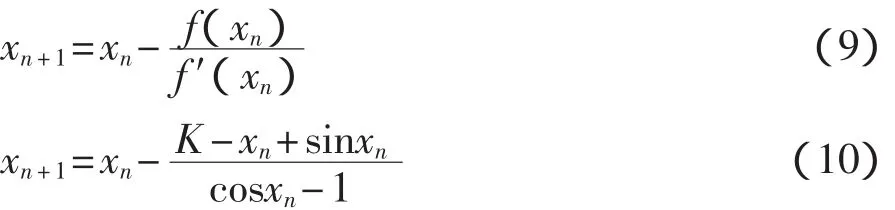
设定的初始点为π/2。流程图如图5所示。
2.3 弦截法及相应算法
弦截法是利用差商
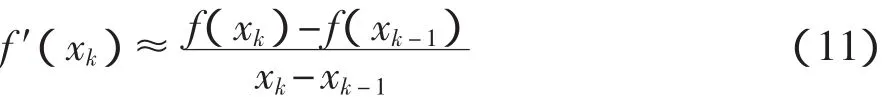
替代式(9)中的f′(x),得到
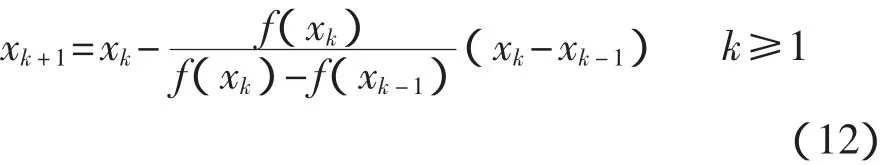
计算开始时需要指定2个初始点,分别为π/2和π/4。
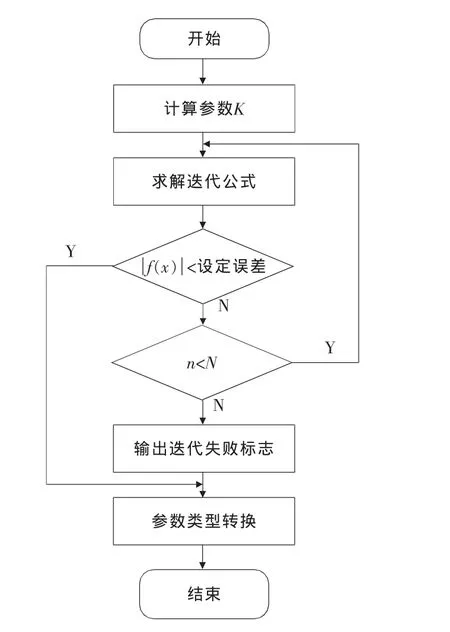
图5 牛顿迭代法流程图
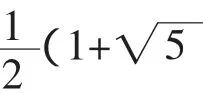
3 硬件实验平台
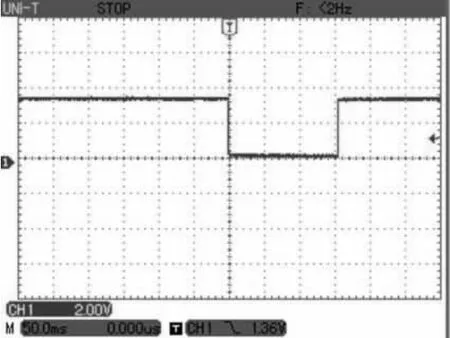
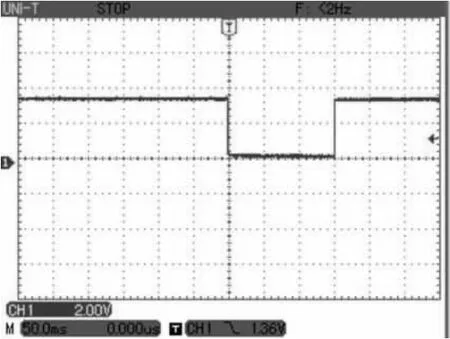
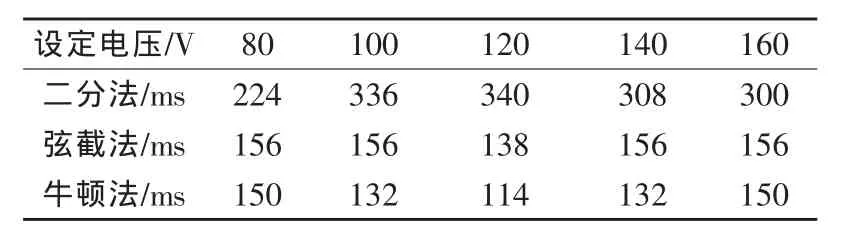
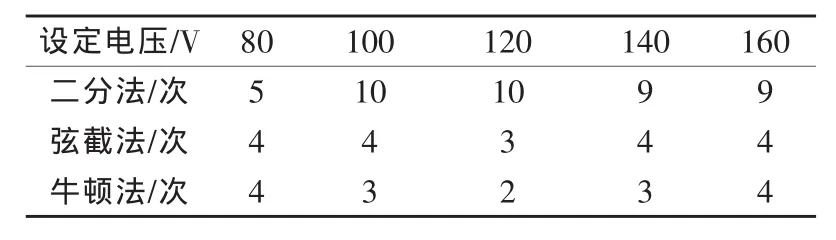
使用可控硅拼波调压系统中的控制板作为实验板,其中DSP的工作频率为130MHz,变压器抽头电压分为 4档:170V、66V、34V、25V。两档拼波电压的选择需要根据用户设定电压的大小去确定,即U1 实验方法:在CCS3.3开发环境下,利用IQmath库函数编写3种算法的程序,手动输入设定电压值,分别计算拼波角度值。 需要记录以下数据: (1)根据芯片的2个GPIO口的电平变化[7],使用示波器实测DSP完成3种算法分别所需要的时间。为了获得更精确的单次计算时间,每次计算次数10 000次,准确度为0.1°。 (2)设定1个全局变量,并且通过CCS中的Watch Window去查看记录3种算法需要迭代的次数。 (3)分别记录3种算法在不同的设定电压值下计算出的拼波角度值。 图6 二分法计算时间图 图7 弦截法计算时间图 图8 牛顿法计算时间图 表1 3种方法不同电压的计算时间 表2 3种方法不同电压的迭代次数 表3 3种方法不同电压的计算角度值 当设定电压为80V时,通过示波器单次触发记录GPIO的电平变化,记录相应算法计算10000次的时间。图6为二分法计算电平变化图,可知计算时间为224ms;图7为弦截法电平变化图,可知计算时间为156ms;图8为牛顿迭代法电平变化图,可知计算时间为150ms。通过比较可知在计算设定电压为80V时,牛顿迭代法最快,弦截法与之相差很少,而二分法计算速度最慢。 从表1和表2可以分析得知: 二分法单次计算时间可达34μs,为牛顿迭代法的2~3倍,但是二分法算法比较简单,且总是收敛的。缺点是收敛太慢,计算次数多达11次,所以一般不单独将其用于求根。 牛顿迭代法的收敛速度是2次,所以计算速度是最快的,随着牛顿法的每次迭代,精度明显倍增。在该系统中,一般迭代2~3次便可以得到符合精度要求的角度值。 弦截法的计算速度比牛顿法慢,但比二分法快。弦截法的收敛率是超线性的,免去了求解一阶导函数的繁琐,对于一阶导数非常复杂的非线性方程,弦截法就非常有优势,但是每次计算需要指定2个初始值[8]。 从表3中3种方法不同电压的计算角度值可知,3种方法均能计算出要求准确度为0.1°的角度值。但是从牛顿法和弦截法的角度值可知,准确度可以达到0.001°,这两种方法用较少的迭代次数获得了比二分法更高的精度。 该文介绍了可控硅拼波调压系统中求解拼波角度的非线性方程的推导过程,以及求解非线性方程的3种算法的对比研究。其中式(4)的非线性方程是拼波控制的核心,可广泛应用于各种基于拼波理论的调压(调功)系统中。由于该系统实时性较强,所以最终选择牛顿迭代法。以牛顿迭代法作为求解非线性方程已经应用于实际的可控硅调压系统中,整个系统工作期间电压波形稳定,且最后的功率因数在90%以上。 [1]张康乐,雷凯.一种新型晶闸管拼波控制电路的设计[J].自动化信息,2008(10):35-37. [2] Texas Instruments Incorporated.TMS320C28x系列 DSP的CPU与外设(上)[M].张卫宁,译.北京:清华大学出版社,2004:98-119. [3]李蒙,雷凯.基于DSP的高效可控硅交流调压系统的研究[J].自动化信息,2009,1(2):36-38. [4] Texas Instruments Incorporated.C28x IQmath Library[M].Dallas:Texas Instraments Incorporated,2008:21-24. [5] Nenadic N M,Mladenovic S B.Fast division on fixedpoint DSP processors using newton-raphson method[C]∥IEEE,Computer as a Tool.Eurocon,2005:705-708. [6]Kincaid D,Cheney W.Numerical Analysis数值分析[M].王国荣,译.北京:机械工业出版社,2005:63-79. [7] Texas Instruments Incorporated.TMS320C28x系列DSP的CPU与外设(下)[M].张卫宁,译.北京:清华大学出版社,2005:562-571. [8] 王沫然.Matlab与科学计算[M].北京:电子工业出版社,2004:98-101.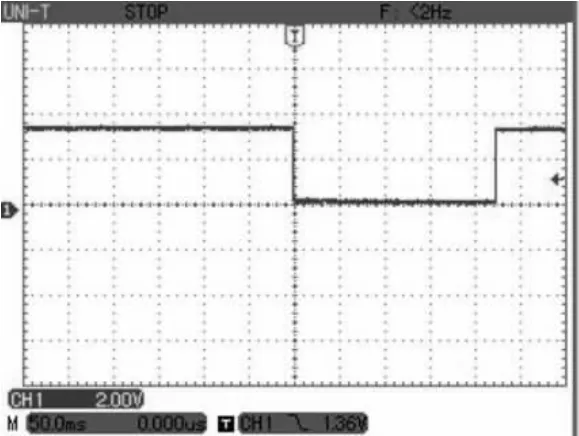

4 结果比较分析
5 结束语
