伪码调相连续波雷达模糊函数推导及仿真分析
2011-04-26曹军亮牟连云杨网成
曹军亮,牟连云,杨网成,杨 慧
(海军指挥学院,南京 211800)
0 引 言
连续波雷达具有优良的测速功能,由于其方便实现,结构简单,在雷达发展早期得到了广泛的应用,但由于其不能实现测距,因而在脉冲雷达出现后就逐渐淡出了人们的视野。直到近些年来,战场电磁环境日益复杂,干扰与反干扰愈演愈烈,对雷达已经提出了更高的需求,连续波雷达大的平均功率、高的占空比及用伪码进行调相实现测距使其在抗干扰中独胜一筹。
1 伪码调相连续波雷达原理
伪码调相连续波雷达是相位编码连续波雷达中的一种,通常其采用相关性比较好的编码来实现连续波的调相,不同的编码性能决定了该型雷达的性能和信号处理方式。各种编码如:m序列,也称为最大长度序列;Barker码,是一种相关性非常理想的码型,但到目前只找到最长为13位的码字;Taylor四相码,是由半余弦子脉冲(底宽为2T)经抽头延时(抽头间隔T)加权网络产生,是由二相编码经二四相转化器转换而来,具有二相码的性质,又不乏其独特之处。
本文的推导和仿真采用了Barker码和m序列,通过对它们的模糊图、相关性、零多普勒和零时延图的仿真与分析,得出采用序列更长的码型是伪码调相连续波雷达实现远距离测距的必然需要。
伪码调相连续波雷达的工作原理如图1所示,伪随机码产生器产生类似“白噪声”的伪随机码对本振信号进行调相,形成伪码扩频信号,伪码扩频信号经环流器在发射阶段从天线发射到空间;回波信号通过低噪声放大器将微弱的高频信号功率放大,然后与本振信号多次混频,经视频放大器将回波信号与延时的伪随机码在匹配滤波器中进行匹配滤波(即进行相关),从各相关器中出来的信号在多普勒滤波放大器组中进行多普勒滤波并放大,从多普勒滤波放大器组出来的信号再进行数据分选与分析。

图1 伪码调相连续波雷达工作原理图
伪码调相连续波雷达工作流程相对比较简单,主要特点是:
(1)隐蔽性。伪码调相连续波雷达发射的信号是伪随机码相位调制的时间连续波形。它是一种非脉冲波形的雷达信号,其平均功率等于峰值功率,故而具有极好的隐蔽性。
(2)良好的测距特性。上个世纪60年代,美国已经在Goddard测距和跟踪系统中采用了伪随机码测距原理,对深空目标进行测距跟踪。伪码调相连续波雷达测距是通过伪随机码良好的相关性来实现的。伪随机码具有随机特性,特别是它具有类似于δ函数的自相关函数,使它具备了作为测距信号的条件。伪码调相连续波雷达是用码字对载频信号调相后作为发射波形的雷达,这种具有较大时宽带宽积的雷达波形不仅克服了普通脉冲雷达的矛盾,而且极大地提高了雷达的测速和测距的精度;特别是当目标距离很远时,用一个很长的伪随机码可以同时达到精确和无模糊测距的双重目的。因此,伪随机码特别适合用于卫星、飞船等的轨道测量、导航和射电天文领域。
(3)伪码调相连续波雷达的抗截获特性。伪码调相连续波雷达是一种理想的低截获概率雷达(LPI),其具有非常理想的时宽带宽积。根据信息理论,大频带宽度的伪码调相连续波雷达具有更大的熵,有“白噪声”的统计特性,能实现扩频的性能。从截获接收机的截获特性看,极强相关性和更长的码字将会增大截获接收机的数据处理容量,迫使截获接收机数据处理能力下降,而且低密度的功率谱使截获接收机很难发现雷达信号,如果雷达进一步采取功率管理或者参数捷变等,就会更加增大被截获的难度。
(4)抗干扰特性。伪码调相连续波雷达信号是一种扩频信号,即把相关性能好的伪随机码在天线之前发射链路的某处引入,则发射到空间的雷达信号将扩散到一个更宽的频带中,降低了单位频带上的能量,在接收链路中对回波信号进行解扩,解扩的结果是使信噪比提高了N倍,更容易取出有用的回波信息。显然扩频可使总的辐射信号功率保持不变,而平均功率密度大大降低,这将减少雷达信号被截获的可能性,即使被敌方截获了,但由于信号编码的作用,会迫使敌方被动采用扫频式干扰,从而将降低干扰机的效能。在接收端对信号检测,必须实现同步解调,进行相关接收。相关解调完成由频谱扩展至压缩的频带转换过程。在相关恢复载波后,频域匹配滤波器可以采用单峰窄带低副瓣滤波器,有很高的速度分辨率和处理增益,可以滤除不同频率的有源干扰。对于在空间撒布的箔条、角反射器等无源干扰,由于运动速度不同,多普勒频率不一样,可以依靠连续波雷达速度分辨力高的特点,区分出真实目标和无源干扰假目标。对于施放的窄脉冲有源干扰,由于与信号不相关,通过数字信号处理过程的累积作用,使其窄脉冲有源干扰在输出端消失。
2 伪码调相连续波雷达模糊函数
模糊函数是衡量雷达发射波形特性的最好工具,我国在20世纪70年代末由张直中等人统一了模糊函数的定义。模糊函数主要是为了衡量信号对2个具有不同距离、不同速度的目标的分辨能力。
其定义为:

有些参考文献也将其定义为:

设伪码调相连续波雷达发射信号的复数形式可表示为:
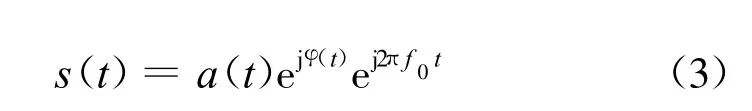
则其复包络信号形式可以表示为:
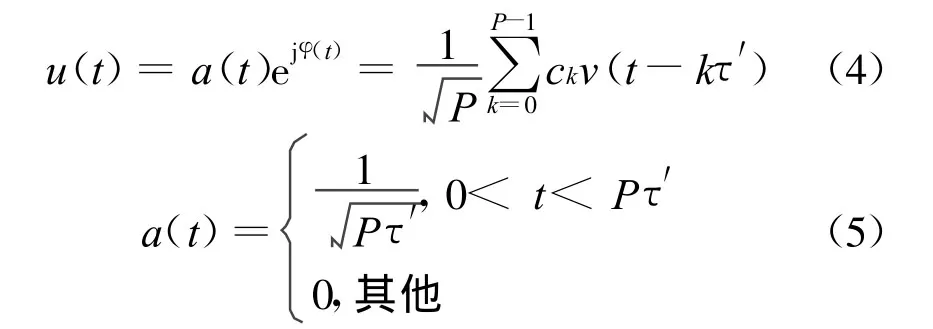
式中:P为m序列的长度;τ′为m序列的码子宽度;φ(t)为 0或者π,用二进制序列可以表示为:ck=ejφ(t)=+1,-1;v(t)为子脉冲函数,ck为m序列的各个码子;a(t)为矩形包络。
上式冲击函数形式为:

由于模糊函数也可以表示为卷积的形式,如:

则根据式(9),伪码调相连续波雷达的模糊函数可以表示为:
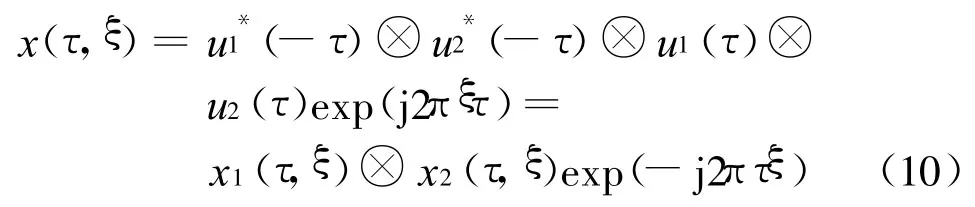
式中 :x1(τ,ξ)、x2(τ,ξ)分别为u1(t)和u2(t)的模糊函数,由于u1(t)为单脉冲函数,则从文献[10]可知,其模糊函数为:

式中:|τ|≤τ′,即在一个脉冲内,而在脉冲之外则模糊函数为0。

由于x1(τ,ξ)的推导只限在单脉冲中,将其扩展到P-1个脉冲,则伪码调相连续波雷达的模糊函数可以表示为:

3 伪码调相连续波雷达模糊函数仿真与分析
下面对13位Barker码和63位m序列调相连续波雷达信号(主频为10 GHz,码元宽度为50 ns)进行了重点分析。图2是13位Barker码的自相关函数图,从图中可以看出,13位Barker自相关函数主瓣比较尖锐,主瓣宽度为2△τ,旁瓣为△τ,主瓣峰值为13,而旁瓣为1,旁瓣衰减为-22.3 dB。虽然Barker旁瓣衰减相对比较小,但其长度却比较短,很容易被敌方侦破,而其-22.3 dB的旁瓣衰减也达不到雷达的要求,因此必须在匹配滤波之后对信号进行旁瓣抑制。
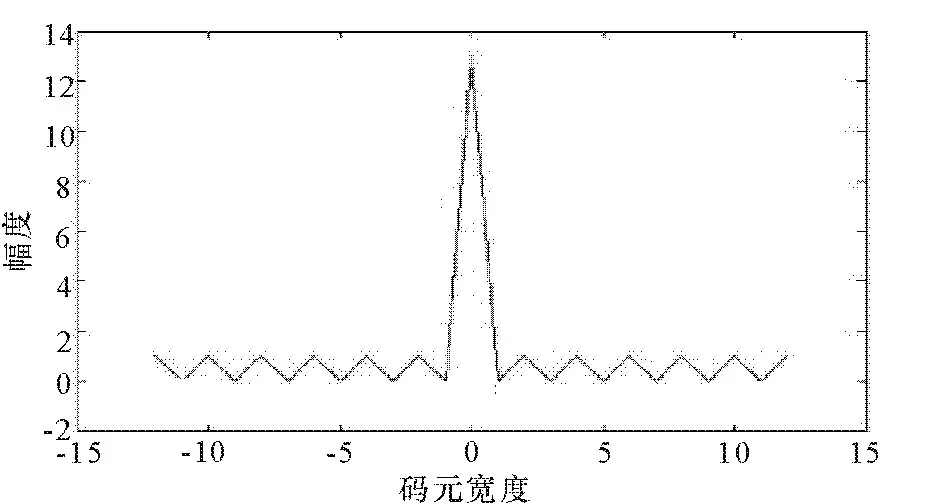
图2 13位 Barker的自相关图

图3 63位m序列自相关图
图3是63位m序列的自相关函数图,显然63位m序列的主瓣值更大,但旁瓣值也不小,最好旁瓣衰减为-19.1 dB,高于13位Barker的旁瓣衰减,因而在数字信号处理阶段必须加入旁瓣抑制电路。
图4是采用13位Barker码的模糊函数图,从图中可以看出Barker信号的模糊函数由于周期的原因呈“钉齿”状,虽然主峰很窄,但周期出现会严重影响雷达的测距。从图5的零多普勒截图就可以看出采用这种编码的雷达周期距离模糊严重影响测量回波信号的距离分辨力,从测速角度和多普勒分辨力角度来看,连续波编码信号无疑是一个更好的选择,从图6可以看出,其主峰值较高而旁瓣甚小。
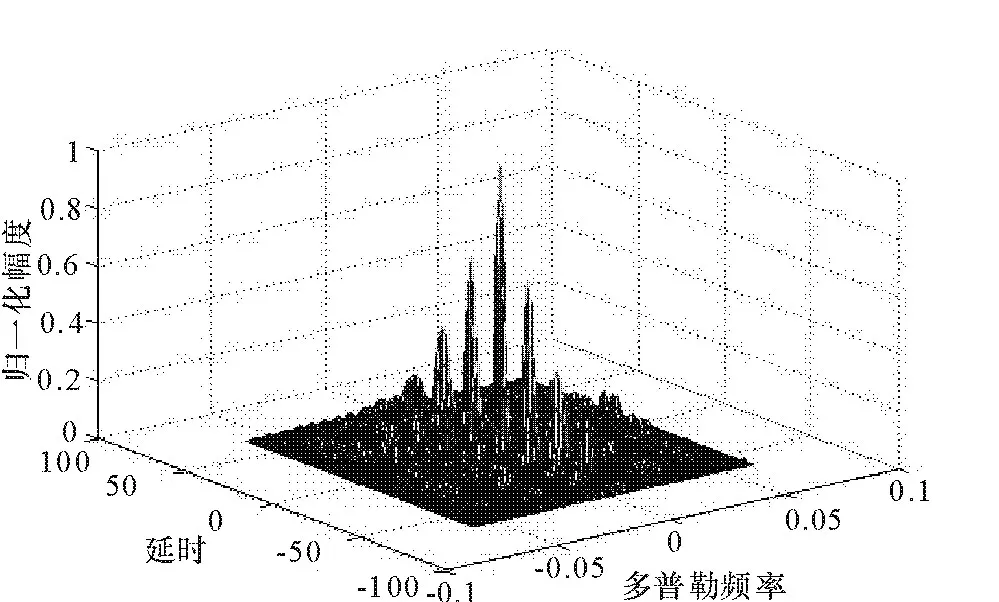
图4 采用13位Barker的伪随机连续波雷达模糊函数图
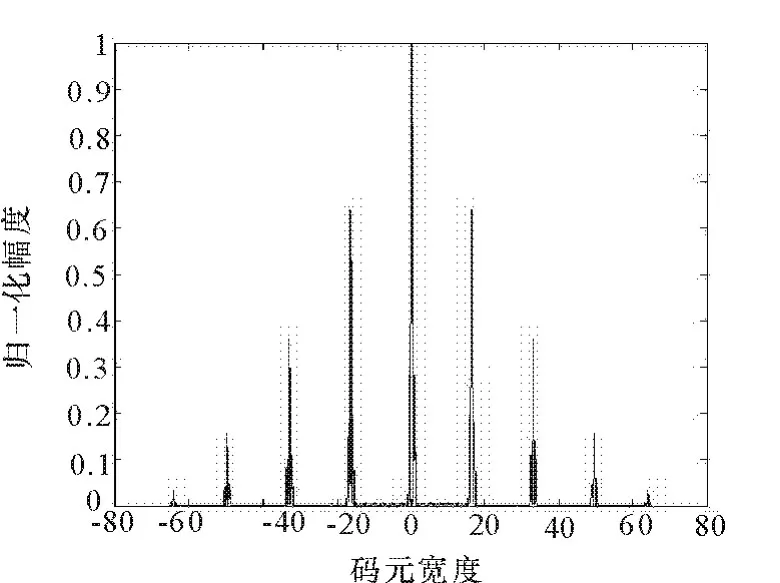
图5 13位Barker码零多普勒截图

图6 13位 Barker码零时延截图
为了更好地反映长码对编码连续波雷达有更好的分辨力,这里对63位m序列调相的信号形式进行了仿真。图7与图4对比,很明显,63位m序列调相信号模糊函数呈“图钉”型,而且在其1个周期内,产生很小的距离旁瓣,如图8所示。显然使用63位m序列调相信号的测距精度更高,距离更远。而图9却反映出其零时延却有比较大的旁瓣,影响了雷达的测速和多普勒分辨力的性能,必须进行多普勒补偿。

图7 63位m序列的伪码调相连续波雷达模糊函数图

图8 63位m序列零多普勒截图
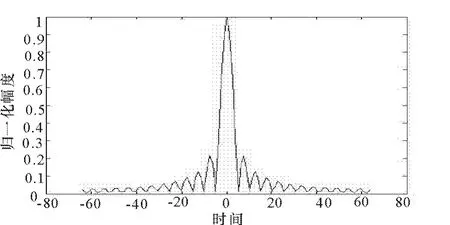
图9 63位m序列零时延截图
4 结束语
伪码调相连续波雷达具有检测灵敏度高、抗人为干扰能力强等特点,但从上面仿真可以明显看出其距离副瓣的存在严重影响了雷达测距和测速的精度,因而也将会减小抗分布式杂波干扰能力,所以必须在信号处理时加入距离旁瓣抑制电路,或者寻找相关性更好的码型,如有些文献中提到的计算机优选码型等。
[1] 李勇.连续波雷达穿墙探测技术研究[D].南京:南京理工大学,2009.
[2] 张永胜.伪码调相连续波雷达的性能与应用研究[D].南京:南京理工大学,2004.
[3] 岳涛.X波段伪码调相相控制导雷达信号处理方法的研究[D].哈尔滨:哈尔滨工业大学,2006.
[4] 李栋,刘进江.m序列的Matlab仿真与实现[J].重庆工学院学报(自然科学),2008,22(4):139-141.
[5] 丁晓辉,黄双华.Taylor四相码信号及其模糊图的绘制[J].舰船电子对抗,2005,28(2):26-28.
[6] 王李军.伪码定距及数字相关技术研究[D].南京:南京理工大学,2003.
[7] 易正红.相位编码雷达信号特征研究[J].电子对抗技术,2002,17(2):7-10.
[8] 黄鹏刚.低截获概率雷达技术研究[J].现代电子技术,2003(18):24-25.
[9] Bassem R Mahafza.雷达系统分析与设计[M].北京:电子工业出版社,2008.
[10]李国平.雷达脉冲压缩中相位编码信号旁瓣抑制的研究[D].辽宁:大连理工大学,2000.
