基于变化率的单站无源定位技术研究

毛 虎,杨建波,赵利杰

（1.空军航空大学,长春 130022；2.解放军93846部队,昌吉 831100）

0 引 言

传统的测向交叉定位需要进行多次测量,而且无法得到目标距离测量信息,使其定位精度和速度的进一步提高陷入瓶颈。近年来,单站测变化率的无源定位方法成为研究的热点,该类定位法应用的前提是定位站与目标之间必须要有相对运动。目前,研究较多的是机载侦察测向设备对地面固定或慢速移动目标的无源定位。由于该类定位法可以得到目标到定位站的距离,所以定位精度较高,定位速度较快。国外已将单站测变化率无源定位系统列为发展的重点,并已经进入工程应用阶段。鉴于此,本文通过分析机载单站测多普勒变化率、测角测相位差变化率、仅测相位差变化率定位技术和多普勒变化率、相位差变化率的测量方法,为单平台测变化率无源定位技术的工程实践提供理论参考价值。

1 测多普勒变化率无源定位

如果载机和目标辐射源之间存在径向运动,那么就会产生多普勒频移,可利用多普勒变化率来实现对目标辐射源的无源定位。

1.1 机载单站测多普勒变化率无源定位

先分析地面固定侦察站情况,再通过坐标变换将其变换到载机坐标系中。设目标在地面固定坐标系中坐标为（x,y,z）,相对地面侦察站的方位角为β,俯仰角为ε,多普勒频率fd与径向速度的关系为:

式中；f为目标辐射源频率；c为电磁波传播速度。

对式（1）求导得:

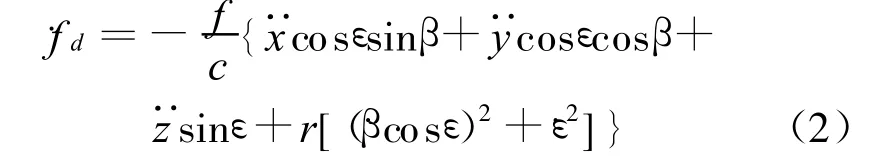
一般情况下,目标距侦察站的距离较远,目标的加速度扰动对定位的影响很小,可假定目标为匀速运动,则从式（2）可得到多普勒变化率测距的公式:

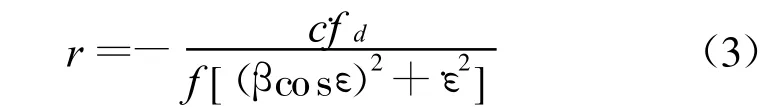
从而得到多普勒变化率无源定位的公式:

将目标的位置矢量变换到载机坐标系中,假设i时刻在地面固定坐标系中载机的瞬时位置为（xOi,yOi,zO i）,姿态信息为滚动角θi,俯仰角 ηi和偏航角γi,地面目标的瞬时位置为（xTi,yTi）,在载机坐标系中的目标位置记为（xi′,yi′,zi′）,则可得到如下的关系表达式:

1.2 多普勒变化率的测量

在多普勒变化率无源定位中,多普勒变化率的精确测量是定位算法能够实现的关键。到达信号频率fr应该由辐射源射频fs和目标径向速度导致的多普勒频率fd组成,即fr=fs+fd。对其求导得﹒fr=﹒fs+﹒fd,当信号射频不变 ,即 ﹒fs=0 时 ,﹒fr=﹒fd,可以通过测量 ﹒fr获得﹒fd。目前,主要采用的是基于延迟相乘的多普勒变化率提取技术,其原理框图如图1所示。

图1 多普勒变化率提取原理框图

设输入信号st=Assin（2πfrtt+φ）,经过延迟后的信号st-τ0=Assin[2πfrt-τ0（t-τ0）+φ],相乘并经过低通滤波器后得:

根据微分定理 ,frt-frt-τ0=﹒frtτ0,因此式（7）中的瞬时频率可表示为:

假设在处理观测时间t∈[0,T]内,频率变化率﹒frt基本不变≈0）,则可得 :

由上式可知信号的频率ft是多普勒变化率﹒fd在延迟时间τ0上的积累值,通过测量ft可以获得﹒fd,其精度取决于ft的测量精度 ,且 τ0 越大,ft越大,越有利于测量。

2 测角测相位差变化率无源定位

测角测相位差变化率无源定位是建立在干涉仪测向和相位差变化率测距基础上的一种定位方法。利用载机平台上携带的干涉仪天线阵,获得辐射源来波的相位差φ和相位差变化率信息﹒φ,进而从相位差与相位差变化率中解算出辐射源对于观测平台的方位以及辐射源与载机平台之间的径向距离,从而实现对辐射源的无源定位。

2.1 机载L阵三维测角测相位差变化率无源定位

对于三维来说,可以利用载机所携带的正交二维干涉仪获得目标辐射波的相位差和相位差变化率φx（t）、﹒φx（t）、φy（t）、﹒φy（t）,从而计算出辐射源的方位、俯仰以及距离信息,实现对辐射源的定位。

设载机坐标位置为（xOi,yOi,zOi）,目标相对于机身观测平台的方位角和俯仰角分别为β（t）、ε（t）,则机身轴方向二元天线阵和与其垂直的二元天线阵接收目标来波信号的相位差变化率分别为:

由式（10）、（11）和相位差 φx（t）、φy（t）计算公式可得:

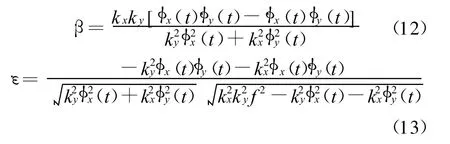
由几何关系可推导得:

可以看出,式（16）、（17）代表一个极坐标系下的球方程,它与目标方位角βi和俯仰角εi所确定的定位线的交点就是目标辐射源的位置。另外也容易看出,这种定位法是一种实时的定位方法。

2.2 一维干涉仪三维测角测相位差变化率无源定位

在三维空间中,可以仅采用一维干涉仪测量圆锥向角代替方位角和俯仰角,并与相位差变化率及目标高程先验信息组合实现对目标的瞬时定位。

图2为一维干涉仪测量系统示意图。

图2 机载三维空间测量模型

假设在k时刻,载机位置为 Xo,k=[xok,yok,zok]T,其姿态信息为方位角 αk,俯仰角 βk,滚转角εk,载机上一维干涉仪基线的安装角以干涉仪基线在机体坐标系中的方位角αa和俯仰角βa来度量,并且认为在飞行过程中安装姿态角始终保持不变,记干涉仪基线指向方向的单位矢量为Dk,静止目标位于XT=[xT,yT,zT]T,记目标视线方向的单位矢量为Lk,θk为干涉仪测量的圆锥向角。干涉仪基线的指向方向Dk、目标视线方向Lk和圆锥向角θk可分别表示为:

令D=[Dx,Dy,Dz]T,L=[Lx,Ly,Lz]T,则根据圆锥向角θk的计算公式可得到:

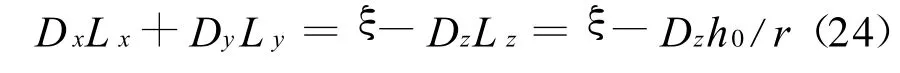
式中:h0为目标高程信息。

令 ω=[ωx,ωy,ωz],Vo=[vx,vy,vz]T,将圆锥向角θk的计算式带入式（22）得:

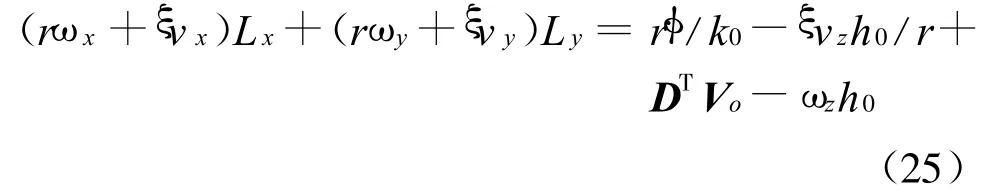
联立式（24）和（25）,可得到Lx和Ly的数学表达式。由于LkLTk=1,可得到:

将Lx和Ly的数学表达式带入式（26）可得到关于r一元四次方程,解此方程可得到目标距离r,进而带入Lx和Ly的数学表达式,得到Lx和Ly,即求得目标位置。

通过式（22）可以发现相位差变化率主要由载机位置变化dLk/dt引起的相位差变化率和载机姿态变化引起的相位差变化率dDk/dt两部分构成。在载机姿态变化过程中干涉仪基线相对于目标辐射源发生了较大旋转,这种旋转放大了相位差变化率。在干涉仪相位差变化率测量精度相对固定的情况下,如果相位差变化率本身量值越大,则其相对估计误差越小,定位精度越高。因此,该方法可利用传统方法中认为的载机姿态抖动和变化是对定位的“有害”信息,来获得大的相位差变化率,从而提高定位精度。

2.3 相位差变化率提取方法

相位差变化率主要通过相位差序列获得,目前从相位差序列中提取相位差变化率的方法主要有差分、卡尔曼滤波及线性拟合等,卡尔曼滤波法虽然提取精度较高,但比较复杂,难以满足实时的要求。可以先进行差分,然后对差分后的结果进行线性拟合,也可以得到较高精度的相位差变化率,且时效性更好。

相位差变化率可以理解为相位差的“频率”,可写出其Cramér-Rao下界为:

式中:T=NTs为总的观测时间,N为采样个数,Ts为采样间隔；rSNR为信噪比。

从式（27）可以看出,增加观测时间能获得高精度的相位差变化率,假设发射信号为等间隔的脉冲信号,对每个脉冲信号可得到一个相位差值,积累后得到相位差序列,对每个序列对应位置的相位差进行相减,即Δφ（i）=φN+1（i）-φN（i）,i为相位差序列中第i个脉冲指数,进行平均处理后相位差变化率为:

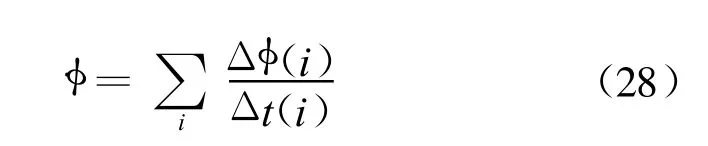
式中:Δt（i）为两序列第i个脉冲中点的时间差。

需要注意的是,延长观测时间虽然可以提高差分法测量精度,但当时间较长时相位差有可能不是线性变化,所以要合理选择观测序列长度。对差分后得到的相位差变化率进行线性拟合得到相位差变化率与时间的关系曲线,进而得到高精度的相位差变化率测量数值。

3 仅测相位差变化率无源定位

在三维空间中,采用测角测相位差变化率实现无源定位均需利用目标的角度测量信息,再结合相位差变化率参数才能解算出目标位置。这导致长短基线干涉仪系统较为复杂,并需要精确求解相位差模糊。为了减少设备载荷、降低硬件需求,文献[1]、[8]～[11]提出了不利用角度而仅利用相位差变化率测量信息进行机载单站无源定位的新方法。

3.1 三角基线测相位差变化率无源定位

机载单站三角基线测相位差变化率定位模型如图3所示。三天线分别为A、O、B,两基线互相垂直,目标辐射源相对于载机的方位角为β,俯仰角为ε,载机与辐射源的距离为r。

图3 单站三维空间定位示意图

记天线O、B的相位差为 φ1,天线O、A的相位差为φ2,可得到:

联立式（29）～（31）,可得一个关于方位角β、俯仰角ε、方位角变化率﹒β、俯仰角变化率﹒ε的方程组,解之可得方位角β和俯仰角ε,由r=z0/sinε得到距离r,实现对目标辐射源的定位。

3.2 长基线测相位差变化率无源定位

假设载机的高度可忽略不计,β（t）为来波方位角,α（t）为机载干涉仪的姿态角,φ0为通道不一致带来的固定相位误差,则两天线的相位差可表示为:

式中:d为基线长度；f为频率；c为光速。

对式（33）求导,可得在k时刻相位差变化率为:

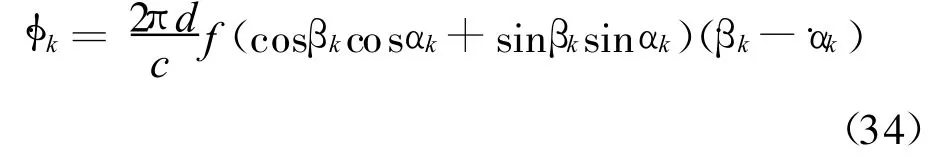
假设在k时刻,载机的位置坐标为（xk,yk）,地面固定辐射源的位置为（xT,yT）,则方位角 βk和﹒βk分别为:

从式（37）可知,﹒φk是目标位置的非线性函数,理论上由2个不同时刻的﹒φk解非线性方程组即可解出目标的位置。在载机飞行过程中,一般可以测量得到多个时刻的相位差变化率,这时可以采用非线性最小二乘、扩展卡尔曼滤波（EKF）等非线性跟踪滤波方法求解目标位置,也可以构建代价函数,采用网格搜索的方法直接寻找代价函数最小点来搜索目标位置。

采用非线性最小二乘法进行滤波时,如果测量得到k个相位差变化率,给定t0时刻的一个目标位置初始值^X0,通过迭代递推可以得到目标位置X在k时刻的非线性最小二乘估计:

采用非线性最小二乘、扩展卡尔曼滤波（EKF）等非线性跟踪滤波求解目标位置的方法,性能严重依赖初始化的结果。由于无法提供目标方位角度信息,仅依靠相位差变化率测量无法得到比较准确的目标位置来当作初始估计信息,因此可采用近似最大似然估计的网格搜索算法对目标实现定位。

对上式取对数可得到对数似然函数:

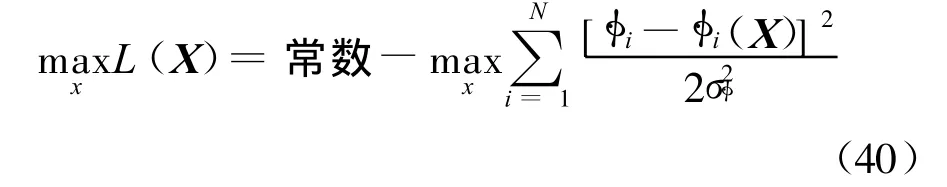
最大似然估计的意义在于全空间范围内搜索X,使得似然函数最大。因此,可将待定位目标所在空域离散化为网格点,通过循环遍历对每个网格点根据式（23）计算相位差变化率,并与实际系统获得的相位差变化率测量值比对,即可获得整个网格化空域内的似然函数分布情况,而满足式（40）的网格点即为待定位目标的位置。可以看出,网格的最小尺寸决定了该方法的最优定位性能,在没有角度信息的情况下,该算法一般采用均匀划分网格。

4 结束语

测多普勒变化率定位与测相位差变化率定位相比,不需要目标和侦察站之间的相对速度,对运动目标而言,目标和侦察站的相对速度已知的前提很难满足,所以测多普勒变化率定位算法可观测性更强。对地面固定目标,一维干涉仪体制测角测相位差变化率定位算法采用圆锥向角代替方位角和俯仰角,定位系统设备相对简单,在工程实践中不受载机体积和载荷的限制,而且可以充分利用载机姿态抖动和变化这些传统意义上的“有害”信息来提高定位精度。仅用长基线测相位差变化率定位不需要解模糊操作,计算量相对较小,采用逐渐逼近最大似然估计的网格搜索方法由于不需要目标位置的初始估计信息,其性能要优于最小二乘、扩展卡尔曼滤波等非线性跟踪滤波方法。改进多普勒变化率、相位差和相位差变化率测量方法,提升其测量精度是测变化率无源定位获得高精度的关键。

[1] 朱伟强,黄培康,马琴.基于相位差变化率测量的单站定位方法[J].系统工程与电子技术,2008,30（11）:2108-2111.

[2] 王强,钟丹星,邓新蒲,周一宇.一维干涉仪体制运动单平台定位算法和仿真分析[J].系统仿真学报,2009,21（22）:7205-7210.

[3] 黄登才,丁敏.测相位差变化率无源定位技术评述[J].现代雷达,2007,29（8）:32-34.

[4] 牛新亮,赵国庆,刘原华,常虹.基于多普勒变化率的机载无源定位研究[J].系统仿真学报,2009,21（11）:3370-3373.

[5] 刘建,安智国.固定单站对运动目标的无源定位[J].中国电子科学研究院学报,2008,3（1）:60-64.

[6] 潘琳.干涉仪测向与相位差变化率定位技术[D].西安:西安电子科技大学,2009.

[7] Wang Junhua,Wang Yongsheng,Guo Tao,Wang Honghao,Wang Qiang.Rate of phase difference change estimation in single airborne passive locating system[J].ChineseJournal ofAeornauitcs,2009（22）:184-190.

[8] 郭福成,贾兴江,皇甫堪.仅用相位差变化率的机载单站无源定位方法及其误差分析[J].航空学报,2009,30（6）:1090-1095.

[9] 王强,钟丹星,郭福成,邓新蒲,周一宇.仅用长基线干涉仪测量相位差变化率的运动单站无源定位方法[J].信号处理,2009,25（8A）:566-569.