数控工作台单自由度直线运动单元速度环控制系统建模、仿真与分析

刘学军

（金堆城钼业股份有限公司，陕西华县714102）

0 前言

运动控制（包括轨迹控制、伺服控制）与顺序控制、过程控制、传动控制并列为典型的控制模式，是一直以来扮演重要支柱技术角色的自动控制系统，在许多高科技领域得到了非常广泛的应用，如激光加工、机器人、数控机床、大规模集成电路制造设备、雷达和各种军用武器随动系统以及柔性制造系统等等。

在这个实验系统的设计中，采用计算机上、下位机的协同工作的控制系统构成方式，下位机实现实时信号处理，实时控制，上位机具有功能选择、输入设定、操作命令、实时显示、报警、系统性能分析等功能。用户可通过计算机对控制系统发送指令，使电机按照用户的指令运转，同时电机的参数如转速、位置、转矩等信息通过数据采集系统采集到计算机中，形成闭环控制，采集数据可进行打印、曲线显示等处理。

本实验通过简单的数控工作台单自由度直线运动速度环控制系统的建模、仿真和分析，旨在分析自动控制原理在电机控制系统中应用规律及控制系统静、动态分析方法。

1 直线运动单元数学模型的建立

1.1 速度开环系统

1.1.1 模型方程

首先电机回路满足基尔霍夫电路定理：

电机电磁转矩与电流成正比：

Mm（t）=cm·ia（t）

电机转动产生的反电动势和电机转速成正比：

Ea（t）=ce·ωm（t）

电机的力矩平衡公式：

将4个微分方程进行拉普拉斯变换，得到一组线性方程：

Ua（s）=La·Ia（s）·s+Ra·Ia·（s）+Ea（s）

Mm（s）=cm·ia（s）

Ea（s）=ce·ωm（s）

Mm（s）=（Jα·s+Bm）·ωm（s）+Mc（s）

等效转动惯量：

代入如下数据：

计算得：Jα=1.1×10－4kg·m2。

0.080 2 v.s/rad齿轮减速比i 1 电压放大Apm额定电压U 24V 反电动势常数CB2.4电机电阻Ra 1.18欧 转矩常数Cm0.080 48 Nm/A电机电感La 1.37 mH 电机转子转动惯量Jm 0.9×10－4kg·m2丝杠导程p 5 mm 等效阻尼系数Bm0.001 5丝杠直径d 14 mm 速度放大增益Kw20丝杠长度l 360 mm 丝杠密度ρ 7.8 g/cm3工作台质量m215 kg

1.1.2 系统动态结构图

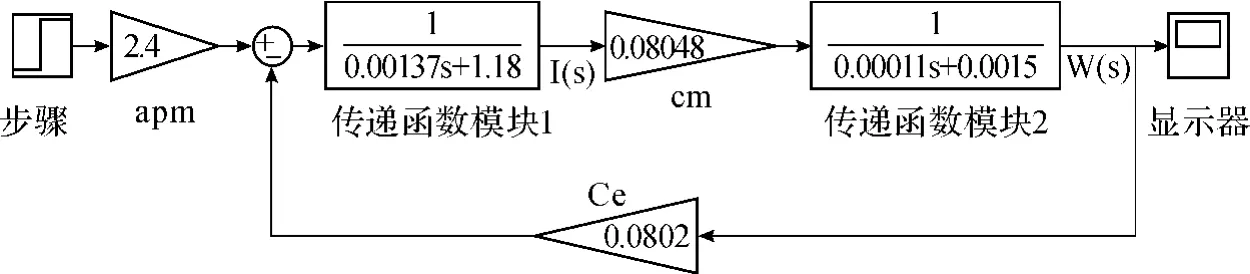
图1 速度开环系统动态结构图

1.1.3 系统传递函数

以给定电压为输入、以实际丝杠转速为输出，系统传递函数为：

1.2 速度闭环系统模型

速度闭环系统模型建立步骤与开环系统类似，只是加上一个反馈。

系统的动态结构图如下：

图2 速度闭环系统动态结构图

给定电机转速为输入、以实际电机轴转速为输出，求出系统闭环传递函数为：

2 模型分析

2.1 阶跃相应曲线

开环系统、闭环系统分别见图3、图4。

图3 开环系统

图4 闭环系统

2.2 稳定性分析

开环系统尼奎斯特线图，波特图见图5，闭环系统尼奎斯特图，波特图见图6。

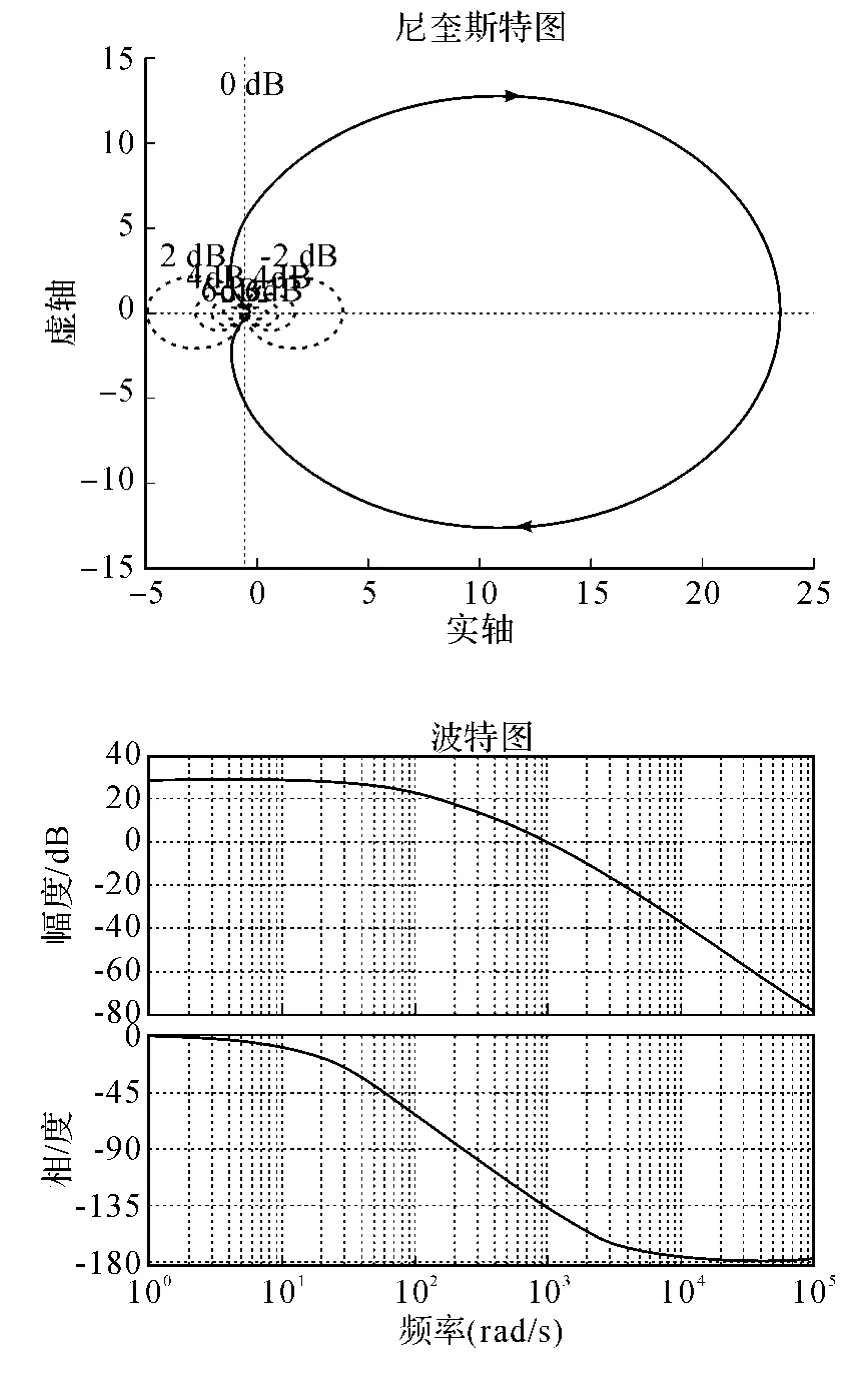
图5 开环系统尼奎斯特图，波特图

2.3 稳态误差分析

开环系统输入与输出的单位不一致，故无法判断稳态误差。

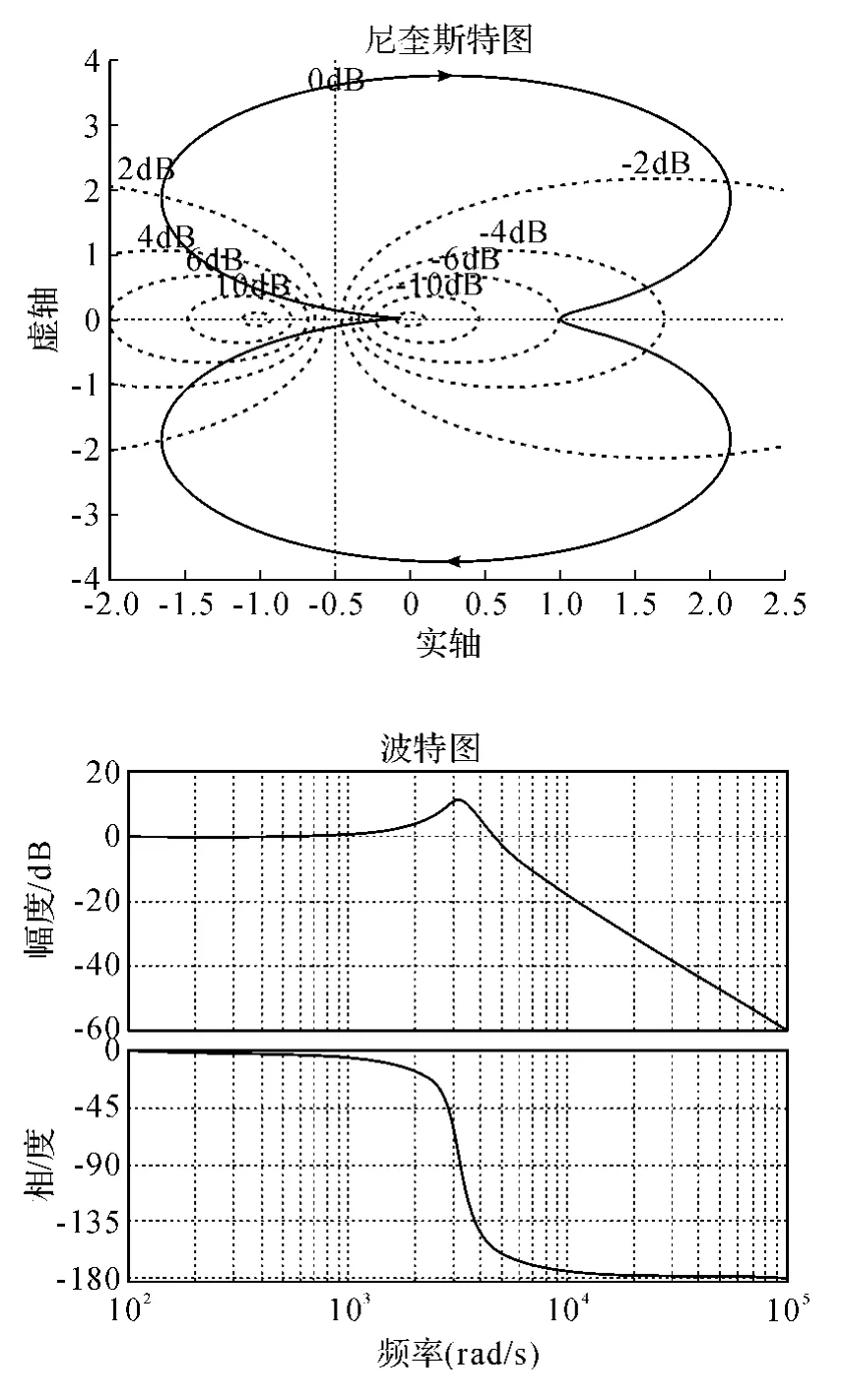
图6 闭环系统Nyquist图，Bode图

闭环系统在单位阶跃响应，按照图来看，系统并无稳态误差，但理论上稳态误差还是存在的，稳态值为：

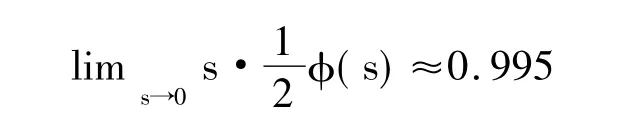
即稳态误差为0.5％。

3 固高XY工作台实践结果

直流伺服电机速度曲线见图7，电压分别为3 V、4 V、5 V、6 V、7 V。

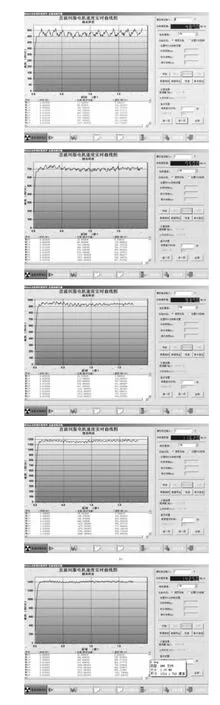
图7 直流伺服电机速度曲线（电压3 V、4 V、5 V、6 V、7V）

建立速度—电压图像：（横坐标ω/（rad/s），纵坐标U/V）

图8 速度—电压图像

拟合曲线斜率的倒数为电压增量与速度增量之比，值0.041 7，乘以放大倍数Kw为0.100 1，与Ce =0.080 2相近，外力矩的存在导致截距不为零，理论计算相差约0.022，实际相差为0.019 9。

闭环系统图像见图9。

图9 闭环系统图像

4 结论

通过实验数据可以得出：数控工作台单自由度直线运动单元速度环控制系统闭环系统在加了反馈之后相比开环系统较为稳定，随着输入电压的增大，输出电机转速也相应增大，呈线性相关。同时，输入电压越大，输出电机转速震幅越小。

［1］邓钟星.机电传动控制［M］.武汉：华中科技大学出版社，2007.

［2］胡寿松.自动控制原理［M］.北京：科学出版社，2007.