基于国家粮食储备监督的博弈分析

刘 佳,朱忠贵 (长江大学经济学院,湖北农村发展研究中心,湖北荆州402023)

近年来,由于世界粮食生产量低于消费量,不足的供给不断消耗着粮食库存,导致库存不断下降。根据联合国粮农组织估计,目前全球粮食储备已降至1980年以来的最低水平,仅能满足50多天世界消费,一场粮食危机正席卷而来。因此,做好粮食储备,是实现粮食安全一个重要前提。作为一个13亿人口的大国来说,拥有世界20%的人口,但只有9%左右的耕地,粮食安全至关重要。由于粮食储备库和粮食行政主管部门之间信息的不对称,故研究通过引入不完全信息静态博弈模型,并从这一角度出发,推导出了博弈空间,以期为国家粮食储备监督提供理论和现实的依据。

1 国家储备粮的信息不对称分析

一般来说,粮食储备关系到国家粮食安全,这种性质决定了政府机构 (粮食行政主管部门)或国有公司实施粮食监管的必要性。由于现实中信息不对称的存在,使得储备粮食实物的执行者 (即粮食储备库)和日常监督者 (即粮食行政主管部门)之间存在着复杂的博弈关系,从而造成粮食储备监管效率的降低、粮食倒卖现象严重等现象。作为粮食储备库更具有信息优势,其原因有二:一是国家粮食储备机构的消费性支出的需要,形成隐藏信息 (即逆向选择)的条件;二是粮食储备库的努力程度,即是否存在偷懒或投机行为的现象,形成隐藏行动 (即道德风险)的条件[1]。隐藏信息的问题主要因为粮食储备体系、市场需求条件、财务管理、地方性差异及轮换机制的不灵活,强调内部人员比外部人员更容易获知信息的优势[2];隐藏行动则是储备粮食的努力程度,即粮库的硬性条件及存粮的质量及保管行为难以准确观测,除了粮食储备库内部人员自己知道外,粮食行政主管部门对此知之甚少。这样一来,粮食储备库常常会利用自己的信息优势逃避监督或对抗处罚,以实现自身利益最大化,从而使得监督效率无法达到最优状态[3]。另一方面,从监督部门来讲,粮食行政主管部门对粮食储备库进行监督,在这一过程中会产生相应的管理成本,其成本的高低直接决定了监督部门实施粮食监管的难易程度,高昂的监督成本会降低监督部门的监督效率。

因此,如何寻找有效的降低或者最大限度的消除储备库与行政主管部门之间存在的信息不对称现象,就成为提高粮食监督部门工作效率的关键,也有助于督促粮食储备库提高储粮质量与数量。

2 国家储备粮博弈模型

2.1 模型假设

为了便于分析与研究,可将多重委托代理关系简化为粮食行政主管部门和粮食储备库为局中人[4],具体假设如下:

假设一:参与人由委托人和代理人两方构成,其中委托人为粮食行政主管部门,代理人为粮食储备库[5]。

假设二:粮食行政主管部门有2个策略可供选择,即监督和不监督。其中粮食行政主管部门在正常工作的情况下,其正常的工作收益为i;如果粮食行政主管部门进行监督,则同时需要付出相应的监督成本为c。

假设三:粮食储备库有2个决策可供选择,即投机和不投机。若投机,如果没有被发现,那么其可能获得收益为α;若投机被发现,那么被处罚款为θ;其中α≤θ(为了防止在投机被发现情况下,粮食储备库仍会从中受益)倘若不投机,那么其可能的收益为0。

假设四:如果粮食储备库进行投机行为,粮食行政主管部门不对其进行监督,有2种情况:其一是有人举报,使得粮食储备库的投机行为曝光(但此时尚未核实和尚未对粮食储备库进行处罚),这时粮食行政主管部门将被追究责任,即被处罚款为ε;其二是无人举报,粮食储备库的投机行为没有被发现,则粮食行政主管部门的收益仍为其正常收益,即i。

假设五:粮食储备库与粮食行政主管部门同时行动,则粮食储备库是否有投机行为、粮食行政主管部门是否进行监督、粮食行政主管部门是否发现问题、是否有人举报等都是不确定的。不完全信息静态博弈中参与人同时行动,每个参与人仅知道其他参与人的类型和概率分布。具体假设为,粮食储备库投机行为的概率为ρ(0≤ρ≤1),不投机的概率为1-ρ;粮食行政主管部门监督的概率为δ(0≤δ≤1),不监督的概率为1-δ;粮食行政主管部门监督时发现投机行为的概率为α(0≤α≤1),没有发现问题的概率为1-α;粮食行政主管部门不监督时有人举报的概率为β,没人举报的概率为1-β。

从上述分析中可以得知以下几个命题:

命题一:在委托代理关系中,粮食行政主管部门和粮食储备库在追求各自利益最大化时,双方存在着目标上的差异,双方在工作中不可避免的会产生各种矛盾,从而扩大内耗。粮食行政主管部门的问题是如何设计一套行之有效的监督机制,设法使粮食储备库只有在为保障粮食行政主管部门利益尽力工作时,实现其自身利益最大化[6]。

命题二:粮食行政主管部门的监督行为选择,与粮食储备库的投机行为选择均取决于模型中的参数值[7]。粮食行政主管部门监督行为的选择取决于其监督收益大小之比,而粮食储备库的投机行为的选择则取决于其投机行为收益与损失之比。因此,良好的制度设计应考虑监督博弈的混合策略解,尽量增加粮食储备库投机行为的惩罚力度,尽量减少粮食行政主管部门的监督成本,使其监督收益尽量增加,从而加大监督的力度[8]。

命题三:除粮食行政主管部门和粮食储备库的博弈双方之外,粮食储备库内部人员和社会公众的举报以及媒体监督作用,也会促进改善粮食行政主管部门的监督行为和效果,从而防止粮食储备库投机行为。

2.2 模型分析

(1)博弈模型及混合策略纳什均衡 根据上述假设可以得到委托双方的监督博弈模型,详见表1。

表1 信息不对称下的粮食储备监督模型

此时,粮食行政主管部门监督的期望得益为:

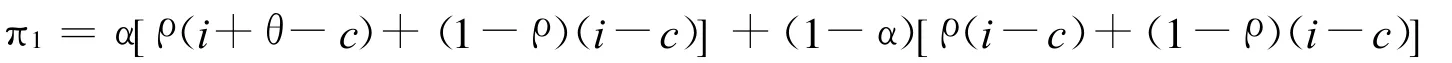
粮食行政主管部门不监督的期望得益为:

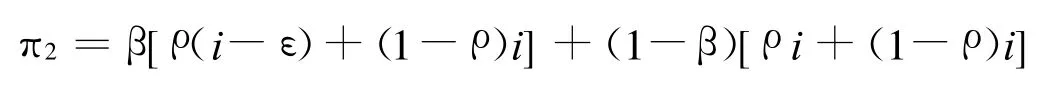
当π1=π2时,即粮食行政主管部门监督与不监督的期望得益相等时,可以得到:

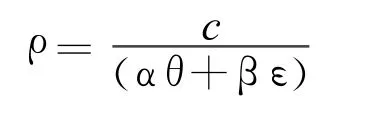
同理可得,粮食储备库投机与不投机的期望得益为:

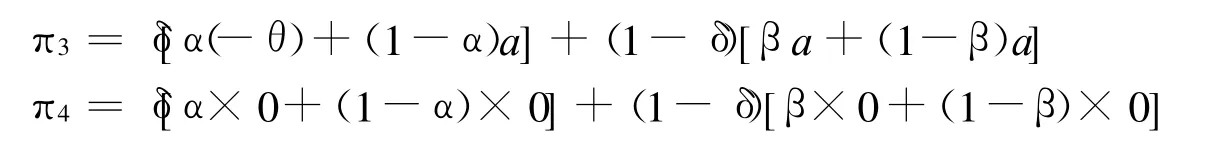
当π3=π4时,即粮食储备库投机行为与不投机的期望得益相等,可以得到:

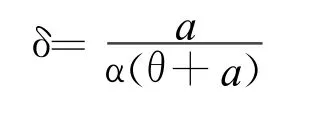
(2)要素变量与博弈解的关系分析 根据博弈模型可知,粮食储备库是否选择投机行为的理性行动决策取决于粮食储备库投机行为的期望得益与不投机行为得益之差值,即当δ=0时此时,粮食储备库的预期收益最大。当δ=1时此时,粮食储备库的预期收益则依赖于粮食行政主管部门发现投机行为的概率α,在一定程度上取决于监督部门人员的自身素质。若时,即粮库投机获得的期望更大,此时粮库会选择投机行为。所以粮食储备库投机行为的区间为。同理,粮食行政主管部门选择监督与不监督之差值,作为行政主管部门的理性行动的出发点,即。当 ρ=0时,。此时,粮食行政主管部门需付出成本c。当 ρ=1时若时,即粮食行政主管部门获得的期望更大,此时粮食行政主管部门会倾向于监督行为。所以,粮食行政主管部门监督行为的区间为:

综上所述可知,对于粮食行政主管部门来说,影响其期望得益的因素主要有监督成本(c),对粮食储备库的惩罚力度(θ),发现投机行为的概率(α),对自身的惩罚力度(ε)。降低监督成本,即均衡解ρ越小越好;行政主管部门加大惩罚力度(θ),以此来扩大监督行为的空间;粮食行政主管部门发现粮食储备库投机行为的概率α越大,即检查质量和水平较高,对投机行为的威慑作用就越大;另外,加强对自身的管制,为了防止行政部门内部人员犯错,追究行政部门的责任,加大对自身的惩罚力度ε,从而提高监督的质量。

对于粮食储备库而言,影响其期望得益的因素主要有发现投机行为的概率(α),对其惩罚力度(θ),因投机行为的收益a。当粮食行政主管部门提高自身质量时,发现投机行为的概率α越大,粮食储备库的投机行为区间越小;对投机行为的处罚力度加大,那么投机的风险就会加大,此时粮食储备库的投机行为就会有减少的趋势;若投机行为的收益降低,投机行为也将会减少。

此外,加大监督力度还有一个重要因素,那就是举报,当举报的概率(β)较高时,粮食储备库的投机行为就会降低,而此时粮食行政主管部门因举报属实的话要被追究责任,所以粮食行政主管部门也同样会提高自身素质,使监督更加有效。

3 对策

规范对储备粮的管理,加强对粮食储备库的日常管理,加大对粮食储备库投机行为的惩罚力度。加大对粮食储备库的惩罚力度可以起到双重作用,这种方式不仅可以压缩投机行为的空间还可以使监督更加有力。

加强粮食行政主管部门的监督力度,再提高监督质量的同时降低监督成本。提高监督质量的方法主要有2方面,一方面对现任人员进行职业培训和技术指导,增强学习,加强职业道德教育;另一方面可以计息吸收引进一批高素质专业人才。在监督质量提高过程中,监督成本在一定程度上呈上升趋势,但是,当监督质量达到一定程度时,由于内部人员整体素质的提高,使得监督效率上升,此时监督成本呈下降趋势。

依据博弈模型,得知建立良好的监督机制,不仅要对粮食行政主管部门进行再监督即对部门内部人员实行奖惩制度(ε),还要鼓励接受社会舆论,公众的监督(包括粮食储备库内部人员的监督)。社会的举报越多,举报几率越大即β越大,对粮食行政主管部门的惩罚力度越大,粮食行政主管部门的将会更努力的行使监督权,粮食储备库的投机行为也就会越小[9]。

随着科技的发展和计算机的普遍应用,更有助于创立公开透明的信息流通机制,使得粮食行政主管部门和粮食储备库之间信息流通顺畅,做到与市场同步。信息透明使监督者更容易了解粮食储备情况和流转现状。

[1](美)罗杰·B迈尔森.博弈论矛盾冲突分析 [M].北京:中国经济出版社,2001:110-112.

[2](美)罗伯特吉·本斯(Gibb).博弈论基础[M].北京:中国社会科学出版社,1999:120-125.

[3]朱志刚.我国粮食安全与财政问题研究[M].北京:经济科学出版社,2008:22-27.

[4]谢识予.经济博弈论 [M].上海:复旦大学出版社,2002:25-32.

[5]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2004:10-16.

[6]尹成杰.粮安天下[M].北京:中国经济出版社,2009:15-17.

[7]张 峰.论博弈逻辑的分析方法——纳什均衡分析法 [J].北京理工大学学报 (社会科学版),2008,(2):10-12.

[8]李保明,刘家壮.效用函数与纳什均衡[J].经济数学,2000,17(4):21-28.

[9]龙 方.新世纪中国粮食安全问题研究[M].北京:中国经济出版社,2007:200-235.