潜艇操纵性多目标优化及灵敏度分析

2011-04-20钱家昌

船舶力学 2011年7期

钱家昌，刘卉

（1武汉第二船舶设计研究所，武汉430064；2中国舰船研究院，北京100192）

1 引言

潜艇操纵性能设计是一个典型的多目标优化问题，涉及到潜艇主尺度，潜艇附体（包括有围壳、围壳舵、艉水平翼和艉垂直翼等）的尺度和相对位置等多个设计变量，在满足工程设计约束的同时，追求潜艇操纵性能更优。

多目标遗传算法（MOGAs）是一种常用的多目标优化算法。适合求解带有多参数、多变量、多目标优化问题，具有全局性优化的特点，是近年来迅速发展的一种算法，如向量评估遗传算法（Vector E-valuated Genetic Algorithm，VEGA[1]）、非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm，NSGA[2]、NSGA-II[3]）、强度Pareto进化算法（Strength Pareto Evolutionary Algorithm，SPEA[4]、SPEA2[5]）、相邻繁殖遗传算法（Neighborhood cultivation genetic algorithm，NCGA[6]）等。VEGA[7]对目标函数处理比较简单，找到的解大多属于Pareto前沿的始末端处，产生不了前沿上均匀分布的解结果，并且当搜索空间非凸时无法求得Pareto解；NSGA、NSGA-II利用非支配排序机制，可以很好地搜索非劣解区域，其搜索性能与共享参数的选择密切相关，该方法应用于许多研究领域，比如：UAV的概念设计[8]、结构拓扑优化[9]、潜艇耐压柱壳优化设计[10]等；NCGA算法在SPEA2算法的基础上对种群中个体的交叉操作新增了“相邻繁殖”（Neighborhood Cultivation）机制，在处理多峰和多设计参数问题时比NSGA II和SPEA2更有优势，能够加速收敛进程，具有寻优效率高，可行解分布范围广、过渡光滑等特点。该方法应用于超燃冲压发动机部件优化[11]、火炮结构设计和分析[12-13]和水轮机叶栅设计[14]等诸多方面。

在船舶工程领域，遗传算法（Genetic Algorithm，GA）得到了越来越广泛的应用，主要有：船舶方案设计[15-18]，主尺度优选[19-20]，舱室优化布置[21-22]，隔振系统设计[23]，结构设计[24-25]，坐墩设计[26]和船舶浮态设计[27]等，以及船舶设计建造其他方面[28-30]。但是对于潜艇操纵性的多目标优化及灵敏度分析方面的研究较少。

本文以潜艇操纵性为研究对象，将潜艇操纵面的几何尺度和纵向位置作为设计变量，建立潜艇操纵性指标预报数学模型，采用NCGA遗传算法对潜艇操纵性指标进行多目标优化设计，并进一步开展潜艇操纵性指标的灵敏度分析，评估操纵面参数对操纵性指标的影响。

2 潜艇操纵性指标

潜艇操纵性指标很多，本文只考虑了如下潜艇操纵性指标参数：垂直面内的静不稳定系数la′、垂直面内的动稳定系数Kvd、艉升降舵逆速Uis、围壳舵速升率Uδb、艉升降舵速升率Uδs、水平面内的动稳定系数Khd以及潜艇的相对回转半径Ro。对潜艇操纵性指标的计算主要分为以下两个方面。

2.1 潜艇水动力系数估算

潜艇水动力系数的估算可归结为对主艇体和艇体附体水动力系数的估算，参照国家标准分别估算得到主艇体以及艇体附体归一化后的一次项无因次水动力系数，包括横向力系数、垂向力系数、转艏力矩系数以及纵倾力矩系数等。并将整艇的水动力系数考虑为主艇体以及各部分附体的线性叠加：

式中：F为潜艇整艇水动力系数；FH为主艇体水动力系数；FF为附体水动力系数。

本文暂不考虑螺旋桨对潜艇水动力的影响并基于母型艇试验数据对估算的水动力系数进行修正，利用公式（2）得到设计艇最终的各部分线性水动力系数值：

式中：Fj-d′表示设计艇的线性水动力系数；Fj-d.c′表示设计艇用上述方法计算得到的线性水动力系数；Fj-o.c′表示母型艇用上述方法计算得到的线性水动力系数；Fj-o.t′表示母型艇通过模型试验得到的线性水动力系数。

2.2 潜艇操纵性指标计算

潜艇操纵性指标按照参考文献[31-34]中的公式计算，公式中各项的意义同文献[31-34]。

其中的非线性二次项无因次水动力系数采用母型艇的模型试验值。求解方程（9）得到水下定常回转运动的潜艇相对回转半径为：

3 潜艇操纵性多目标优化及灵敏度分析问题的描述

3.1 潜艇操纵性多目标优化问题的描述

潜艇操纵性是典型的多目标优化设计问题，其数学优化问题可描述为以潜艇操纵面几何尺度和纵向位置为设计变量，在满足工程设计规范等约束条件下，通过优化设计获得潜艇操纵性指标的Pareto最优解集。

（1）设计变量

假设潜艇主艇体参数以母型值为基础不变，选择潜艇操纵面附体尺寸及附体纵向坐标作为设计变量有：

1）指挥室围壳

指挥室围壳高Hfw，指挥室围壳弦长Lfw，指挥室围壳纵向坐标Xfw。

2）围壳舵

围壳舵展长bofws，围壳舵平均弦长Cfws，围壳舵纵坐标Xfws，围壳舵处壳体平均厚度Dhfws。

3）艉水平翼

艉水平翼翼展bohf，艉水平翼平均弦长Chf，艉水平翼纵坐标Xhf。

4）艉垂直翼

艉垂直翼翼展bovf，艉垂直翼平均弦长Cvf，艉垂直翼纵坐标Xvf。

其中：以母型艇船舯为坐标原点按照艇体坐标系计算附体纵坐标值，各设计变量的取值范围综合考虑指挥室围壳内升降装置的高度限制，艉水平翼翼展不宜超宽等工程设计条件。

（2）约束条件

依据行业标准和规范，潜艇操纵性指标的约束条件选择如下：

c1≤la′≤c2;c3≤Kvd;c4≤Khd;Ro≤c5

其中设计参数取值范围根据国家标准确定。

（3）目标函数

在满足约束条件的情况下，潜艇操纵性指标在设计空间内有一定的设计偏好，本文追求潜艇操纵性指标Kvd、Khd、Uδb、Uδs尽量大，la′、Uis、Ro尽量小。则潜艇操纵性多目标优化问题可表示为：

（4）优化方法

本文采用NCGA对潜艇操纵性进行多目标优化分析。NCGA是近年来兴起的一种多目标遗传算法，其对简单遗传算法的改进主要在于交叉、变异算子。NCGA交叉算子中的两个相互交叉的个体不是随机选择的，而是选择两个比较接近的个体。这样可以使交叉后产生的子个体较为接近父代个体，通过排序后分组进行交叉的方法实现“相邻繁殖”机制，从而使接近于Pareto前沿的解进行交叉繁殖的概率增大，加快收敛速度。在加速收敛的过程上比传统遗传算法存在明显的优势。

NCGA算法按以下步骤进行：

1）初始化：令k＝0，设置第一代个体P0，种群数N。计算个体对应的适应度，计入A0；

2）令t=t+1，Pt=At-1；

3）排序：个体按向聚集的目标值的方向进行排序；

4）分组：个体Pt根据排序分成若干组，每组由两个个体组成；

5）交叉和变异：在每一组中执行交叉和变异操作，由两个父代个体产生两个子代个体，同时父代个体被删除；

6）重组：所有子代个体组成一组新的Pt；

7）更新：将At-1与Pt组合，按环境选择机制，从2N个个体中，选出其中N个个体；

8）返回2）或终止。

3.2 潜艇操纵性灵敏度分析问题的描述

在实际工程设计中，获得一个问题的最优解并不一定是最终目的，更深入地分析设计变量对设计指标的影响变化具有积极的现实意义，这就需要对设计问题开展灵敏度研究。

灵敏度是指标对某些参数的变化梯度，本文定义为：

式中：ui为潜艇操纵性指标；xj为潜艇操纵性设计变量。

4 潜艇操纵性多目标优化及灵敏度分析结果

4.1 潜艇操纵性多目标优化

在iSIGHT优化平台下实现对潜艇操纵性数学模型的集成优化分析，其中潜艇操纵性优化数学模型采用Matlab软件编程完成，NCGA算法的参数设置如表1所示。

表1 NCGA参数设置Tab.1 Parameters setting for NCGA

总的计算次数为2 600次，得到可行解2 320个，其中Pareto解52个，上述计算采用配置为Intel Core2 E8300处理器，4GB内存的计算机耗时10分钟完成。

给出优化设计Pareto解集中围壳舵速升率Uδb和艉升降舵速升率Uδs两目标优化结果的二维散点图，见图1。

图1中的优化方案1和优化方案2是从52个Pareto解集中提取在Uis、Uδs、Uδb和Ro四个操纵性指标上均比初始方案要优的设计结果，其相对初始值的改进程度见表2。

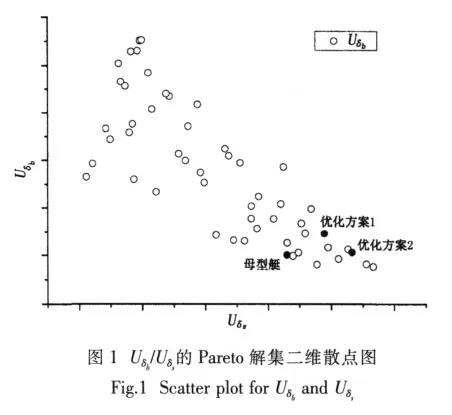
表2 优化方案与初始方案对比Tab.2 Comparision between the optimized results and the initial case

可以看出，优化方案相比初始方案而言，在操纵性指标上均有一定程度的改进，达到了对初始方案的优化设计的目的。

4.2 潜艇操纵性指标灵敏度分析

在iSIGHT平台下进一步对七个潜艇操纵性指标进行灵敏度分析。

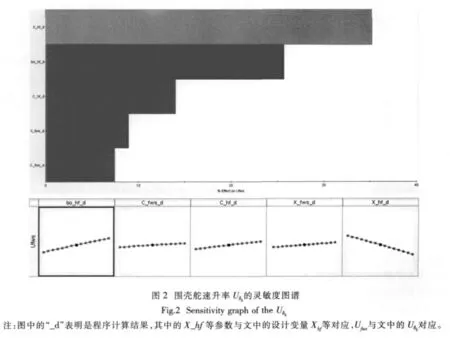
以围壳舵速升率Uδb（对应于图中的Ufws）的灵敏度为例，图2给出了对Uδb影响最大的前五个设计变量的灵敏度大小，并以颜色和趋势区分正负效应。可以看出，艉水平翼的纵向位置Xhf、翼展bovf、平均弦长Chf对其速升率影响较大，同时，围壳舵的纵向位置Xfws和平均弦长Cfws也有一定影响；另外，艉水平翼纵向位置Xhf对Uδb的影响趋势与其它设计参数相反。

整理得到潜艇操纵性指标的灵敏度分析结果，见表3。

表3 设计指标灵敏度分析Tab.3 Sensitivity analysis of the design objects

从图2和表3的结果分析表明：

（1）艉水平翼纵向位置Xhf对垂直面静不稳定系数la′、垂直面动稳定系数Kvd和围壳舵速升率Uδb的影响最大，la′随着Xhf的增大而增大，但是Kvd和Uδb随着Xhf的增大而减小。艉水平翼的几何尺寸bohf、Chf也对该操纵性指标有较大影响。

（2）围壳舵平均弦长Cfws对围壳舵逆速Uis影响最大，Uis随着Cfws的增大而减小。围壳舵逆速Uis还受围壳舵翼展bofws和艉水平翼纵向位置Xhf的影响。

（3）艉水平翼翼展bohf对艉升降舵速升率Uδs影响最大，Uδs随着bohf的增大而减小。其纵向位置Xhf和平均弦长Chf也对Uδs有较大影响。

（4）艉垂直翼设计参数对水平面动稳定系数Khd和相对回转半径Ro的影响最大。其中纵向位置Xvf对Khd影响最大，Khd随着Xvf的增大而减小；平均弦长Cvf对Ro影响最大，Ro随着Cvf的增大而增大。

这些结论与文献[35]相符，而且本文还考虑了艉水平翼纵向位置Xhf和艉垂直翼纵向位置Xvf等多个操纵面参数对潜艇操纵性指标的灵敏度影响，可为设计人员提供更多的设计参考。

4 结论

本文以潜艇操纵面的几何尺度和纵向位置为设计变量，建立潜艇操纵性指标预报数学模型，利用iSIGHT优化软件，采取NCGA遗传算法开展多目标优化设计，并进行了灵敏度分析，得到的主要结论为：

（1）相邻繁殖遗传算法（NCGA）能够很好地处理潜艇操纵性多目标优化问题，在iSIGHT平台下开展潜艇操纵性多目标优化设计能够快速获得Pareto非劣解集，为工程设计提供更多的方案选择。

（2）艉水平翼操纵面参数对垂直面静不稳定系数、垂直面动稳定系数、艉升降舵速升率和围壳舵速升率影响最为强烈；

（3）围壳舵几何参数对围壳舵逆速的影响居于首要地位；

（4）艉垂直翼操纵面参数对水平面动稳定系数和相对回转半径的影响最大。

（5）潜艇操纵面设计参数对操纵性指标的影响有程度大小和正负效应之分，相关设计结果能够为工程设计以及改进工作提供参考。

本文所采用的潜艇操纵性设计方法主要来自于相关的设计规范和经验估算公式，在潜艇操纵性数学模型的精度上还有待改善，仅适用于潜艇设计的初期，因此还需要开展更深入的工作：

（1）结合工程实际，综合运用多种手段，比如引入CAE仿真分析，建立更加精确的计算模型。

（2）面对更加复杂的问题，需要综合考虑设计中涉及的其它学科知识，开展多学科的设计优化（MDO）研究也是发展的一个重要方向。

[1]Schaffer J D.Multiple objective optimization with vector evaluated genetic algorithms[C].Proceedings of an International Conference on Genetic Algorithms and Their Application,1985.

[2]Srinivas N,Deb K.Multiobjective optimization using nondominated sorting in genetic algorithms[J].Evolutionary Computation,1994,2(3):221-248.

[3]Deb K,Agrawal S,Pratap A,Meyarivan T.A fast and elitist multiobjective genetic algorithm:NSGA II[J].IEEE Transaction and Evolutionary Computation,2002,6(2):182-197.

[4]Zitzler E,Thiele L.Multiobjective evolutionary algorithm:A comparative case study and the strength pareto approach[J].IEEE Transaction on Evolutionary Computation,1999,3(4):257-271.

[5]Zitzler E,Laumanns M,Thiele L.SPEA2:Improving the performance of the strength pareto evolutionary algorithm[R].In Technical Report 103,Computer Engineering and Communication Networks Lab(TIK),Swiss Federal Institute of Technology(ETH)Zurich,2001.

[6]Shinya W,Tomolyuki H,Mitsunori M.Neighborhood cultivation genetic algorithm for multi-objective optimization problems[C].Proceedings of the 4th Asia-Pacific Conference on Simulated Evolution and Learning(SEAL-2002),2002:198-202.

[7]崔逊学.多目标进化算法及其应用[M].北京:国防工业出版社,2008:51-52.

[8]Rajagopal S,Ranjan Ganguli A C R Pillai,Lurdharaj A.Conceputual design of medium altitude long endurance UAV using multiobjective genetic algorithm[C]//48th AIAA/ASME/ASCE/AHS/ASC structures,structural dynamics,and meterials conference.Honolulu,Hawaii,2007.

[9]Rhodes O,Santer M.Optimal problem definition for optimization of morphing structures[C]//51th AIAA/ASME/ASCE/AHS/ASC structures,structural dynamics,and meterials conference.Orlando,Florida,2010.

[10]李学斌,朱学康.潜艇耐压圆柱壳的多目标优化设计[J].中国造船,2009,50(1):10-18.

[11]陈兵.空间推进算法及超燃冲压发动机部件优化设计研究[D].北京:北京航空航天大学,2006.

[12]龚海岳.牵引火炮总体结构多目标优化研究[D].南京:南京理工大学,2006.

[13]柳高洁.自行火炮结构动力学分析及优化设计研究[D].南京:南京理工大学,2009.

[14]朱国俊,罗兴锜,郭鹏程,戴辰辰.基于组合优化方法的平面叶栅优化设计[J].大电机技术,2010(1):50-53.

[15]Skinner B A,Palmer P R,Parks G T.Multi-objective design optimization of submarine electric drive systems[J].IEEE,1-4244-0947-0/07,2007.

[16]Christopher R.Blizzard,Kyle Colantonio,et al.Design report of ballistic missile defense submarine[R].Virginia Tech:O-cean Engineering Design Project AOE 4066,2008.

[17]Rahul V.Shinde.An automated multidisciplinary design optimization method for multi-hull vessels[D].Masters Degree of Science in Mechanical Engineering,University of Pune.2007,4.

[18]李学斌,潘治.潜艇概念设计阶段的多目标优化研究[J].海军工程大学学报,2008(2):56-60.

[19]柳存根,裘泳铭,姚震球等.遗传进化算法在船舶初步设计中的应用[J].上海交通大学学报,2000,34(1):41-45.

[20]李文龙,谭家华.集装箱船主尺度全局最优化的混沌算法[J].中国造船,2003,44(1):11-16.

[21]李俊华,陈宾康,应文烨,秦汝平.CADDS5平台上基于遗传算法的船舶舱室优化布置[J].中国造船,2001,42(1):1-5.

[22]张国忠,刘玉君.基于遗传算法的机舱三维优化布置设计[J].造船技术,2005(6):17-19.

[23]毛为民,伍先俊,朱石坚.遗传算法在船舶动力机械混合隔振系统优化设计中的应用[J].中国造船,2005(4):19-25.

[24]李仲伟,吴有生,崔维成.基于有限元法的小水线面双体船结构优化[J].船舶力学,2005,8(2):99-108.

[25]李学斌,朱学康.潜艇耐压圆柱壳的多目标优化设计[J].中国造船,2009(1):11-18.

[26]程远胜,游建军.船舶坐墩墩木布局及尺寸优化设计[J].船舶力学,2004,7(2):63-70.

[27]陆丛红,林焰,纪卓尚.遗传算法在船舶自由浮态计算中的应用[J].上海交通大学学报,2005(5):701-705.

[28]杨启,黄小勇,谭家华,王呈方.基于最优Pareto集的船舶出坞拖轮配置优化[J].中国造船,2005(6):69-74.

[29]周玉龙,杨松林,奚炜等.基于遗传—混沌算法的船舶动力学性能综合优化研究[J].舰船科学技术,2005(4):18-21.