锥管中流动工作介质的声传递特性研究

堵 锋，孙玉东，钟 荣

（1军代表室，江苏 无锡 214061；2中国船舶科学研究中心，江苏 无锡 214082）

1 引 言

锥管是船舶管路系统中不同管径管路之间的过渡元件，与直管不同，经过该元件时同时产生平均流速和声传递特性的变化。为应用传递矩阵法对整个管路系统进行声学分析，必须对组成系统的典型元件之一—锥管建立适当的理论模型，并进行流速和锥角等参数对声传递特性影响的分析，以指导管路系统的工程设计。

锥管是一种变截面管道。在变截面管道方面，Eisenberg等人（1971）[1]采用线性摄动和变量转换，获得流动管路中解耦的两个线性常微分方程，对特殊形状的半无限扩张管进行求解，表明了变截面管道中的驻波特性和平均流与声之间的能量交换。对低马赫数流动（Ma≤0.2）下的锥管以及沿轴线分别呈指数变化、抛物线变化、双曲线变化的非均匀截面管道中的平面波传播，Easwaran和Munjal（1991，1992）[2-3]给出了传递矩阵的解析解。Miles（1982）[4]对一段扩张—收缩管，采用面积指数变化的多个分段模拟变截面管道，将有解析解的各段传递矩阵连乘获得总传递矩阵，研究有流和无流情况下一维管内声传播的驻波压力和相位角，发现管道通流截面积1/2的变化系数将足以产生较大幅值的声反射。作为变截面管道的分段模拟，每一分段为均匀直管时公式最为简单，但这种离散模拟在分段之间形成了突变。Gupta等人（1995）[5]考虑有流动情况下变截面管道各分段之中流动马赫数及温度差异的影响，对分段直管模拟法进行了修正。Gupta（1995）[6]进一步比较了文献[4-5]两种方法的区别。对无流动、余弦型变截面管道中的声传播，Arenas等人（2000）[7]应用Floquet理论进行了解的稳定性分析，采用匹配近似方法获得反射系数并与WKB近似解比较。

本文研究沿锥管不同截面平均流速变化下的管中声传播特性。由于管道横截面的变化，导致声介质特征阻抗的连续变化而产生附加的声反射和驻波效应。本文推导了锥管声传递矩阵的解析解，并以此为基础，采用无反射终端条件下元件声传递效果的评估公式，给出锥管声传递特性随锥角等参数变化的计算结果。

2 沿轴向平均流速变化锥管的声传递矩阵

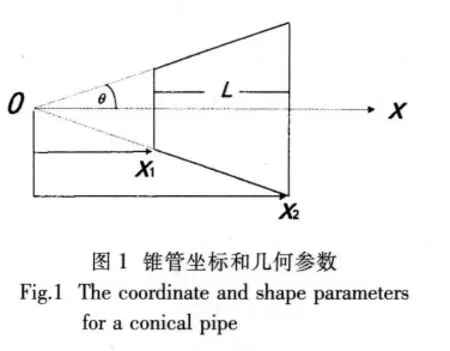
设锥管轴向坐标为x，锥管长度为L，锥角为θ，见图1。

锥管的端部直径分别为：

圆形截面锥管任意截面的横截面面积为：

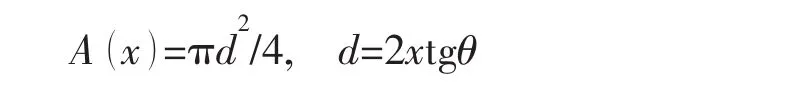
设管中流体为理想无粘，由势函数φ，声压p和质点扰动速度u可表示为：

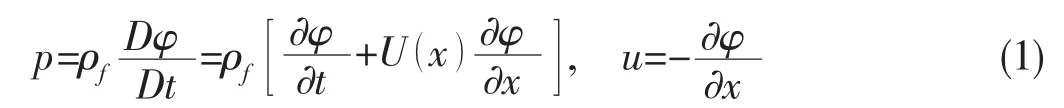
式中ρf为流体介质密度，D/Dt为迁移导数，U（）x为局部平均流速。

令时间因子为 ejωt，φ=fejωt，f满足以下波动方程：

式中M（x）=U（x）/c为局部马赫数，k0=ω/c为静止流体中声传播波数。

解（2）式，得：

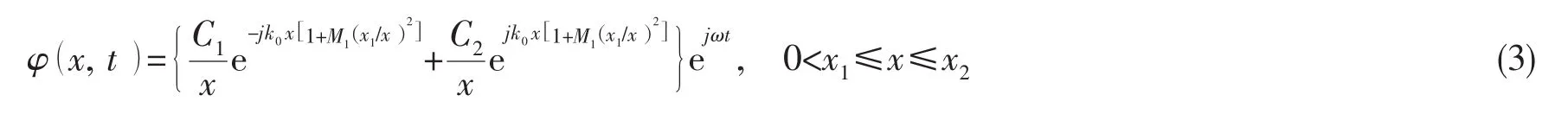
式中M1（x）=U1（x）/c为 x=x1处的局部马赫数，C1、C2为待定常数。

将（3）式代入（1）式，得：

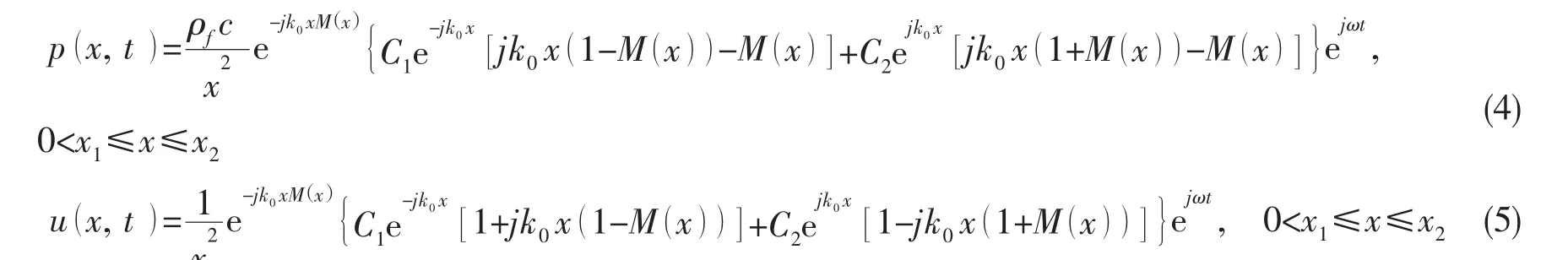
根据脉动流量q（x）=u（x） A（x），采用以下端部条件：

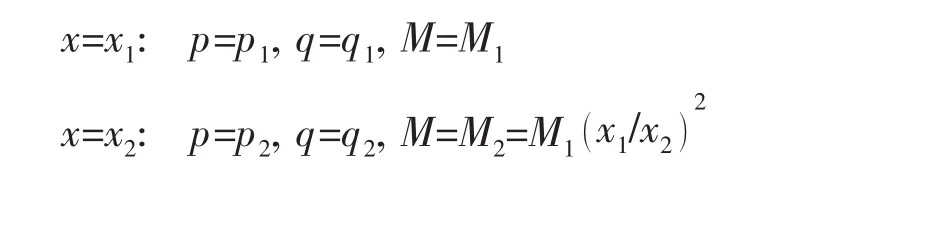
由（4）式和（5）式确定 C1、C2，得锥管传递矩阵 T：

其中：

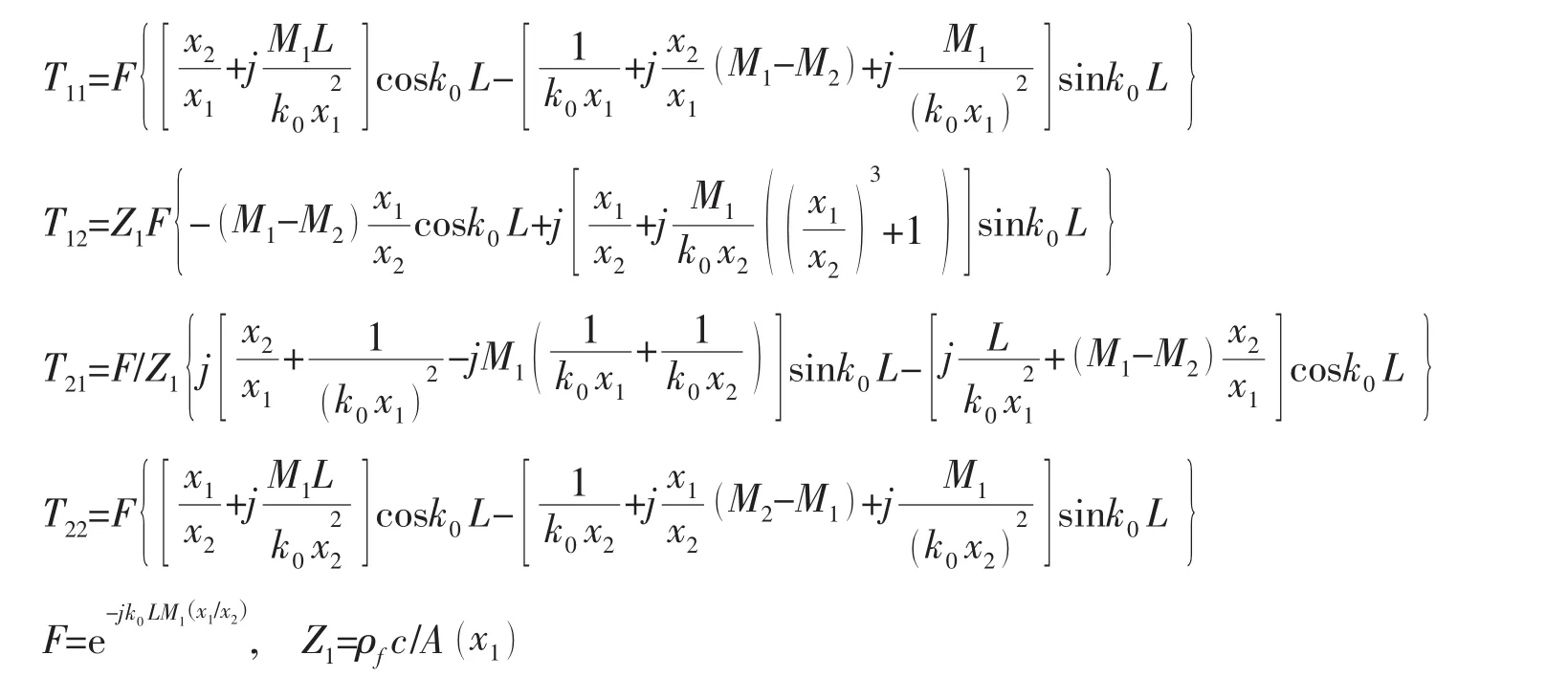
由获得的以上形式的解，可以退化到几种特殊情况：

（1）无流动情况下的锥管：M1=M2=0

（2）不考虑平均流动随轴向变化的锥管：M1=M2≠0

（3） 均匀流动情况下的直管：M1=M2≠0，θ→0，x1，x2→∞

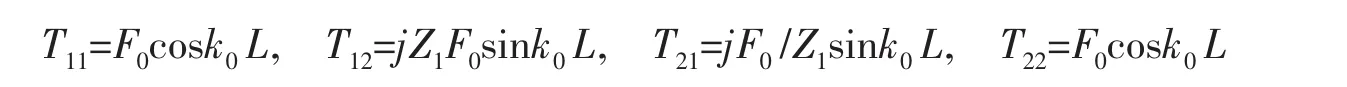
对一般锥管，考虑平均流速沿轴向的变化，进行一定变径比 （d2/d1）下马赫数Mach和锥角θ（相应改变长度L）对锥管声传递矩阵影响的计算。计算结果见图2和图3。计算采用的数据见图2和图3的图题下。 该锥管的变径比 （d2/d1）约为4，在锥角 θ为5°时长度为0.44 m。

以20log10（）表示传递矩阵元素的无量纲结果，其中T11和T22本身为无量纲量，T12、T21以上游端锥管横截面的特征声阻抗Z1无量纲化，分别变为无量纲量T12/Z1、T21×Z1。

图2表示马赫数即平均流速的影响。由图2可见，不同马赫数对T11和T22的影响主要在谷值频率及其幅值。Mach=0.0时锥管中正、反向波频率相同，叠加而产生驻波或共振，在无损耗时共振幅值趋于无穷大，压力比趋于负无穷；Mach≠0.0而逐渐增大时，由于多普勒效应，管中正、反向波频率差异增大，驻波或共振现象减弱，对于T11谷地逐渐消失。不同马赫数对T12的影响主要在低频和谷值频率上，随马赫数增大而增大，而在其它频率上影响不明显。不同马赫数对T21在低频影响很小，在高频的影响也在谷值附近。

图3表示不同锥角θ对传递矩阵中各元素的影响。一定变径比 （d2/d1）下，锥管锥角θ的变化对应于长度L的变化，锥角θ减小时，长度L相应增大，锥管段的轴向声共振频率降低。对T11来说，在小锥角，除了共振频率及附近外，计算频率中频范围的压力比可大于10 dB。T22在整个频率范围内均为负分贝，在大锥角20°时保持在0 dB附近。对T12和T21，小锥角时因共振而起伏变化，但大锥角时均随频率升高而增大并趋于平坦。

3 锥管声传递损失的计算

在理想的声学效果评估中，不考虑管路元件的实际安装环境，即不管自上游到达该元件的声学状态如何，也不考虑元件出口端来自下游的反射，即无反射终端（Anechoic Terminal），计算元件进口端入射声波能量与出口端透射声波能量之比，以传递损失 TL（Transmission Loss）表示。

到达元件端口1的声压p1和脉动流量q1为：

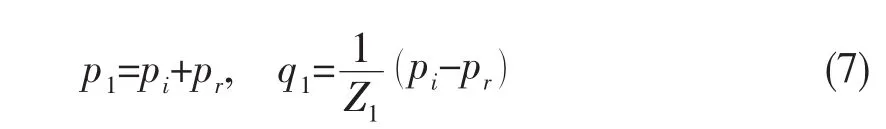
因此有：

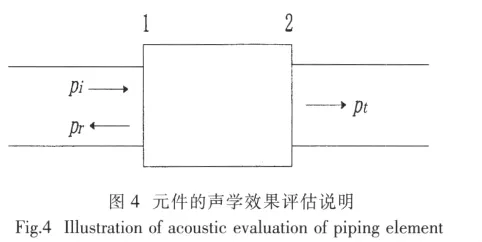
元件端口2有：

以上（7）～（9）诸式中 Z1、Z2分别为进、出口端管路的特征阻抗：Z1=ρfc1/A1，Z2=ρfc2/A2。

采用传递矩阵（6）式和（7）～（9）式，得入射声压分别与透射和反射声压之比为：

以声阻抗矩阵表示时，端口1和2之间有：

入射声压与透射和反射声压之比相应为：

入射波功率Wi、反射波功率Wr和透射波功率Wt与其声压幅值关系为：

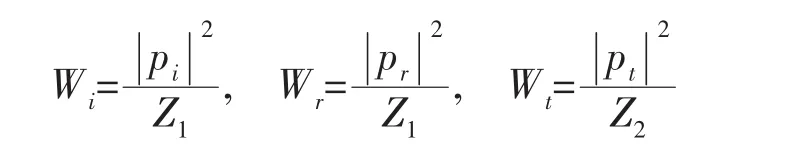
传输损失TL为：

采用第二节中获得的锥管元件的传递矩阵进行计算。对于不同锥角的锥管，传递矩阵计算结果见图3，以此计算锥管所在管路中反射、透射声能与入射声能之比及其总和，见图5。由图中可见，随频率升高，反射声能减小，相应地透射声能增大，而反射、透射声能之和与入射声能比值保持为1。在锥管进、出口管径及变径比一定时，低频的反射系数约为0.8，即透射系数为0.2，但随频率升高，相对于大锥角锥管，小锥角锥管的反射声能较少，透射声能较大。以传递损失表示于图6中，变径比约为4的锥管，低频传递损失最大约为6.8 dB，到高频，小锥角锥管的传递损失逐渐减小，而大锥角（20°）锥管的传递损失仍能达到6 dB。

4 结 论

本文以船舶管路系统中的典型管件之一锥管为对象，考虑平均流速随锥管轴向的变化，推导了声传递矩阵的解析解及特定情况下的简化形式；以一般管路元件的声传递矩阵或阻抗矩阵为输入参数，给出了声传递效果评估的计算公式。

通过算例给出的计算结果，得到以下结论：

（1）虽然船舶管路特别是水管路中流速较低，但由于多普勒频移效应，流速对管路声传递特性还有细微影响，特别在管路声共振的频率附近，会降低共振幅值；

（2）在工程所需要的一定变径比下，增大锥角，即减小锥管长度，将增大声传递损失，对管系降噪有利，但同时会使流动引起的二次噪声增加，因此应综合考虑。

[1]Eisenberg N A，Kao T W.Propagation of sound through a variable-area duct with a steady compressible flow[J].J Acoust.Soc.Am.,1971,49(1):169-176.

[2]Easwaran V,Munjal M L.Plane wave analysis of conical and exponential pipes with incompressible mean flow[J].J Sound and Vibration,1992,152(1):73-93.

[3]Easwaran V,Munjal M L.Transfer matrix modeling of hyperbolic and parabolic ducts with incompressible mean flow[J].J Acoust.Soc.Am.,1991,90(4):2163-2172.

[4]Miles J H.Verification of a one-dimensional analysis of sound propagation in a vriable-area duct without flow[J].J Acoust.Soc.Am.,1982,72(2):621-625.

[5]Gupta V H,Easwaran V,Munjal M L.A modified segmentation approach for analyzing plane wave propagation in non-uniform ducts with mean flow[J].J Sound and Vibration,1995,182(5):697-707.

[6]Gupta V H.A note on three-dimensional effects in segmentation approach for analysis of one-dimensional waves in ducts of varying cross-sectional area[J].J Sound and Vibration,1995,182(2):323-327.

[7]Arenas J P,Crocker M J.Asymptotic solutions for the acoustic wave propagation in a duct with varying cross-section[C]//Seventh International Congress on Sound and Vibration,July,2000.Germany,2000.