移动粒子半隐式法的大涡模拟研究与应用

潘徐杰，张怀新

（上海交通大学 船舶海洋与建筑工程学院，上海200030）

1 引 言

移动粒子半隐式法（MPS）由Koshizuka[1-2]最早于1995年提出的一种用于计算不可压缩流体运动的无网格方法，是一种完全Lagrange的无网格数值方法。MPS通过各代表流体或边界条件粒子的性质来表现出流场的时－空物理特征。在MPS法中，控制方程采用Lagrange形式的Navier-Stokes方程，方程中不出现对流项，每个计算部分为显式和隐式两步，第一步考虑重力与边界条件的影响，对粒子的速度和坐标进行修正，第二步由第一步引起的粒子数密度变化为条件，建立压力Poisson方程，求得压力后对粒子进行第二次修正，使得粒子的数密度回到初始状态，恰好满足了不可压缩条件。在MPS中，控制方程各项由粒子与周围粒子的关系得到，方程通过这种关系进行离散。同传统的网格法比较，MPS由于控制方程中不存在对流项，避免了可能存在的数值耗散；因使用可移动的粒子来代表流体，使得其在大变形自由表面的模拟中能够较为满意地表现出自由表面的形状；并且粒子布置容易性使得该方法在各种复杂边界条件中均能得心应手。

由于MPS广泛的适用性和良好的前景，该方法在被提出后[1-2]已被运用到许多领域中。1999年，Gotoh[3]用MPS法来模拟波浪的传播问题，讨论了挡板在带有固定不可穿透斜面的水槽中突然运动问题以及可穿透斜面的流体粒子运动过程问题、模拟了带有垂直墙的破碎波问题；从2001年至2003年，Sueyoshi[4-6]在海洋工程领域使用MPS法做了一系列的研究。包括溃坝模型、晃荡模型和具有斜坡长底的溃坝模型的模拟[4]，不具有和具有消波板的溃坝模型的模拟[5]，以及具有液舱和不具有液舱的二维浮体在由数值水池模拟出的恶劣海况下的运动[6]，其中还包括了破损情况下的二维浮体运动等等；2004年，Hibi[7]则将重点放在了由MPS法自身引起的压力振荡现象，专门研究解决压力振荡问题，提出了四种不同的方法来缓解压力问题。其中包括新的底部流体粒子压力计算方式、异相异性的核函数、两次的ICCG迭代、以及修改的压力Poisson方程；2005年，Shao[8]使用带有大涡湍流模式的MPS法和SPH法模拟同一个溃坝模型；另外，同年Gotoh[9]用MPS模拟了水跃问题；2007年，Alam[10]使用MPS模拟了楔形体入水问题，对于水面的破碎又分考虑表面张力和不考虑表面张力两种情况；另外，2008年，Sueyoshi[14]使用MPS模拟了甲板上浪问题。

本文使用MPS法，结合Smagorinsky涡粘模型，模拟了半满液箱的横摇晃荡运动。针对由MPS自身引起的压力震荡现象，选择了带权重的面积－时间平均法，将压力震荡现象缓解至可实际接受的范围内；在自由表面判别方法上，针对原方法容易造成非自由表面粒子被误判这一缺陷，提出了一种基于邻居搜索的混合判别方法，该方法在MPS法容易出错的阶段使用邻居搜索，能够准别地判别自由表面并减少误判情况的产生。

2 控制方程

MPS使用Lagrangian形式的Navier-Stokes方程作为控制方程，过滤后的控制方程有如下形式：

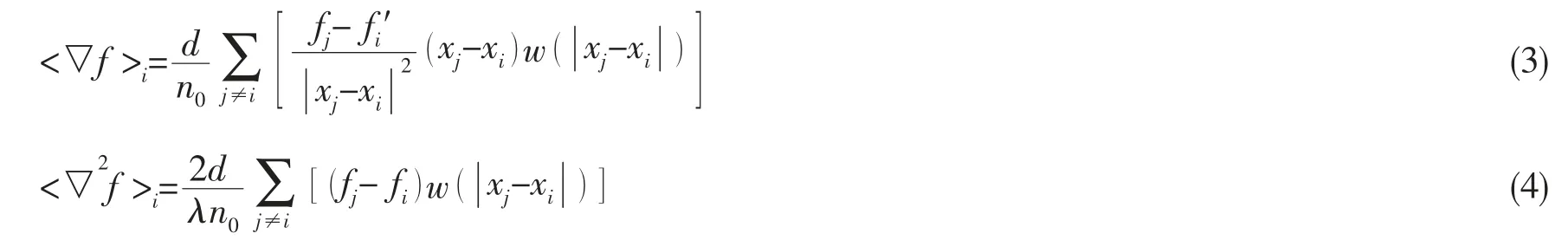
方程（3）是Gradient模型，方程（4）是Laplacian模型，在上述两方程中，d表示空间的维数，n0是初始粒子数密度，矢量xi和矢量xj是粒子i和粒子j的坐标，方程（4）中的λ可由方程（5）求得，粒子数密度n0可由方程（6）求得：

在方程（3）、（4）、（5）和（6）中的w（r）为核函数，可由方程（7）求得：

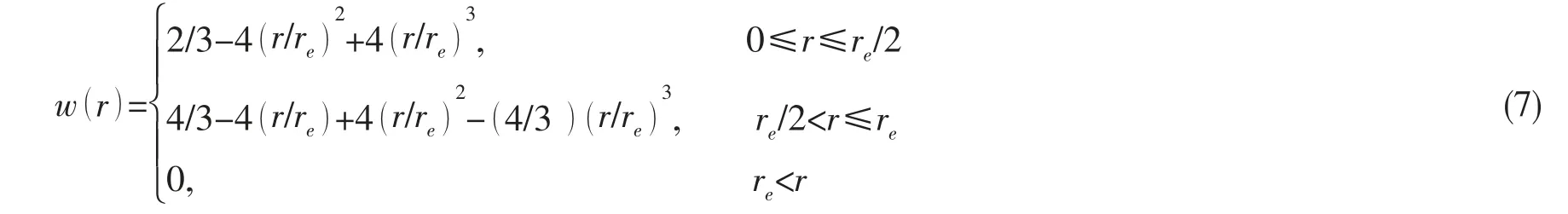
在核函数中，re是核函数的作用距离，r是两粒子间的距离。MPS中的压力，可由压力Poisson方程（8）求得：

将方程（2）中的亚格子应力采用分子粘性形式，可写为：

上式中Cs为Smagorinsky系数，Δ为MPS初始粒子间距。有了上述的方程，MPS法的计算过程可由图1所示。

同一般MPS算法不同的是，考虑大涡模拟的MPS多了亚格子应力需要考虑，亚格子应力同体积力与边界条件一起考虑，如下式所示：

上式中Δui*是中间速度值，Δt为时间增量。而（9）式中的项则并入压力项，同压力泊松方程一同求解，其他过程均同一般的MPS算法一致[13]。

3 基于邻居搜索的混合自由表面判别

原MPS法中使用粒子数密度的变化来识别自由表面，如方程（11）所示：

式中＜n*＞i在某个时间步下的粒子i的数密度，MPS理论推荐β可以选取介于0.8到0.99之间的数。

在MPS模拟中，当粒子处于自由表面处时，粒子周围的邻居较少，所以其数密度也较少，可以方便地识别为自由表面。在MPS的模拟过程中，自由表面的识别是在考虑了体积力和边界条件的第一次粒子速度位置修正后进行的，然后自由表面粒子压力赋0后作为初始条件参与压力泊松方程的求解。MPS理论要求在每一个模拟时间步之后，各粒子的数密度回归为初始粒子数密度，相当于（11）式中数密度参数β为1。但是自由表面的识别在第一次修正之后，粒子的位置发生了变化，也就是参数β值发生了变化，而MPS仅能保证在第二次修正后β值回复为1，所以在自由表面识别的过程中，将有非自由表面的粒子因β值略小而被误判为自由表面粒子，从而压力赋0参与泊松方程的求解，给模拟的结果带来误差，这种情况在流体运动比较剧烈时尤为明显。

本文使用一种基于邻居搜索的自由表面判定方法，邻居搜索区域同Gradient模型方程（3）中的邻居搜索距离一致，那么模拟时就不需要进行额外的邻居搜索工作。考虑到并非只是最表层粒子属于自由表面，实际模拟中靠近表层的粒子都可以作为自由表面处理，所以在邻居搜索时，只考虑粒子周围1.0倍粒子间距到2.1倍粒子间距之间的区域，将该区域分成八分，如有两相邻区域中没有邻居，则认为该粒子属于自由表面，反之则是一般粒子。

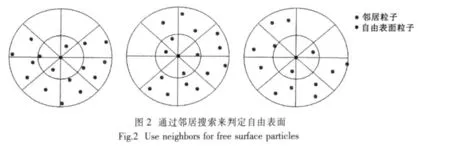
由于对每个粒子进行邻居搜索以判定自由表面较耗费资源，而实际所需要的工作只是要消除因粒子数密度参数略小而被误判的情况发生，所以模拟中进行邻居搜索的对象仅为按方程（11）所选出的粒子。另外，鉴于发生拍击破碎的情况，可能会出现粒子不存在两相邻区域中没有邻居但确实属于自由表面的情形，可将粒子的数密度要明显小于一般粒子的直接归并为自由表面。所以在使用邻居搜索法时，只需要对部分粒子进行识别，这些粒子数密度条件可满足以下条件：

式中A为粒子数密度判定下限，由于这种自由表面判别方式结合传统的MPS自由表面判别方式和邻居搜索法，所以称为混合自由表面判别法。

4 压力震荡现象与缓解

由于自身算法的原因，MPS中的压力存在震荡现象[11-13]。在这方面，Hibi[7]和Sueyoshi[5]都进行过研究。Sueyoshi对浮体的非线性运动模拟中的压力震荡现象，使用了固定的面积—时间平均方法，缓解压力震荡并取得了很显著的效果。而Hibi的多种方法虽然有一定的效果，但是却在不同程度上复杂化了MPS算法，并且其效果同面积—时间平均方法相比，没有绝对的提高，所以本文采用面积—时间平均方法。而在实际模拟过程中发现，数十倍于压力正常值的压力畸点较为频繁地出现在靠近边界处。这是因为在晃荡的模拟中，边界具有速度，在考虑了边界条件的修正后，边界粒子可能与流体粒子距离过近而导致其数密度过大，从而由方程（8）可看出该粒子的压力值将过大。从而本文使用带权重的压力平均方式，当输出粒子点周围有压力畸点出现时，该平均方式可以一定程度上缓解受压力畸点的影响。

5 MPS的大涡数值模拟

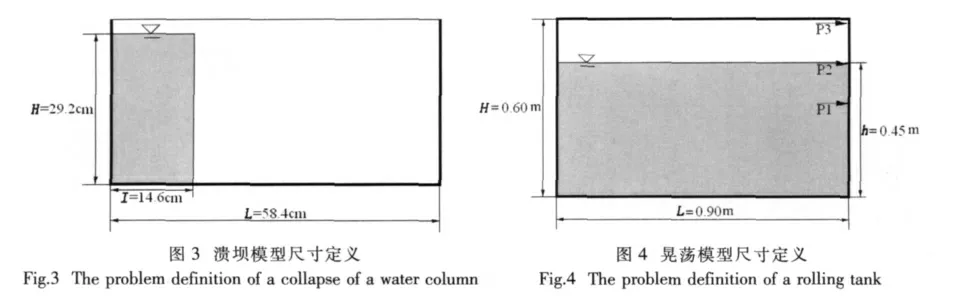
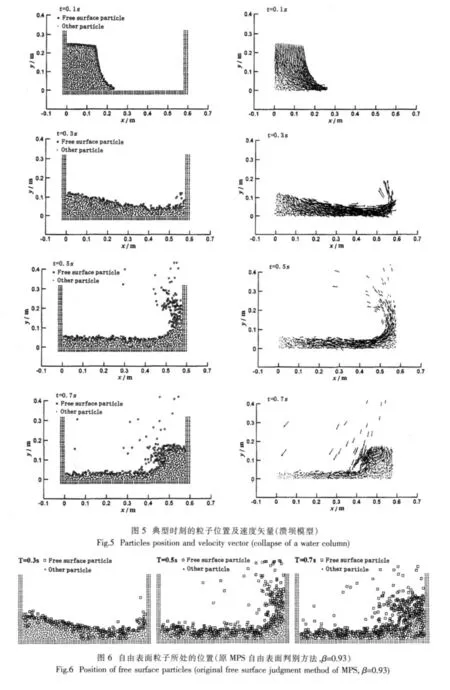
首先选取溃坝模型进行模拟，模型的尺寸如图3所示。在模拟中可以发现，基于邻居搜索的自由表面判定方法能够较为准确地捕捉到自由表面粒子（如图5所示），同原MPS的自由表面判定方法相比（如图6所示），明显地减少了自由表面误判的产生，使用了混合自由表面判定条件的大涡MPS法，能够准确地模拟出溃坝的过程。

接着选取晃荡模型进行模拟，模型尺寸如图4所示，液箱做强迫的横摇正弦运动，其幅度为4°，横摇的频率为0.89Hz，横摇的中心位于舱底中心。而模拟中的三个压力输出值分别放置于左壁的1/2高处、3/4高处与左壁顶部。从模拟结果可以看出，使用了混合自由表面判定条件后，模拟运行顺利，混合自由表面判定方法能够准确地捕捉自由表面粒子。由于在模拟中，除了使用混合自由表面判定条件外，还使用了区域限定。根据文献[12]的研究结果，可以大约估算出自由表面将会出现的位置，对自由表面不会出现的位置划为限定区域，对这部分区域里面的粒子不进行自由表面判定而直接认定为属于非自由表面粒子，这样做不但再次减小了非自由表面粒子被误判的可能性，而且只对部分粒子进行自由表面判定，还增加了模拟的效率，在本次模拟中，被限定的区域设置在液箱的半高以下。从模拟的结果上看，不多的自由表面误判情况都集中在较靠近自由表面附近的区域，而在液箱中部和底部始终没有误判产生，如图7所示，由于晃荡模型中的液位较溃坝模型相比要深，可能会有偶尔的非自由表面粒子被误判为自由表面的情况出现在液箱底部的情形，但使用了区域限制之后，则不会出现这种情况。在模拟的（1/4）T和（3/4）T时，液舱中的液体发生拍击现象，与实验结论一致[13]。当左壁顶部发生拍击时，左壁各压力点处的压力均处于峰值，与拍击基本处于同一时刻，这一点也与实验结论一致[13]。从图7中可以看出，MPS在模拟自由表面的运动方面，有着出色的表现。模拟的压力结果采用面积－时间平均法进行处理，面积为压力输出点同临近点按方程（13）进行，其中n在本文取值为5，在时间平均中，时间段越长，效果则越好[12]，但是过长的时间可能将别的时段的压力平均进来并影响结果，所以本文选取时间段为0.012秒，约等于本文模拟周期1.1236秒的1%。从图8可以看出，平均后的压力无论在表现规律和极值上，都同实验值保持基本一致[13]。

6 结 论

本文使用结合Smagorinsky涡粘模型的大涡移动粒子半隐式法模拟了水柱溃坝过程和液箱横摇晃荡过程。针对原MPS法在模拟中普遍存在的非自由表面粒子被误判为自由表面情况，提出了一种混合自由表面判别法；针对MPS法的压力震荡现象，使用了面积－时间平均法进行处理。从模拟的结果中可以看出，混合自由表面判定条件能够很好地工作，在模拟中对被误判的非自由表面粒子修正的效果明显，基于面积－时间平均的压力震荡缓解方法效果明显，可以将压力震荡现象缓解到工程实际的运用范畴，另外上述方法同基于大涡模拟的MPS法配合良好，模拟顺利，并且其在模拟自由表面的运动方面，与传统的网格比更加方便，并且表现也更加出色。

[1]Koshizuka S,Tamako H,Oka Y.A particle method for incompressible viscous flow with fluid fragmentation[J].Journal of Computational Fluid Dynamics,1995,4:29-46.

[2]Koshizuka S,Oka Y.Moving-Particle Semi-implicit Method for fragmentation of incompressible fluid[J].Nuclear Science and Engineering,1996,123:421-434.

[3]Gotoh H,Sakai T.Largrangian simulation of breaking waves using particle method[J].Coast Engineering Journal,1999,41:303-326.

[4]Sueyoshi M,Naito S.A study of nonlinear fluid phenomena with particle method(Part1)[J].Journal of Kansai Society Naval Architects,2001,236:191-198.(in Japanese)

[5]Sueyoshi M,Naito S.A study of nonlinear fluid phenomena with particle method(Part2)[J].Journal of Kansai Society Naval Architects,2002,237:181-186.(in Japanese)

[6]Sueyoshi M,Naito S.A study of nonlinear fluid phenomena with particle method(Part3)[J].Journal of Kansai Society Naval Architects,2003,239:81-86.(in Japanese)

[7]Hibi S,Yabushita K.A study on reduction of unusual pressure fluctuation of MPS method[J].Journal of Kansai Society Naval Architects,2004,241:125-131.(in Japanese)

[8]Shao S D,Gotoh H.Turbulence particle models for tracking free surfaces[J].Journal of Hydraulic Research,2005,43:276-289.

[9]Gotoh H,et al.Lagrangian particle method for simulation of wave overtopping on a vertical seawall[J].Coastal Engineering Journal,2005,47:157-181.

[10]Alam A,Kai H,Suzuki K.Two-dimensional numerical simulation of water splash phenomena with and without surface tension[J].Journal of Marine Science and Technology,2007,12:59-71.

[11]Pan X J,Zhang H X,Lu Y T.Moving-Particle Semi-implicit Method for vortex patterns and roll damping of 2D ship sections[J].China Ocean Engineering,2008,22:399-407.

[12]潘徐杰,张怀新.移动粒子半隐式法晃荡模拟中的压力震荡现象研究[J].水动力学研究与进展,2008,23(4):453-463.Pan X J,Zhang H X.A study on pressure fluctuation in sloshing simulation of Moving-Particle Semi-implicit Method[J].Journal of Hydrodynamic,2008,23(4):453-463.(in Chinese)

[13]潘徐杰,张怀新.用移动粒子半隐式法模拟液舱横摇晃荡现象[J].上海交通大学学报,2008,42(11):1904-1907.Pan X J,Zhang H X.Moving-Partical Semi-implicit Method for simulation of liquid sloshing on roll motion[J].Journal of Shanghai Jiaotong university,2008,42(11):1904-1907.(in Chinese)

[14]Sueyoshi M,Kashiwagi M,Naito S.Numerical simulation of wave-induced nonlinear motions of a two-dimensional floating body by the Moving Particle Semi-implicit Method[J].Journal of Marine Science and Technology,2008,13:85-94.