基于普通数码相机的DLT摄影测量研究
2011-04-18侯凯丁良国李阳
侯凯,丁良国,李阳
(郑州市规划勘测设计研究院,河南郑州 450052)
基于普通数码相机的DLT摄影测量研究
侯凯∗,丁良国,李阳
(郑州市规划勘测设计研究院,河南郑州 450052)
基于普通数码相机的摄影测量方法的相关实验研究,结合DLT模型以及普通数码相机相片畸变模型,编程实现了标志点图像匹配,进行了相关摄影测量数据的计算分析,得出一些有益的结论。
DLT;摄影测量;普通数码相机相片畸变模型
1 引 言
随着科学技术的飞速发展,当今世界正进入数字化时代,摄影测量学已成为摄影测量技术与计算机科学的交叉学科,摄影测量工具也由计算机及其相关的输入输出设备取代了昂贵的光机设备,科研工作者不再受专业设备的制约。我们可以通过一个或多个数码相机对要监测的目标进行连续摄影,实时地将影像传输到计算机中,由计算机自动进行数据处理,然后在显示屏上看到最终所需的数据,并根据这些数据进行施工现场的实时监控[1]。
普通数码相机具有体积小、质量轻、使用方便、灵活性强等特点,特别是性能的大幅度提高,现已被广泛应用于近景摄影测量领域[2]。但普通数码相机是一种非量测用摄影机,存在物镜构像畸变差较大、内方位元素未知且不稳定等特点[3]。因此利用普通数码相机进行摄影测量时,不能直接采用航空摄影测量中的解析方法处理普通数码影像。
本文主要做了基于普通数码相机直接线性变换(DLT)摄影测量实现的具体研究,包括考虑了普通数码相机物镜畸变差影响模型,DLT摄影测量模型。并且编程实现了标志点图像匹配,考虑了普通数码相机物镜畸变影响的DLT摄影测量数据计算。
2 普通数码相机
2.1 普通数码摄影机物镜畸变差改正模型
目前普通数码影像的摄影测量处理方法可分为两种:一种是先对数码相机进行检校,即测定出数码相机的构像畸变系数和内方位元素,然后对像点坐标进行畸变差改正,再利用以往解析方法求解出待定点的物方坐标;另一种是利用直接线性变换解法求解待定点的物方坐标。第一种方法虽然对控制点要求低,所需控制点个数只要超过3个即可,且解算精度高,但需建立精密的平面控制场和三维控制场。对于一般工程应用,处于条件所限,难以建立精密控制场,对测定精度要求不高的情况,则通常采用第二种方法[4]。
考虑普通数码摄影机物镜畸变差的影响,并引入相应的物镜畸变差改正模型。具体如下:

其中:△x、△y为畸变差改正项;
x0、y0为该相片像主点的像平面坐标;
K1为对称性物镜畸变的待定系数;
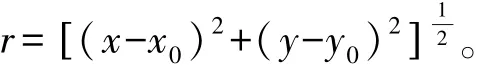
2.2 DLT模型
建立在共线条件基础上的近景解析摄影测量法由于其结算方便、瞬时获取、长久保存、反复使用等特点,在实践中不断得到应用。但是其对摄影机要求较高,
直接线性变换算法是直接建立像平面坐标与物空坐标的关系式的一种解法。计算中不需内方位元素数据(摄影机不需设置框标),也不需要外方位元素的近似值。鉴于在近景摄影测量中越来越广泛地使用各种类型的非量测用摄影机(如普通数码相机),所以直接线性变换算法已成为近景摄影测量的主要结算方法之一。其原理公式是:

其中,x、y为像对平面坐标,X、Y、Z为相片标志点对应的物空坐标。L1~L11为待定系数。
2.3 误差方程
考虑对非量测摄影机物镜畸变差的影响,在上式中加入物镜畸变差改正,则有:

并且可以反算像主点的坐标:
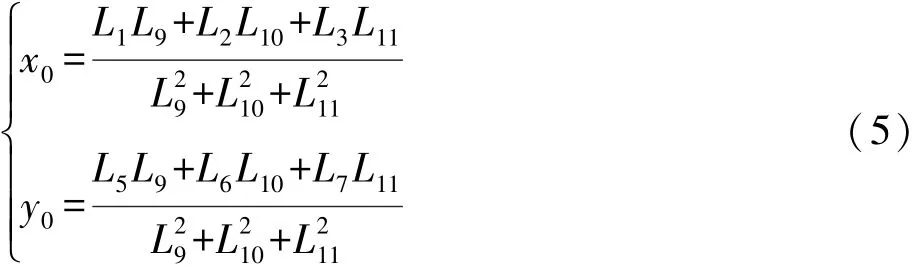
直接线性变换公式是一组非线性公式,它是按迭代法进行最小二乘解算的。解算分为两步,即正算求L系数,反算解求物方待定点的空间坐标。方程式为:

正算的误差方程式:
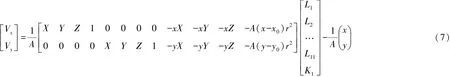
上式简化为:

法方程为:

其解为:
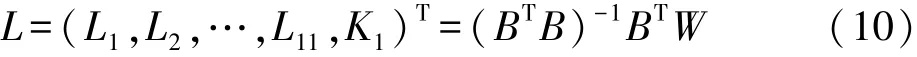
此运算步骤是一个迭代过程,设定一个限制,每次有解得的L值计算A系数,并将解算的A系数再次带入误差方程式计算L系数,如此循环直至小于设置限制为止。
在解求K1之后,便可求得像点改正了畸变差的像平面坐标:

由于各张像片有各自的L系数,以上正算过程应逐片进行。反算的误差方程式:
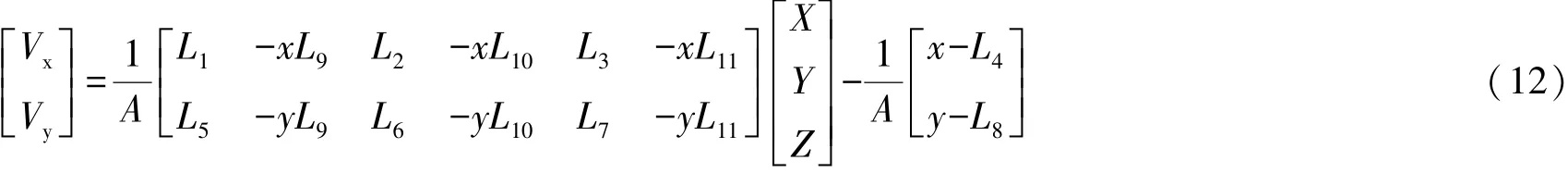
对于每张像片的每一个像点均可列一组式(12),为了求得X、Y、Z三个未知数,则至少需要两张像片(由其上的两个同名像点解算)。其式为:

其解为:

3 实现过程
3.1 标志点图像程序匹配
所谓图像匹配就是把两个不同的传感器从同一景物录取的两幅图像在空间上进行对准,以确定两幅图像之间的平移以及旋转关系[5]。
利用普通数码相机分别从不同位置拍摄的相片,并利用相关摄影测量软件,对每张相片中的各个像点的像平面坐标进行量测。
3.2 顾及普通数码相片对称性物镜畸变差的DLT算法程序实现
利用Visual C++与Matlab接口进行顾及普通数码相片对称性物镜畸变差的DLT算法程序实现,通过前面得到像点平面坐标值数据进行相关的程序实现。具体流程如图1所示。
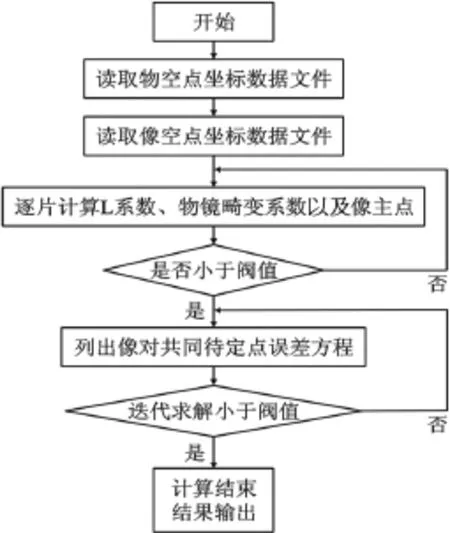
图1 程序流程图
4 试验数据计算和结论
4.1 试验计算
本次摄影测量实验是在室内进行的,在空间内均匀分布若干控制点,控制点分布范围约10 m,Leica TDA 5005工业全站仪通过后方交会的形式得到全部点的坐标值。并用普通数码相机(Sony w130)从不同角度对所有控制点进行摄像。

相片的系数L表1
根据前面的介绍进行程序的计算,其具体结果如表1、表2所示。

相片的系数L(单位/m) 表2
4.2 结论
本文在直接线性变换理论的基础上,考虑普通数码相机对称性物镜畸变差影像模型,同时利用VC++与Matlab接口技术编程实现了解算过程的自动化,在一定程度上提高了精度,通过实验数据的计算分析足以证明该方法的可行性。
以上的数据结果表明,顾及对称性物镜畸变差的DLT摄影测量方法能到毫米级精度。该方法操作简单,程序实现方便,具有一定的现场测量意义。但在试验以及数据计算中,也出现了控制点空间位置分布对解算的影响、相片主点坐标近似值对程序解算的迭代收敛影响等问题都需要进一步的深入的研究和解决。
此外,若在今后的研究中能够使用更高分辨率(有效像素更高)、光学变焦范围更大、光学镜头更好的专业数码相机,则其测量精度会有很大提高。
[1] 于承新,张向东,牟玉枝等.直接线性变换法在变形测量中的应用研究[J].山东建筑工程学院学报,2002.3.(17)
[2] 陈建华,张雷,阮善发.非量测相机同步摄影控制器[J].南京工业大学学报:自然科学版,2003,25(5):92~94
[3] 于君明,黄小波.基于数码相机立体像对的物体三维信息快速获取方法[J].测绘学院学报,2002,19(4):276~279
[4] 苍桂华,林君健,高俊强.广义光束法在普通数码影像中的应用[J].南京工业大学学报,2007,29(6):33~36
[5] 章毓晋.图像工程[M].北京:清华大学出版社,2000
The Research on Photogrammetry of Direct Linear Transformation Based on Common Digital Photos
Hou Kai,Ding LiangGuo,Li Yang
(Zhengzhou Urban Planning Design and Survey Research Institute,Zhengzhou 450052,China)
With the development of science and technology,the use of photogrammetry has been expanding rapidly. This paper has done some experimental research of photography based on the ordinary digital camera.Combined with DLT model and the ordinary digital camera photograph distortion model,this paper carried on the program to realize,then make a calculation analysis of the relevant photographic data and some significant conclusions are obtained.
DLT;Photogrammetry;Distortion model based on common digital photos
1672-8262(2011)02-105-04
P234.1
B
2010—08—08
侯凯(1984—),男,助理工程师,主要从事城市测量技术工作。
