基于磁法探测理论的钢结构变形监测研究

邱子汉，熊助国，刘向铜，沈宝龙，胡鑫

(东华理工大学，江西抚州 344000)

基于磁法探测理论的钢结构变形监测研究

邱子汉∗，熊助国，刘向铜，沈宝龙，胡鑫

(东华理工大学，江西抚州 344000)

地磁场的稳定性以及钢结构的铁磁性是磁法探测理论应用于钢结构变形监测的客观条件。高精度磁力仪应用和电子计算机技术使磁法探测进入了一个高精度测量和自动化解释阶段。本文利用磁场强度与空间位置关系原理，建立了磁法探测理论在钢结构变形监测中的优化模型。应用积分理论中的剖分方法解决非规则钢结构变形体磁场强度的计算问题。通过对承压变形的长方体钢板进行检测数据正演实验，得出挠度与磁场强度的相关方程，初步探索出剖分次数的大小决定了剖分计算的精度，是对钢结构变形监测方法的一次全新探索。

磁场强度；挠度；非规则钢结构；正演；剖分

1 引 言

从1851年英国伦敦为筹备世界博览会，在海德公园兴建水晶宫(Crystal Palace)开始，钢结构作为一种新型的工程模式，由于其相对廉价，抗震性好，施工快等优势，现在运用越来越广泛。变形监测是工程项目生命周期中不可缺少的部分，变形监测的精确性与时效性关系到工程施工与后期运行的安全。对于钢结构的变形监测，除了传统方法，如水准仪、全站仪[1，2]、近景摄影测量[3，4]、GPS[5]等，还出现了应用测量机器人、三维激光扫描仪[6]、液体静力水准仪[7，8]等高新科技手段的测量方法。不管是传统方法还是新方法都是对几何量的处理，或直接或间接。

磁法探测是物探方法中最古老的一种，从20世纪80年代开始，由于高精度磁力仪的应用和电子计算机技术的迅猛发展，使磁法探测进入了一个高精度测量和自动化解释阶段，主要发展有高精度航空磁测系统；地面磁法探测仪器开始更新换代等，扩大了磁法应用范围[9]。

21世纪计算机、高精度磁力仪、空间定位系统GPS的进一步发展普及，磁法探测在新领域也有了长足的发展[10]，如采用高密度磁法对早期垃圾埋场地进行定量探测的应用；高精度航磁在有害废弃物环境调查和污染源探查中的应用；磁梯度测量在探测战争遗留炸弹分布中的应用[11]。这些磁法探测新应用技术的共同点是被探测物体都可以被磁化，既体现了一般磁法探测快捷、高效、安全的优点，又朝向容材料质量检测和几何量的可定量检测于一体方向发展，本文涉及的钢结构完全符合磁化条件，并有着材质和变形控制的多重检测需求。

一般物探用磁场探测仪的几何解析多满足于较宏观的解释要求，随着俄罗斯TSC－1M－4型千分之一级新型高精度应力集中磁检测仪的出现，使磁法探测技术应用于钢结构变形监测迎来了可喜的前景，使磁法探测技术的相关定位几何量精度有了更好的保障，使其应用于变形监测的可能性大大加强。为此本文对磁法探测在钢结构变形监测中的应用进行探索，从以下三个方面阐述这种方法的可行性:

(1)解释磁法探测理论，优化磁法探测理论在钢结构变形监测中应用的计算模型；

(2)对含预制微小孔洞缺陷的钢板进行磁法正演理论计算，并用TSC－1M－4探测仪进行磁场实测，对比理论与实测磁场分布图，以证明磁法探测对于钢结构微小变化的可发现性，探索符合变形监测级精度要求的可能性；

(3)对不同弯曲变形的钢板进行磁场强度正演理论计算，得出磁场强度与挠度的关系。

2 磁法探测理论

物理学告诉我们一块磁铁所产生的磁场是可以把一根铁钉磁化。由文献[12]可知，我们的周围同样存在一个磁场，而这个磁场99%来自于地磁场。由于地磁场是由地球内部产生的，地球结构的稳定性决定了它也具有稳定性。这就为磁法探测钢结构建立了稳定的客观条件。本文中采用1980年编制的全国地磁图中南昌的磁场参数(Mx＝35 520 nT，Mz＝31 520 nT)。

钢结构体的铁磁性决定了它具有磁导力，由于钢结构建筑体大都使用圆状和块状钢材构成，故本文仅对圆柱体和长方体这两种模型空间外任意一点p(x，y，z)的磁场强度进行分析。

2.1 圆柱体模型空间外任意一点磁场强度[12～14]

地下有一均质均匀磁化直立圆柱体，它的磁化强度M＝Mxx0＋Myy0＋Mzz0，高度为H，半径为a，顶面中心点坐标为(ξ，η，ζ)。求地面任意一点p(x，y，z)(柱体外)的磁场强度。

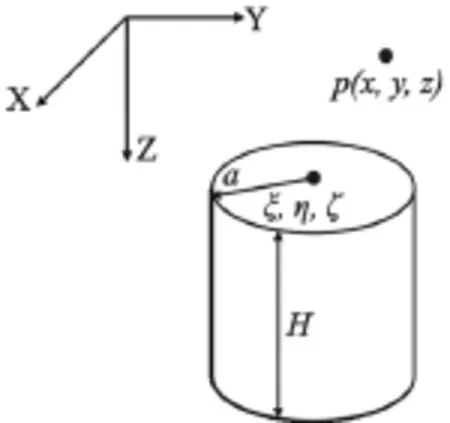
图1 直立圆柱体

解:图1先以圆柱轴的顶面中心为坐标原点O。均质圆柱可近似地视为位于轴上线密度为λ＝πa2ρ的均匀质量线。线元λdz在P点的引力场强度为:

这里:r0是从线元指向测点的单位矢量。

dG可分解为垂直分量dGz为:

我们对其积分得:

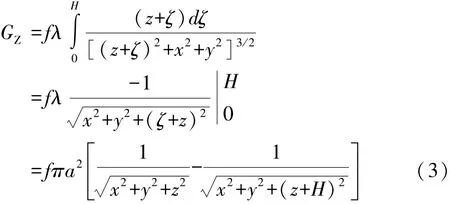
利用泊松公式:

这里:μr为圆柱体的磁导率，Mx，My，Mz为圆柱体的感应磁场强度，x，y，z为P点坐标，H为圆柱体的高度。

2.2 长方体模型空间外任意一点磁场强度[12～14]

设有一X方向为a，Y方向为b，Z为c的长方体，长方体中心位置为(x0，y0，z0)，如图2所示。

图2 长方体

由引力场计算公式可知，P点的引力位为:

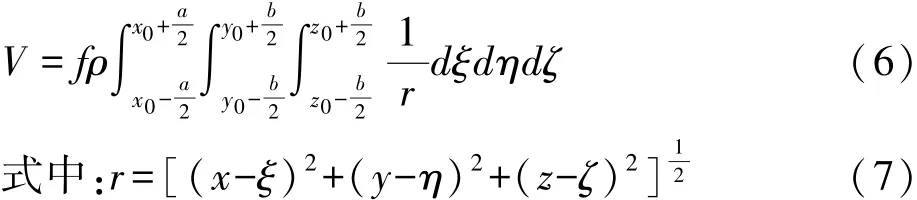
郭志宏等人对上式重新求导数并做无奇点出现的积分得:将以上格式带入泊松公式可知:

对上式Hz来说，我们令

故Hz可以展开为:

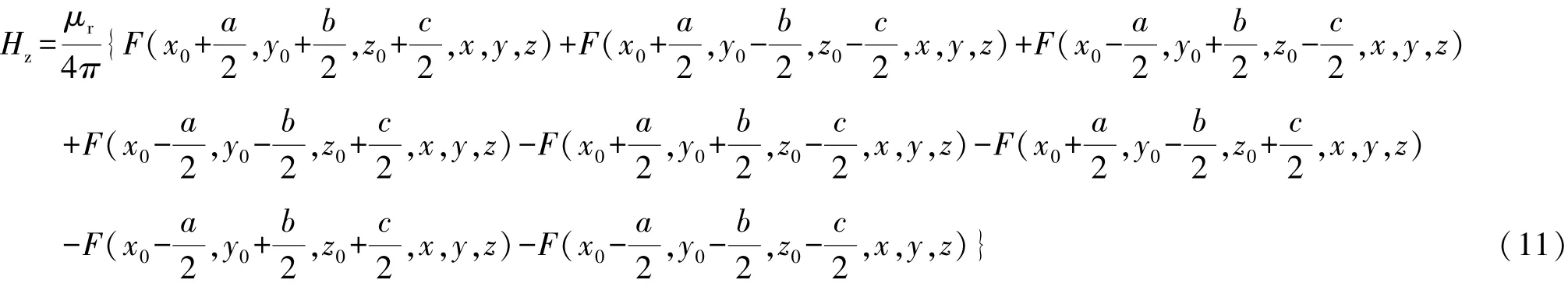
这里:μr为长方体的磁导率，Mx，My，Mz为长方体的感应磁场强度，a，b，c为长方体的长宽高，x0，y0，z0为长方体的形体中心坐标，x，y，z为P点坐标。

3 钢板模型的磁场强度分布

为了验证上述理论的可发现性和正确性，我们选择了一块同时含有两种几何形状的钢板模型材料进行实验。图3为预制钢板模型的正视图和俯视图，钢板材料为20＃无缝碳钢，长宽厚尺寸分别为390 mm、150 mm、18 mm。在钢板中线上预制5个不同大小与孔深的直立圆柱体孔洞，孔洞直径为2 mm～4 mm，孔深为5 mm～15 mm，详细尺寸如图3中标注所示。

图3 预制含直立圆柱体的钢板模型(390 mm∗150 mm∗18 mm)

3.1 钢板模型磁场强度分布理论计算

钢板模型以形体中心作为坐标原点，长度方向为X轴，宽度方向为Y轴，高度方向为Z轴。根据1的理论公式，作者应用VC＋＋编制计算软件[15]，对钢板模型的磁场强度进行理论计算，并绘制强度等值线图，其理论等值线分布如图4所示。钢板模型的X剖面磁场强度曲线如图5所示。

观察图4、图5，我们可以明显地发现缺陷引起的磁场异常与钢板模型的几何量有着非常明显的对应关系，对图3、图4与图5进行比较，说明异常体的位置更可以通过磁场异常曲线位置得到准确的判断。

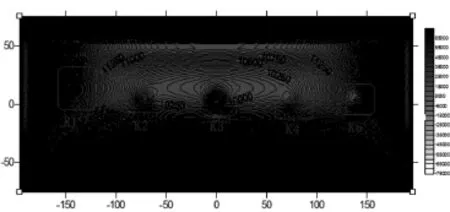
图4 磁法探测理论下钢板模型的磁场强度分布图

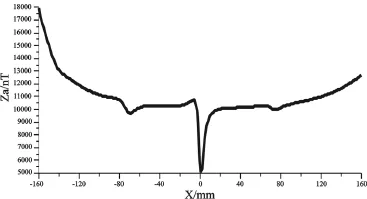
图5 磁法探测理论下钢板模型的X剖面磁场强度曲线

3.2 钢板模型磁场强度分布实测

为了进一步验证理论公式的正确性，实测实验采用俄罗斯“动力诊断”公司利用金属磁记忆方法开发出了独特的仪器——应力集中磁检测仪(TSC－1M－4)。此仪器利用了工件在工作中形成的残余应力在物体应力集中区产生磁场。通过磁场Hp分布同残余应力之间的关系，来测定设备应力集中区，进而找出结构的薄弱部位。该仪器有3个通道，每个探头之间的距离为5 mm。

实测实验以步长1 mm对钢板模型进行九次检测，覆盖整个模型板面。应用该仪器测量钢板模型所得磁场分布图如图6所示。

图6 TSC－1M－4探测所得磁场分布图

比较图4、图6，可以清楚看到TSC－1M－4探测所得磁场分布图(未进行滤波除噪)与理论磁场分布图中，K1～K5，5个磁场异常区一一对应，证明了理论与实践具有良好的符合性，为磁法探测能否应用于钢结构进行了定性分析。

4 钢结构体变形体磁场正演实验

4.1 正演方案

公式(2)、(3)、(4)为我们提供了计算长方体的磁场的方法。但是图7中斜线阴影线的变形钢结构体不再是规则的，我们已知的理论公式不再适用。

积分理论告诉我们:在一个有界区域内应用剖分形体是可以求一个不规则体的近似物理量。观察公式(2)，其所需参数分别为钢结构体中心点坐标，探测点坐标和磁场参数。而后二者为已知条件，故解决钢结构体中心点坐标为问题的所在。

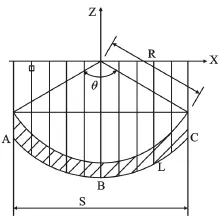
图7 中间承压变形后的长方体二维示意图

图7 中的竖线阴影线为弯曲长方体剖分示意图，A，B，C为带探测的3个试验点，S为弯曲长方体的弦长，L为弧长，R为长方体中线圆弧的半径，θ为圆弧对应的圆心角。由图7可知，在剖分数目足够大的情况下，每个剖分部分近似为一段长方体，而这些长方体的中心刚好是在一段圆弧上。以这段圆弧的圆心为坐标原点建立一直角坐标系，假设钢板承压变形一般表现为图中的向下关系，即Y为零，故我们只需建立X－Z二维坐标系。

在已知弧长L，圆弧中点偏移中心线位移H下，我们可以容易的求出弦长S，半径R，圆弧对应角θ。

记公式(2)为f(x，y，z，a，b，c，X，Y，Z)，其中x，y，z为长方体的形体中心坐标，a，b，c为长方体的长宽高，X，Y，Z为待探测点的坐标。

式中a＝｜(xi＋xi＋1)/2｜

剖分次数n的大小决定了剖分计算的精度，由于应力集中磁检测仪(TSC－1M－4)的最大探测精度为0.25%，故为了满足以后实验验证精度要求以及顾及解算速度，这里选取千分之一为最大精度，实际操作中以保证Hzi＜0.01为准。最后作者在应用C＋＋语言编制了解算程序。

4.2 不同变形程度实体模型的正演实验

图8中6个模型都由一个0.3 m×0.03 m× 0.008 m的20＃钢板弯曲得到，以圆弧对应圆心为坐标原点，其弧长都为0.3 m，而偏移量H和半径R都如图中所示。由式(12)中的方法计算得到的A、B、C三点的磁场强度如表1所示。值得注意的是，为了清楚看出B点与A，C两点的关系，该正演中地磁场参数只取Z方向，即Mx＝0 nT，My＝0 nT，Mz＝31 520 nT。

图8 6个弧长都为0.3 m的承压弯曲板体模型的二维示意图

6个模型的主要参数及其A，B，C三点的磁场强度 表1

图9 B点偏移量

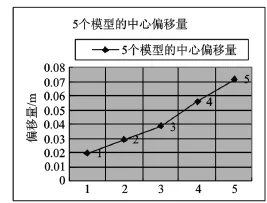
图10 B点磁场强度图

为了更好地观察表中磁场强度数据与变形偏移量的对应关系，对表1中的偏移量与B点的磁场强度关系作折线展示，如图9、图10所示。通过观察可以看出，模型中心偏移量的变化与模型中心磁场强度的变化具有良好的相关性。

由前4组数据，利用Matlab中的cftool工具箱得到B点的磁场强度关于偏移量的曲线方程为:

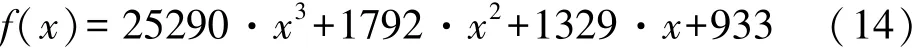
其中SSE为0.00043，R－square为0.999 999 911 862 153 8。利用第5组数据对拟合来的曲线方程进行检验，得f(0.0716)－1046.62＝0.02，这检验了拟合方程的准确性。

5 结论与展望

5.1 结论

本文根据钢结构易被磁化的特点和具有材质和变形控制的多重检测需求，对磁法探测在钢结构检测领域的应用做了必要的基础性研究，通过对磁法探测基本原理的研究，探讨了磁场强度与几何解析量的必然关系，并对其可行性和准确性进行了必要的计算与实验，得出了一些有益的结论:

(1)本文以磁场强度与几何量的原理模型为基础的优化模型，可以适用于钢结构变形监测中的几何量解析，其正确性得到实测实验数据证实；

(2)以剖分方法建立的非规则体的磁场强度与几何挠度的整体关系具有必要的精度保证，同时通过曲线拟合可以解决偏移量与磁场强度的相关性问题。

5.2 展望

本文对于磁场的处理进行的研究还仅仅完成了基础模型建立，以及必要的计算与实验对比，而钢结构等检测的实际中磁场要复杂得多，故解决实际磁场下的变形监测还需在以下方面加以深入研究:

(1)变形量检测值的获得和精度评价，还需要大量实际磁场强度探测值为基础的反演模型和反演计算，从而进一步验证该理论与方法实用性；

(2)通过本文的二维变形检测方法为基础，向三维检测方向进一步发展与完善，最终建立钢结构磁法探测变形的系统理论与方法。

[1] 黄向阳，刘占林，马建明等.大跨度空间钢结构精密工程测量技术方案研究[J].测绘通报，2009(08):39～43

[2] 崔旭升，李法理，周少平等.基于全站仪交会的变形监测方法的应用研究[J].测绘工程，2007(05):20～22

[3] 于承新，李妍.基于数字摄影的钢结构变形监测系统研究[J].测绘信息与工程，2002(02):14～15

[4] 于承新，张超，李宪立等.数字摄影技术测量结构变形的应用探索[J].勘察科学技术，2001(06):49～53

[5] 胡友健，梁新美，许成功.论GPS变形监测技术的现状与发展趋势[J].测绘科学，2006(05):155～157

[6] 赵群，刘键，陈金科.应用激光扫描法对国家体育馆大跨度钢屋架滑移过程变形监测与分析[J].测绘科学，2007 (03):110～111

[7] 刁建鹏，黄声享.CCTV新台址主楼变形监测分析[J].测绘工程，2009(05):63～65

[8] 莫南明，过静珺，张胜良等.CCTV主楼施工变形监测技术应用研究[J].测绘工程，2007(05):48～52

[9] 管志宁.我国磁法勘探的研究与进展[J].地球物理学报. 1997(S1):299～307

[10] 管志宁，郝天珧，姚长利.21世纪重力与磁法勘探的展望[J].地球物理学进展，2002(02):237～244

[11] 祁光，吴燕冈，严加永.磁法勘探在寻找金属非爆炸物中的应用[J].吉林大学学报(地球科学版)，2008(S1):30～32

[12] 管志宁.地磁场与磁力勘探[M].北京:地质出版社，2005

[13] 莫撼，邓居智.场论[M].北京:原子能出版社，2006

[14] 邓居智，莫撼.场论习题解题指南[M].北京:原子能出版社，2007

[15] 钱能.C＋＋程序设计教程[M].清华大学出版社，2005

Deformation Monitoring of Steel Structure Based on Magnetic Method Probing Theory

Qiu ZiHan，Xiong ZhuGuo，Liu XiangTong，Shen BaoLong，Hu Xin
(East China Institute of Technology，Fuzhou 344000，China)

The objective condition of Magnetic Method Probing Theory can be used in deformation monitoring of steel structure are the magnetizability of steel structure and the stability of earth magnetic field.With the application of high precision magnetic field strength measuring instrument and the computer technology，Magnetci Method Probing Theory comes into a period of high－accuracy survery and automatic calculating.In this paper，authors use the relation principle between magnetic field strength and spatial location to establish the optimized mathematical model of Magnetci Method Probing Theory in deformation monitoring of steel structure，use subdivision method of integral theory to resolve the calculating problem of magnetic field strength of anomalistic steel structures，through the forward experiment of examination data of steel structure who has been anamorphic under the pressure，obtain the dependent equation between deflection and magnetic field strength，discover that the split times determine the precision of subdivision calculations，all of these is a brand－new searching for deformation monitoring of steel structures.

magnetic field strength；deflection；anomalistic steel structures；forward；subdivision

1672－8262(2011)01－150－06

P631.2

A

2010—11—22

邱子汉(1986—)，男，在读硕士研究生，主要从事变形监测方法与数据处理方面研究。

核资源与环境教育部重点实验室基金项目(081211)