基于ArcGIS的SRTM缺失数据修复处理方法

徐良，彭光雄，沈蔚

(1.常州市测绘院，江苏常州 213000； 2.中南大学地学与环境工程学院，湖南长沙 410083；3.大洋生物资源开发与利用上海市高校重点实验室，上海海洋大学，上海 21306；4.有色金属成矿预测教育部重点实验室，湖南长沙 410083)

企业风采

基于ArcGIS的SRTM缺失数据修复处理方法

徐良1∗，彭光雄2，4，沈蔚3

(1.常州市测绘院，江苏常州 213000； 2.中南大学地学与环境工程学院，湖南长沙 410083；3.大洋生物资源开发与利用上海市高校重点实验室，上海海洋大学，上海 21306；4.有色金属成矿预测教育部重点实验室，湖南长沙 410083)

利用栅矢转换和掩膜技术及ArcGIS的空间插值模块，构建了一种SRTM缺失数据的修复处理方法。通过不同条件下的多种样本试验，探讨了外界因素对插值精度和运算效率的影响。结果表明样条函数法是适宜于SRTM缺失数据修复的最佳插值方法。当人工模拟的空洞窗口大小为4×4像元时，其插值的误差平均值和标准差分别为0.90%和0.75%。随着地形起伏程度的增加，插值误差的平均值和标准差也随之加大。同时插值的精度会随着空洞窗口的增大而降低，窗口大小从4×4像元增大至12×12像元时，误差平均值从0.92%增加至3.84%，标准差则从0.75%增加至3.26%。试验表明6×6像元的窗口大小是保障插值误差在SRTM数据精度范围内的最大窗口。

SRTM；数据修复；空间插值；ArcGIS

1 引 言

美国等航天飞机雷达地形测量(Shuttle Radar Topography Mission，SRTM)的数字高程数据是地理空间建模的重要基础数据，在地学研究中得到广泛的应用[1～5]。然而由于雷达信号受到干扰、或者发生镜面反射、雷达阴影或回波滞后等情况导致SRTM高程数据在水域、高山区和峡谷地区存在有小块的数据空缺点、空白区。国内外对SRTM数据空洞的填补方法展开了广泛的研究[6～10]。主要的方法有以下3种类型:一是利用相应的其他高分辨率数字高程数据直接填充；二是利用空间插值方法进行填充[6，7]；三是利用其他辅助数据源进行数据融合后填充[8～10]。其中空间插值方法仍是当前研究的主流，主要包括几何法、统计法、空间统计法、函数法、随机模拟法、物理模型模拟法和综合法等[11]。还有的学者将分形和形态学滤波等方法应用到地形数据内插中来[12～15]。修复SRTM缺失数据的内插方法多种多样，研究者针对某一种特定的修复方法，往往只能自行编写程序，方能实现SRTM缺失数据的修复。即使这种修复方法本身是优秀的，却需要广大的应用人员去编写繁杂的软件程序来实现其功能，则其实际应用的可操作性将大大降低。因此如果能基于一种主流或通用的软件工具，通过某种有效的流程计算即可实现上述目的，则对于地学研究人员更加广泛高效地利用SRTM数据具有重要的意义。

本文以主流的GIS平台ArcGIS 9.3为工具软件，通过构建合理有效的SRTM缺失数据修复处理流程，基于其自身的插值工具，在比较多种插值方法计算性能的基础上，优选出了相对最为优良的插值方法，为SRTM数据的广大用户填充修复缺失数据提供了一种方便实用而有效的解决方案。

2 SRTM缺失数据的处理方法

2.1 数据来源

SRTM项目于2000年由美国、意大利和德国等多家国际机构共同发起承担，其任务是用于获取全球范围高精度的数字地形。SRTM产品包括3种不同分辨率的数字高程模型(Digital Elevation Model，DEM)数据:SRTM1数据覆盖范围仅仅包括美国大陆，其空间分辨率为1弧秒(30 m)；SRTM3数据覆盖全球，空间分辨率为3弧秒(90 m)；SRTM30数据同样覆盖全球，空间分辨率是30弧秒(1 000 m)[16]。针对数据缺失问题，Filled finished版的SRTM产品虽然已经对少于16个连续数据点的缺失区域进行了填补，但是其余面积较大的数据缺失区域仍没有进行处理。因此SRTM的数据缺失现象依然存在(如图1a)，必须进行修复处理才能进行实际应用。本文从GLCF网站下载了中国境内的一幅SRTM3数据作为试验数据，产品编号为SRTM_ffB03_p124r039[17]，空间分辨率为90m，标称绝对高程精度±16 m，绝对平面精度±20 m[16]。

2.2 基于ArcGIS的空间内插算法比较

ArcGIS是当前主流的GIS软件平台，在地学分析中得到广泛的应用。反距离加权方法(Inverse Distanceto a Power，IDW)、克里金法(Kriging)、最近距离法(Nearest Neighbor，NN)、样条函数法(Spline)等是ArcGIS软件中几种较为经典的空间插值方法。对于不同的空间插值方法而言，没有绝对最优的空间内插方法，只有特定条件下的最优方法[11]。根据ArcGIS空间插值模块的自身特点和SRTM数据的内在特征，通过比较分析和检验多种不同条件下的插值试验结果，最后选择出适宜于SRTM缺失数据修复的最优空间内插方法。

选择SRTM数据中地貌类型丰富且没有数据空洞的区域切割后作为测试数据。在测试数据中选择不同地貌类型所在位置区域设置16个4×4像元窗口大小的检测样本(如图1b)；在同一地貌区域设置1×1像元至12×12像元共12个不同窗口大小的检测样本(如图1c)。

图1 SRTM数据空洞及测试样本分布示意图

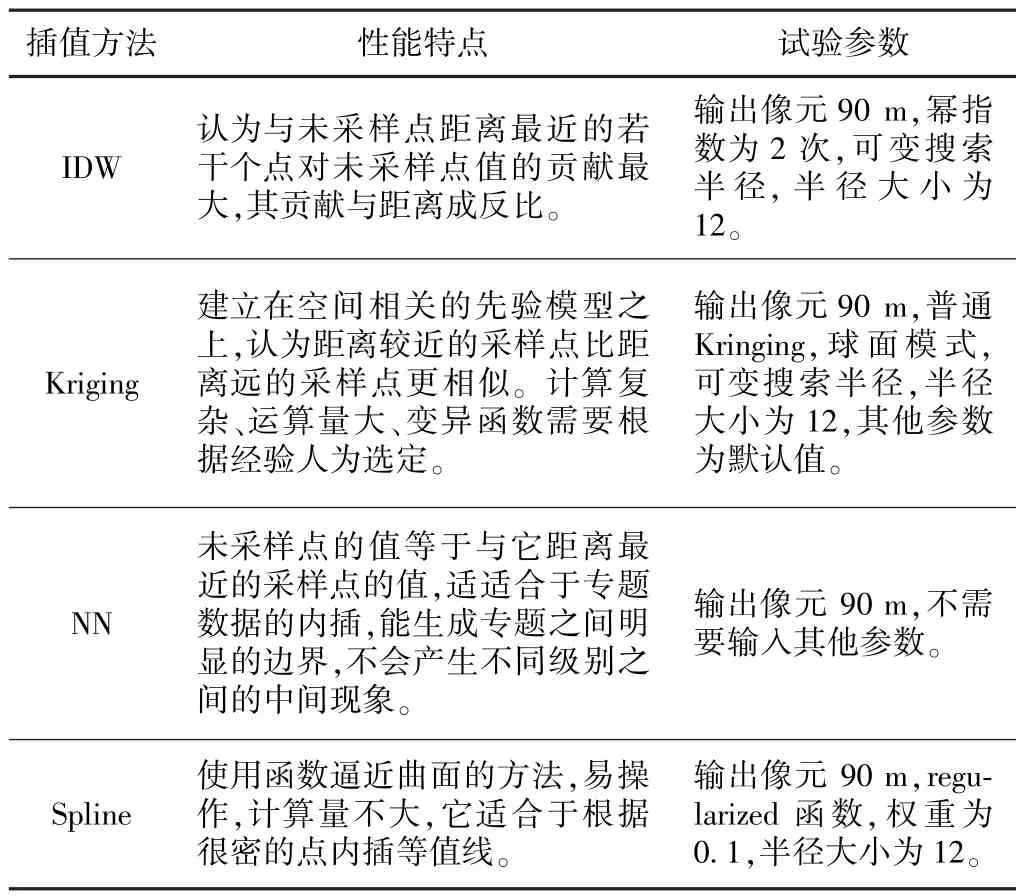
插值方法的性能特点和试验参数 表1

以ArcGIS 9.3为插值工具软件，利用IDW、Kriging、NN和Spline等4种插值方法对4×4像元窗口大小的16个样本和不同窗口大小的12个样本进行插值比较分析。插值方法的性能特点[11]和所采用的插值试验参数见表1所示。通过这组插值试验，比较分析了相同条件下不同插值方法对插值结果的影响、地形起伏大小对插值结果的影响、缺失数据的面积大小对插值结果的影响以及不同插值方法的计算效率等4种

2.3 SRTM缺失数据修复流程与处理

很多文献中提到的基于栅格数据的空间插值一般只描述了插值方法的工作原理，对于具体的插值过程往往很少进行说明[10，18]。而实际情况中插值过程的不同，会导致插值结果的显著差异，特别是利用现有的插值工具软件进行栅格数据的空间插值处理。以基于ArcGIS 9.3的SRTM空洞数据插值为例说明如下。ArcGIS 9.3的Geostatistical Analyst模块既可以对栅格数据也可以对矢量点数据进行空间插值，而Interploation模块则仅能对矢量点数据进行空间插值。用Geostatistical Analyst模块对带有人工空洞的SRTM栅格数据直接进行插值，所得的结果如图2a所示，可见空洞区域并没有得到合理的填充。由于空洞区域的像评价指标，探讨了外界因素对插值的影响，从而优选出适宜于SRTM缺失数据修复的最佳插值方法。试验选取完好的SRTM数据在各个样本区域通过人工填充负值(－32 768，跟真实的缺失数据值一致)的方式模拟SRTM缺失数据的空洞，并由此获得用于计算插值精度的真实值。插值结果的精度用误差百分比来衡量，其计算方法如公式1所示。元本身是有值的(－32 768)，只不过是缺失的无效值而已，ArcGIS的插值模块对此无法进行判别而仍当作正常值进行处理，从而导致空洞区域的像元仍然保留插值前的值。因此利用ArcGIS软件进行SRTM栅格数据直接插值来填充空洞区域的方法是行不通的。

解决上述问题的思路是对SRTM空洞区的缺失数据先进行一个预处理，使得ArcGIS仅对有效数据进行插值而对缺失数据不插值。首先，利用Conversion Tools模块的Raster to Point工具将SRTM栅格数据转为Shape格式的点矢量文件；其次，通过Shape点矢量文件的属性表对所有值为－32 768(缺失值)的点进行选取并删除；最后，对不包含缺失值的Shape点矢量文件进行插值。

图2b是没有去除空值点的矢量点插值的结果，其实质是跟栅格数据直接插值是相同的，从而所得到结果也是不合理的。这是由于每个点位上该点自身的权重是最大的，两点之间的距离为90 m(由SRTM数据的空间分辨率决定)，当插值输出像元大小为90 m时，则插值的结果其实就是将每个点自身的值(－32 768)赋给该点，从而在图2b中形成一条值为－32 768的封闭等值线。图2c是去除空值点后的矢量点插值的结果，由于消除了缺失值点的影响，则在图2c中形成多条相互连通的等值线。

基于ArcGIS的SRTM缺失数据修复方法的总体流程如图3所示。利用Conversion Tools模块的Raster to Point工具实现栅矢转换；利用Attributes属性表剔除缺失点数据；利用Interploation模块将矢量点数据插值生产栅格数据；利用Reclass模块的Reclassify工具以－32 768为阈值提取空洞掩膜Mask(0，1)和Mask(1，0)，如图4b所示；利用Math模块的Times(乘)和Plus (加)运算进行掩膜处理，如式(2)所示；最终得到SRTM的缺失数据的修复结果，如图4c所示。

图2 栅格数据和Shape点矢量数据插值结果比较

图3 基于ArcGIS的SRTM缺失数据修复流程

图4 SRTM缺失数据修复前后比较

式中，SRTM是修复后的数据，SRTM1是带有空洞的数据，SRTM2是插值后的数据，Mask(0，1)是空洞赋值为0的掩膜，Mask(0，1)是空洞赋值为1的掩膜。

3 修复处理结果分析与方法评价

3.1 修复处理结果分析

对不同地形条件下的16个4×4像元窗口大小的人工模拟空洞经IDW、Kriging、NN和Spline等4种方法的插试验值进行了统计，结果如表2和图5所示。图5a显示的是16个样本四种不同方法插值精度的比较曲线，误差百分比的平均值由高到低依次为IDW、 NN、Krging和Spline，分别为1.32%、1.13%、1.07%和0.90%，各自的标准差则分别为0.90%、0.81%、0.62%和0.75%。误差的平均值反映出各种插值方法所得结果与真实值的接近程度，标准差则体现了各种方法的稳定性。综合比较分析误差的平均值和标准差的情况，可以看出Spline是这4种插值方法中最佳的一种。图5b显示的是插值精度随地形起伏变化的情况，Spline法插值的结果表明随着地形起伏程度的增加，其误差平均值和标准差也随之加大。误差平均值由0.56%增加至1.21%，标准差则由0.41%增加至1.08%，说明地形起伏越小插值的精度越高，稳定性也越好。

空值区域为4×4窗口的插值统计结果 表2

图5 4×4窗口时的插值统计曲线

图6 不同方法插值运算效率曲线

图7 插值精度随窗口大小的变化曲线

插值精度是反映插值方法性能的重要指标之一，而另一重要指标则是运算效率，特别是对于大规模的插值计算尤其重要。通过截取不同像元总量的SRTM数据，基于同台电脑，利用上述4种方法进行插值试验，得到如图6所示的统计结果。可见相同情况下插值的运算效率由低至高依次为Krging、Spline、IDW、和NN。其中Krging的运算量相对而言非常大、效率十分低下，而Spline和IDW相差不大。结合插值的精度和运算效率，则可进一步判断出Spline是最适宜于STRM数据的插值方法。

在相同地形条件下，人工模拟出1×1像元至12× 12像元共12个不同窗口SRTM数据空洞(如图1c)，并以Spline方法为例测试空洞面积大小对插值精度的影响，统计结果如表3和图7所示。可见，插值的误差百分比随着窗口的增大而逐渐增加，且以误差百分比的最大值增加趋势尤其显著。误差百分比的平均值和标准差的增加趋势基本一致，随着窗口增大在插值精度降低的同时稳定性也随之变小。例如当窗口大小从4×4增大至12×12时，误差百分比的平均值从0.92%增加至3.84%，标准差则从0.75%增加至3.26%。测试窗口所在区域的平均海拔为1 102 m，则该地区4×4窗口插值的平均精度约为±10.2 m，12×12窗口插值的平均精度约为±42.3 m。按SRTM3数据的标称绝对高程精度±16 m来计算，则该地区相应的误差百分比约为1.6%，对应的窗口大小在6×6左右。超出6×6窗口大小插值得到的结果将会引起较大的失真。当然，这种用海拔和数据的标称绝对高程精度所衡量的适宜窗口大小，只是相对意义上的衡量方法，它会随着海拔高度、地形起伏程度以及空洞区域的形状和位置等因素的变化而会有所差异。

不同窗口大小的Spline插值统计结果 表3

3.2 基于ArcGIS的修复方法评价

基于ArcGIS的修复方法，仅仅利用ArcGIS软件本身而不需要编写内插程序就能对SRTM的缺失数据进行修复处理，且操作简单快捷，修复精度高，具有良好的实用效果和广阔的应用前景。通过上述插值精度和运算效率的比较，表明Spline法是基于ArcGIS修复SRTM缺失数据的最佳空间内插算法。该方法可修复缺失数据窗口为任意大小的SRTM数据，当且仅当SRTM的缺失数据的窗口小于或等于6×6像元时，其误差百分比可达1.4%左右，基本可达到SRTM数据±16 m的标称绝对高程精度。

4 结论与讨论

利用ArcGIS软件平台，通过构建合理的处理流程，探讨了一种SRTM缺失数据的修复方法。主要得到以下结论:

(1)利用ArcGIS软件进行SRTM缺失数据的空间插值时，必须先要进行栅矢转换和空值点的剔除处理，才能保证插值结果的有效性；

(2)通过对ArcGIS软件现有的几种插值方法的测试比较，发现样条函数法的插值结果最好，运算效率也较为理想，是最适宜于SRTM缺失数据修复的插值方法；

(3)地形起伏对插值的精度影响较大，随着地形起伏程度的增加，插值误差的平均值和标准差也随之加大；

(4)SRTM缺失数据区域的面积大小和形状也对插值的精度也存在很大的影响，插值的精度会随着空洞窗口的增大而降低。初步的测试结果表明空洞窗口大小在6×6像元以下时基本能保障插值填补数据的精度，而超过此窗口大小时将会产生较大的失真；

(5)测试样本的数量和分布区域有待更进一步的提高和完善，6×6像元的精度保障窗口大小只是一个初步的判断，实际结果会因为地形起伏程度以及空洞区域的形状和位置等因素的变化而会有所差异。

[1] 游松财，孙朝阳.中国流域的SRTM30数据提取与计算[J].地球信息科学学报，2009，11(02):189～194

[2] 龙恩，程维明，周成虎等.基于Srtm－DEM与遥感的长白山基本地貌类型提取方法[J].山地学报，2009，25(5): 557～565

[3] 彭光雄，宫阿都，崔伟宏等.多时相影像的典型区农作物识别分类方法对比研究.地球信息科学学报，2009，11 (02):225～230

[4] 赵尚民，程维明，柴慧霞等.基于遥感与SRTM的青藏高原冰缘地貌信息提取方法—以1∶100万标准分幅拉萨幅(H46)为例[J].地理研究，2007，26(6):1175～1187

[5] Oky D A P，Ayako E，Ryuzo Yo，et al.Supervised landform classification of North－east Honshu from DEM－derived thematic maps[J].Geomorphology，2006，78:373～386

[6] 游松财，孙朝阳.中国区域SRTM90m数字高程数据空值区域的填补方法比较[J].地理科学进展，2005，24(6): 88 92

[7] 王涛，毋河海.SRTM高程数据中空缺单元的内插填补[J].测绘科学，2006，31(3):76 77

[8] Kaab A.Combination of SRTM3 and Repeat ASTER Data for Deriving Alpine Glacier Flow velocities in the Bhutan Himalaya [J].Remote Sensing of Environment，2005(94):463～671

[9] 凌峰，王乘，张秋文.基于ASTER数据和空间误差分析的SRTM无效区域填充[J].华中科技大学学报(自然科学版)，2006，34(12)，108～111

[10] 阚瑷珂，朱利东，张瑞军等.基于数据融合的SRTM数据空洞填补方法[J].地理空间信息，2007，5(3):62～64

[11] 李新，程国栋，卢玲.空间内插方法比较[J].地球科学进展，2000，15(3):260～265

[12] 张山山.分形方法在地形数据内插中的应用.西南交通大学学报，2000，35(2):141～14

[13] Weidner U.，Forstner W.Towards Automatic Building Extraction from High Resolution Digital Elevation Models[J]. ISPRS Journal of Photogrammetry and Remote Sensing， 1995，50，38～49

[14] Kilian J.，Haala N.，Englich M.Capturing and evaluation of airborne laser scanner data[J].International Archives of Photogrammetry and Remote Sensing，Vienna，1996，32，(B3):383～388

[15] Hug C.，Wehr A.Detecting and Identifying Topographic Objects in Imaging Laser Altimeter Data[J].International Archives of Photogrammetry and Remote Sensing，1997，32:19～26

[16] USGS(2004)，Shuttle Radar Topography Mission，1 Arc Second scene SRTM_u03_n008e004，Unfilled Unfinished 2. 0，Global Land Cover Facility，University of Maryland，College Park，Maryland，February 2000

[17] http://glcf.umiacs.umd.edu/data/srtm/index.shtml.

[18] 黄文捷.利用插值算法填补SRTM3 DEM数据空洞的比较分析.江西测绘.2007，69(3):25～28

Method Study on SRTM Void Data Recovery Based on ArcGIS

Xu Liang1，Peng GuangXiong2，4，Shen Wei3
(1.School of Geoscience and Environmental Engineering，Central South University，Changsha 410083，China； 2.The Key Laboratory of Shanghai Education Commission for Oceanic Fisheries Resources Exploitation，Shanghai Ocean University，Shanghai 201306，China； 3.Key Laboratory of Metallogenic Prediction of Nonferrous Metals，Ministry of Education，Changsha 410083，China)

The digital elevation data of Shuttle Radar Topography Mission(SRTM)is an important foundation data for geospatial modeling.However the void data of SRTM caused by the deficiencies of radar produce great inconvenience for its application.An approach and process flow of SRTM void data recovery is constructed using raster to vector conversion and mask processing technology based on spatial interpolation in ArcGIS software.To ensure the validity of interpolation results，the most important step of this process flow is deleting points of void data.The interpolation accuracy and operations efficiency of Inverse Distance to a Power(IDW)，Kriging，Nearest Neighbor(NN)and Spline are compared and analyzed based on a variety of test samples under different conditions.16 test samples of 4×4 pixel window size distribute on different landforms regions，while12 test samples of different pixel window size from 1×1 to12×12 locate on the same landforms region.The hollows of SRTM void data are simulated artificially through fill some negative value to the SRTM data in the areas of test samples.With this way to obtain the true value used to estimate interpolation accuracy.The mean of interpolation error is in decreasing order is IDW，NN，Krging and Spline，whose value is 1.32%，1.13%，1.07%and 0. 90%respectively.Their standard deviation value are 0.90%、0.81%、0.62%and 75%respectively.Results show that Spline interpolation method is the optimal one applicable to recover void data of SRTM.When the artificial simulation window size of empty area is 4×4 pixels，the mean and standard deviation of interpolation error is 0.90%and 0.75%respectively.With the levels of undulating topography increase，the mean and standard deviation of interpolation error will increase accordingly.On the other hand，interpolation accuracy will descend with the accretion of window size.When the window size of empty area increase form 4×4 pixels to12×12 pixels，the mean of interpolation error increased from 0.92% to 3.84%，standard deviation increased from 0.75%to 3.26%.6×6 pixels is the largest window size of empty area which can restrict the interpolation error within the data precision of SRTM.Experimental results show that the approach proposed in this paper is a good way to recover SRTM void data only using ArcGIS software.

SRTM；data recovery；spatial interpolation；ArcGIS

1672－8262(2011)01－5－06

N945.1

A

2010—12—21

徐良(1977—)，男，工程师，主要从事城市测绘与GIS、城市三维等方面的工作。

中国博士后科学基金(20080430586)；大洋生物资源开发与利用重点实验室开放基金(B－8208－07－0001－1)。