Excel在GM(1，1)沉降预测数据处理中的应用

黄维腾

(茂名市粤能电力股份有限公司设计院，广东茂名 525000)

Excel在GM(1，1)沉降预测数据处理中的应用

黄维腾∗

(茂名市粤能电力股份有限公司设计院，广东茂名 525000)

GM(1，1)模型在沉降预测中已经广泛应用，然而其计算过程复杂，在数据量较多的情况下计算量很大。本文以某沉降监测数据为例，提出利用Excel进行数据处理的方法，过程简单，结果准确，极大方便了计算工作。

Excel；GM(1，1)；沉降预测；数据处理

1 前 言

随着现代化进程的不断加快，城市各类高层建筑日益增多。由于建筑物的增高，荷载的增加，在地基基础和上部结构的共同作用下，建筑物可能发生不均匀沉降，轻者将使建筑物产生倾斜或裂缝，影响正常使用，重者将危及建筑物的安全，因此，必须对其进行沉降观测。

高层建筑沉降监测的目的不仅仅是观测其沉降值，更为重要的是根据已观测的量值，通过建立一定的模型来预测其在未来某一时刻的可能沉降值，进而分析其安全性，将可能的损失消除在萌芽状态或最大限度地减轻损失。沉降预测有回归分析法、确定函数法、时序分析法等，但这些方法通常要求有大量样本，而且要求具有典型的概率分布，这在实际工作中往往难以满足。沉降预测中既包含已知信息，又有未知信息而且处于变化之中，这样预测沉降量未来变化的问题，实质上可以看作一个灰色问题[1，2]。

2 GM(1，1)预测模型简介

GM(1，1)模型是灰色理论中最常用的模型之一。它的建模是对生成数列的建模，它对原始数据没有大样本的要求，只要原始数列有4个以上的数据就可以通过变换来建立模型。目前GM(1，1)模型在建筑物沉降预测中有着广泛的应用，并取得了良好的效果[3，4]。

GM(1，1)计算过程如下:

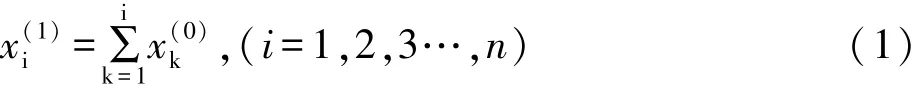
(2)利用此序列生成紧邻均值序列z(1)(k)为

(3)建立灰色GM(1，1)模型的一级白化微分方程

(4)灰色GM(1，1)模型参数列A＝[a，b]T的最小二乘估计为

将计算求得的参数a，b带入式(1)中求微分方程，取x(1)(0)＝x(0)(0)，可得到灰色GM(1，1)预测模型为:

(5)对此式再做一阶累减还原计算得到原始序列x(0)的灰色GM(1，1)预测模型为:

3 基于Excel的GM(1，1)数据处理[5]

3.1 数据准备

某高层建筑沉降观测要求每月监测一次，共计观测16次，取得了丰富的数据。为了便于计算，选择一个有代表性的沉降观测点说明，数据如图1所示。

在数据录入后，在C2单元格中输入公式“＝B2”；在C3单元格中输入公式“＝B3＋C2”，回车。将光标指向C3单元格的右下角，待其变成细小的黑十字后双击或下拉至C17，即可得到全部累加生成结果，如图1所示。

在D3单元格中输入计算公式“＝－AVERAGE (C2:C3)”，回车，将光标指向D3单元格的右下角，待其变成细黑十字后双击或者下拉至D17，即可得到全部移动平均的负值，如图1所示。

在E3－E17添加一列数字1，这些1与移动平均的负值并排，构成用于估计参数的矩阵B。然后将原始数据从B3－B17复制并粘贴到B矩阵的右侧，如图1所示，这样就完成了数据预备工作。

图1 数据预备图

3.2 最小二乘运算

(1)计算矩阵BTB及其逆矩阵(BTB)－1。选定一个2∗2的单元格区域，如G3:H4，然后借助Excel的矩阵乘法函数mmult和矩阵转置函数transpose，输入计算公式

同时按住Ctrl＋Shift键，回车，即可得到BTB的计算结果，如图2所示。

选定一个2∗2的单元格区域，如G7:H8，借助Excel的矩阵求逆函数minverse，输入计算公式:

同时按住Ctrl＋Shift键，回车，即可得到(BTB)－1的计算结果，如图2所示。

(2)计算向量BTY。选定一个2∗1单元格区域，如G11:G12，然后输入计算公式:

同时按住Ctrl＋Shift键，回车，即可得到BTY的计算结果，如图2所示。

(3)计算向量(BTB)－1BTY。选定一个2∗1的单元格区域，如G15:G16，然后输入计算公式:

同时按住Ctrl＋Shift键，回车，即可得到(BTB)－1BTY的计算结果，如图2所示。这个向量给出了GM (1，1)模型的参数估计值:

图2 参数计算图

3.3 建设模型

将计算得到的参数估计结果赋予GM(1，1)模型即可。

3.4 预测与检验

(1)重新整理数据，将观测时间变为从零开始的时序，并输入表格中，同时将参数复制到数据附近，如图3所示。

(2)计算累计数据的预测值。根据GM(1，1)模型及参数，在D2单元格中输入计算公式:

然后将鼠标光标指向单元格D2的右下角，待其变成细黑十字，双击或下拉，即可得到累加数据预测值的计算结果，如图3所示。如果将时序继续延伸，即可继续预测。

图3 预测结果图

(3)累加数据预测值的递减还原。在E2单元格中输入计算公式“＝D2”，回车；在E3单元格中输入“＝D3－D2”，然后将鼠标光标指向单元格E3的右下角，待其变成细黑十字，双击或下拉，即可得到累加数据预测值的递减还原结果，如图3所示。

(4)计算绝对误差与相对误差。

利用Excel计算绝对误差与相对误差过程比较简单，本文不再叙述，计算结果，如图4所示。

图4 绝对误差与相对误差计算图

4 Excel在数据处理中的优势

(1)数据处理方便

利用Excel可以很方便的准备整理原始数据，且整理后的数据能够直接进行计算。

(2)计算快捷

在GM(1，1)模型中参数运算中需要最小二乘运算，计算量很大，利用Excel的矩阵乘法函数、矩阵转置函数、矩阵求逆函数可以快速的得到计算结果，且数据准确，无人为计算误差。

(3)可以方便的检验结果

可以直接利用Excel的计算结果进行检验，计算出绝对误差与相对误差。

5 结 论

利用GM(1，1)模型进行沉降预测数据量较大，使用传统方法进行计算费时费力且容易出错，利用软件编程计算对普通工作者有一定的难度，利用Excel软件进行计算可以方便地进行数据整理，借助Excel函数计算快捷易用，并可方便地进行误差检核，在实际工作中有一定的应用价值。

[1] 邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社，1987

[2] 李日云，王利，张双成.灰色预测模型在高层建筑物沉降预测中的应用研究[J].地球科学与环境学报，2005，27 (1):84～87

[3] 何涛，刘玉财，羊远新.机场沉降监测数据处理的探讨[J].城市勘测，2009(4):134～137

[4] 冯锦明，李炳芳.灰色预测模型在建筑物沉降监测中的应用[J].地矿测绘，2008，24(2):7～9

[5] 陈彦光.基于Excel的地理数据分析[M].北京:科学出版社，2010

Application of Excel to the Data Processing in the GM(1，1) Settlement Predication

Huang WeiTeng
(Maoming Yueneng Electrlc Power Co.，Ltd.Maoming 525000，China)

GM(1，1)model has widely used in the settlement predication.As its complex calculating process，the amount of calcuation is very great under the condation of a large quantity of data.Taking an settlement monitoring data as an example，this article puts forward the mean of data handling by Excel.The result shows that it has the advantages of simplicity and accuracy and it is a great convenience for calculation.This mean also has a certain application value in the GM(1，1)settlement predication.

Excel；GM(1，1)；Settlement Predication；Data Handling

1672－8262(2011)01－113－03

P209

B

2010—07—12

黄维腾(1979—)，男，工程师，主要从事工程测量、电力测量工作。