数学问题意识的模糊多属性评价研究
2011-04-18束永祥
束永祥,卢 蕊
(1.镇江高等专科学校 基础部,江苏 丹阳 212300;2.镇江高等专科学校 学报编辑部,江苏 镇江 212003)
0 引言
1965年,美国著名控制论专家查德(L.A.Zadeh)教授撰写了一篇用数学方法研究模糊现象的论文“Fuzzy Sets”(《模糊集合》),首次提出了模糊集合的概念,开创了模糊数学研究的新领域[1-4]。
模糊数学作为继经典数学、统计数学之后发展起来的一门新的数学学科,涉及纯粹数学、应用数学、自然科学、社会科学等许多方面,其发展主要在应用方面,已经遍及理、工、农、医及社会科学的各个领域。模糊数学的出现,把数学的应用范围从确定性领域扩大到了模糊领域。采用模糊集合描述具有模糊性的概念,使用模糊数学的方法,如模糊聚类分析、模糊模式识别、模糊综合评价、模糊信息处理、模糊控制、模糊预测与决策等,描述人们的判断、推理、评价、决策和控制过程成为可能[1-7]。
在实际研究中,常常会遇到评价目标与评价指标均带有一定模糊性的情况,此时,运用模糊评价技术进行综合分析,效果会更加理想。对于学生的数学问题意识、问题提出能力的研究,也可以借鉴这些方法,本文主要采用模糊多属性评价方法进行研究。
1 模糊多属性评价方法
1.1 基本原理
模糊评价是在模糊环境下或者模糊系统中,对评价论域中的对象进行排序,或按某些模糊限制条件从评价域中选择出最优对象的数学理论和方法。
1.2 基本步骤
1.2.1 给定模糊集合
给定一个评价对象集A={A1,A2,…,Am}和相应的评价指标集B={B1,B2,…,Bn},并给定每个评价指标相对重要程度的权重集合w={w1,w2,…,wn}。
1.2.2 构造模糊指标值矩阵
把集合B,集合w中的属性指标表示成三角形模糊数,进而得到模糊指标值矩阵[1-4]。
1)将各指标数据和权重向量用三角形模糊数表达。记F(R)为R上的全体模糊集,设G∈F(R),如果G的隶属度函数μG表示为
式(1)中,a≤g≤b,则称G为三角形模糊数,记为G=(a,g,b)。
定性指标可以利用三角形模糊数比例法转化为定量指标,具体的转化形式见表1。精确的定量指标值c可以表示为:c=(c,c,c)。权重向量w=(w1,w2,…,wn)的三角形模糊数表示与之类似。

表1 定性指标向定量指标转化的三角形模糊数比例法
2)构造模糊指标值矩阵。所有的评价属性指标全部化为三角形模糊数后得到的矩阵F=(fij)m×n称为模糊指标值矩阵。
3)模糊指标矩阵F归一化处理。因为不同的评价指标有不同的量纲,为了使数据之间具有可比性,需要对数据进行标准化处理。一般地,针对各个评价指标,m个评价对象在F中都分别有m个模糊指标值,记为xi=(di,ei,fi)(i=1,2,…,m)。根据xi所属指标类型不同,分别使用不同的化归公式进行数据的归一化处理:其中,式(2)为成本型指标的归一化公式,式(3)为收益型指标的归一化公式。
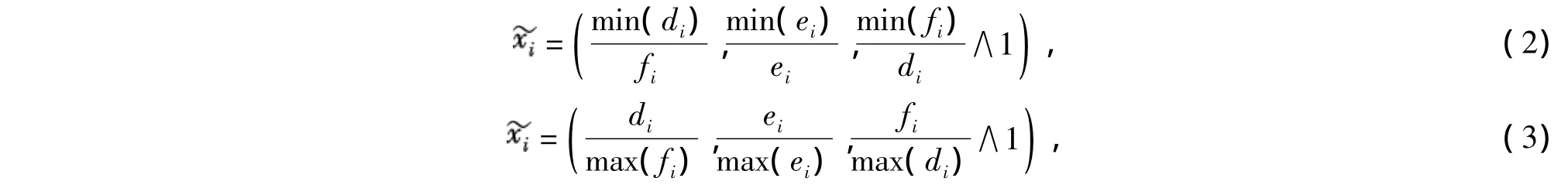
设归一化后的模糊指标值矩阵为C=()m×n[1-4]。
1.2.3 构造模糊评价矩阵
将模糊指标值矩阵F和模糊权重向量w利用广义模糊合成算子实施变换后得到模糊评价矩阵C=(rij)m×n,其中rij=wΘ,i=1,2,…,m,j=1,2,…,n。
1.2.4 模糊选优排序
采用折衷型模糊多属性评价方法,先虚拟模糊正理想和模糊负理想,以加权欧氏距离为测度工具,计算各评价对象与模糊正理想的距离Di+及其与模糊负理想之间Di-,再根据各评价对象从属于模糊正理想的隶属度,比较各评价对象的相对优劣[1-4]。
1)确定模糊正理想M+与模糊负理想M-。模糊评价矩阵C中各列的极大值组成M+,极小值组成M-。
2)确定Di+和Di-。
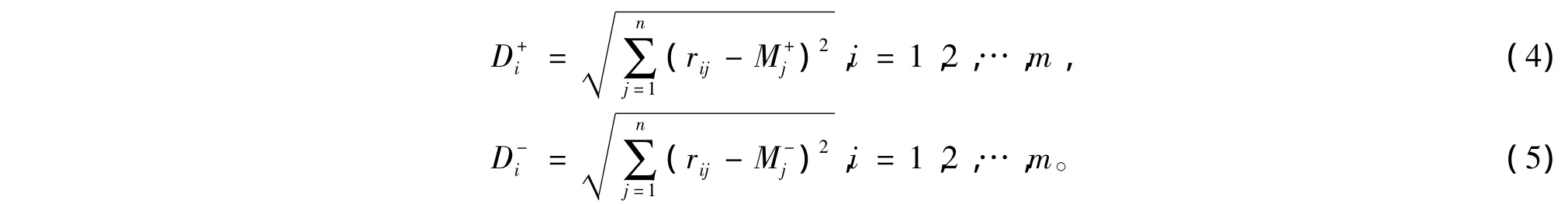
3)确定评价对象属于模糊正理想的隶属度。评价对象i从属于模糊正理想的隶属度为
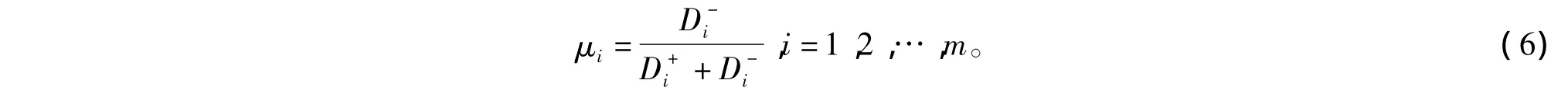
4)选优排序。按隶属度μi从大到小进行排序,根据排序结果可以判断评价对象的相对优劣。
2 数学问题意识模糊评价
数学问题意识是指人们在进行数学的认识活动中,对既有知识经验和一些难以解决的实际或理论问题所产生的怀疑、困惑、焦虑、探究等心理状态,并在其驱动下,不断提出问题、解决问题[8-9]。
2.1 选取研究对象
选取某高校五年一贯制师范专业一年级(A1)、二年级(A2)、三年级(A3)的学生为研究对象,进行研究。
2.2 确定影响因子
主要选取文献[8]提出的影响数学问题意识、问题提出的因素:直觉思维与概括(x1)、合理的数学认知结构或图式(x2)、反省思维(x3)、批判性思维(x4)、数学符号意识(x5)、转化意识(x6)、数学学习中思维结构的简缩(x7)、空间想象力(x8)、一般化与特殊化(x9)、数学信念(x10),共计10个,作为主要影响因子。
2.3 数据统计
三个年级的学生在10个指标上的均分如表2所示。10个指标依专家讨论的重要程度取其权重,权重向量为w=(0.15,0.15,0.10,0.15,0.05,0.10,0.10,0.05,0.10,0.05)。

表2 三个年级的学生10个影响因子分值
2.4 数据的三角形模糊数表示
将上述属性指标以及权重数据统一量化为三角形模糊数后,得到模糊指标矩阵F=(fij)m×n和wT。

2.5 模糊指标矩阵F归一化处理
本研究中3个评价对象的各评价指标量纲一致,归一化后的模糊指标矩阵C=()m×n=F。
2.6 构造模糊决策矩阵
将归一化后的模糊指标矩阵C进行加权处理,得到模糊评价矩阵D=(rij)m×n。

2.7 确定模糊正理想M+与模糊负理想M-
模糊正理想与模糊负理想分别为:
M+=(0.9030,0.8610,0.5660,0.7890,0.3275,0.6060,0.7850,0.2810,0.7320,0.3860),
M-=(0.8205,0.7920,0.5190,0.7230,0.3160,0.5390,0.7560,0.2725,0.7100,0.3840)。
根据公式(4)和公式(5),计算3个评价对象与模糊正理想、模糊负理想之间的距离,结果见表3。
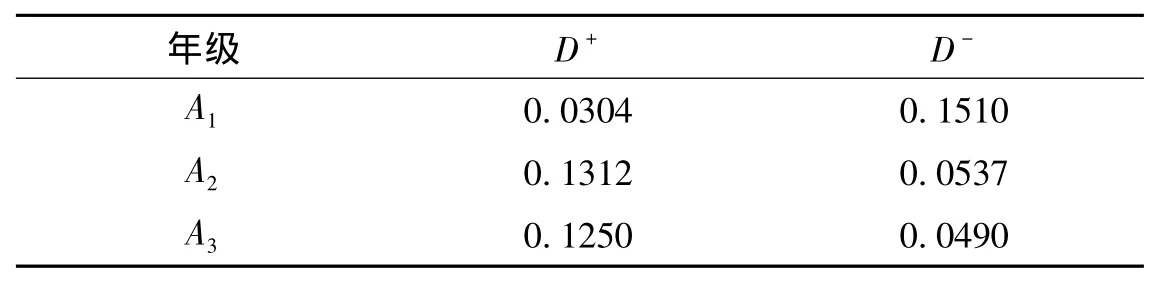
表3 3个评价对象与模糊正理想、模糊负理想之间的距离
2.8 模糊优选决策
设3个评价对象i以隶属度μi从属于模糊正理想,按照公式(6)计算3个评价对象的隶属度,结果分别为:0.8326,0.2902,0.2817。
[1]曹炳元.应用模糊数学与系统[M].北京:科学出版社,2005.
[2]刘林.应用模糊数学[M].西安:陕西科学技术出版社,2008.
[3]王培庄,韩立岩.应用模糊数学[M].北京:首都经济贸易大学出版社,1989.
[4]李柏年.模糊数学及其应用[J].合肥:合肥工业大学出版社,2007.
[5]程乾生.属性集和属性综合评价系统[J].系统工程理论与实践,1997(9):1-8,42.
[6]程乾生.质量评价的属性数学模型和模糊数学模型[J].数理统计与管理,1997,16(6):18-23.
[7]李光,吴祈宗,齐延信.基于权重稳定区间的综合评价结论一致性研究[J].数学的实践与认识,2010,40(6):54-60.
[8]卢蕊,束永祥,王丽君.数学问题意识、问题提出能力的调查研究[J].镇江高专学报,2007,20(1):96-99.
[9]束永祥,卢蕊.数学问题意识、问题提出的涵义及因素分析[J].镇江高专学报,2005,18(4):105-108.
