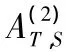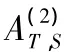分块矩阵的具有指定值域和零空间的外逆的表示

牛含冰

（徐州市第三中学 数学教研室，江苏 徐州 221000）

0 引言

设Cn，Cm×n分别表示复数域上n维向量的全体和复数域上m×n矩阵的全体，‖·‖表示矩阵的谱范数，Ran（·），Ker（·）分别表示矩阵的值域和零空间，I表示适当维数的方阵。

广义逆矩阵在统计学、运筹与控制、神经网络等方面具有重要应用，常见的广义逆有Moore-Penrose广义逆、群逆、Drazin逆、Bott-Duffin逆等［1］。这些广义逆都可以转化为具有指定值域和零空间的外逆（见定义1）［2］。很多学者对具有指定值域和零空间的外逆做了深入研究，取得了很多成果［2-7］。然而关于分块矩阵的具有指定值域和零空间的外逆的研究还不多见。本文对这个问题进行了研究，借助于扰动的方法，给出了2×2的分块矩阵的具有指定值域和零空间的外逆的表示。

1 定义1

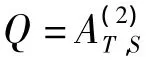
2 引理1

设A，E∈Cm×n=A+E且存在，如果‖‖＜1，则存在，且

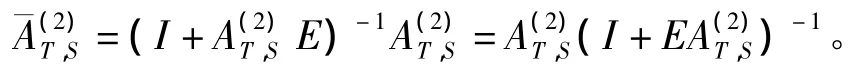
下文中我们记

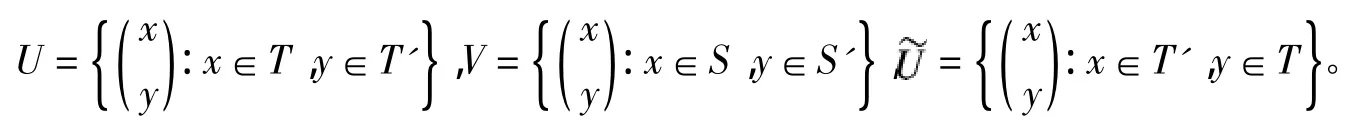
3 定理1

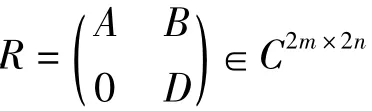
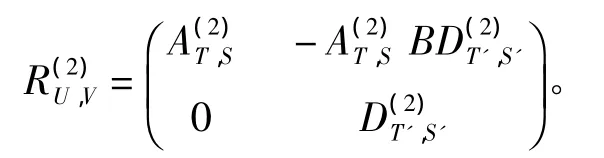
证明 记

则R=M+δM。记

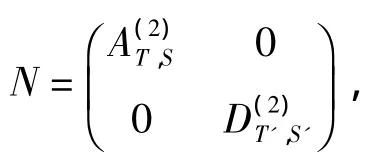
则简单计算知，NMN=N。

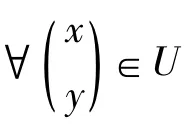
因此，有

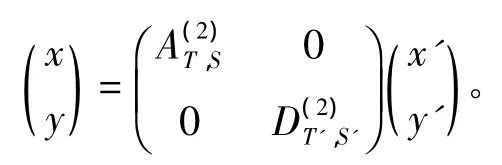
故有U⊆Ran（N）。因此，有Ran（N）=U。

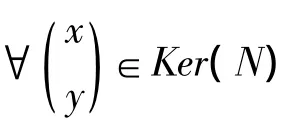
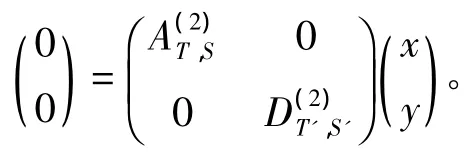
故Ker（N）⊂V。因此，有Ker（N）=V。

注意到

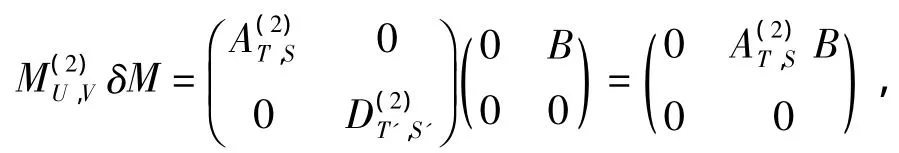
因此

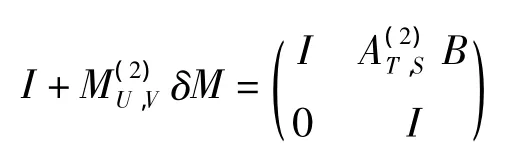
是可逆的，并且

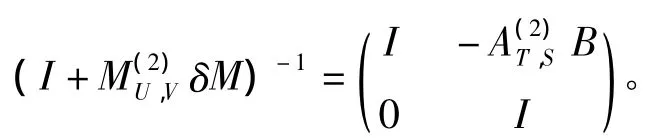
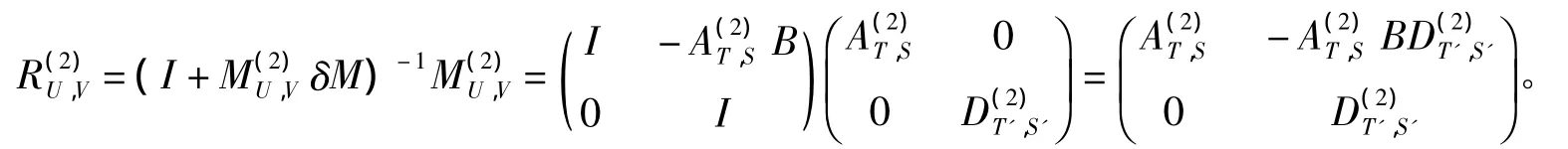
4 定理2

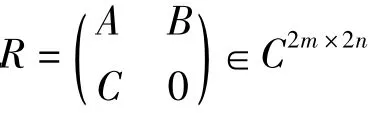
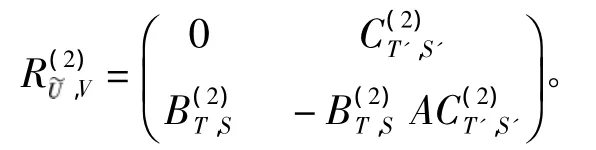
证明 记

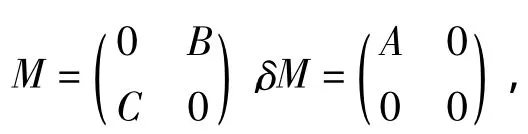
则R=M+δM。

记

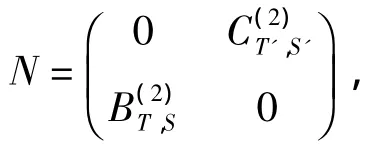
注意到

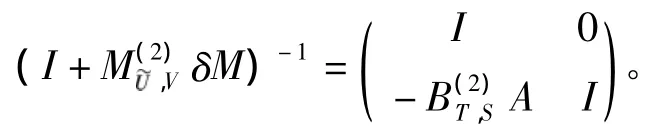
由引理1知

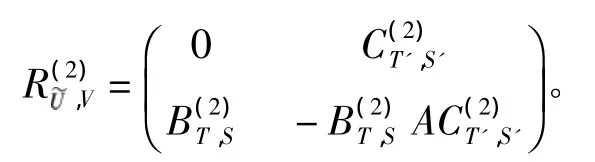
5 定理3

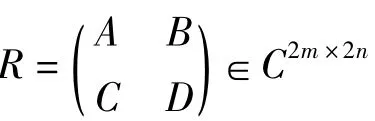
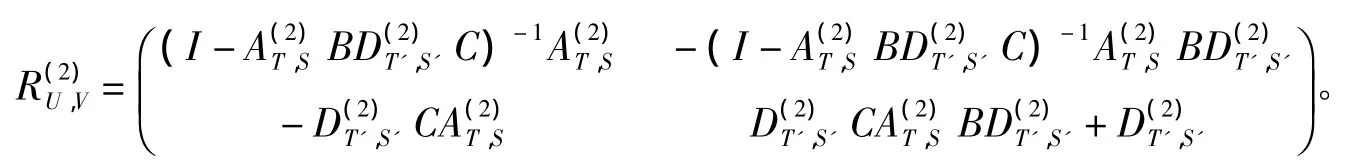
证明 记

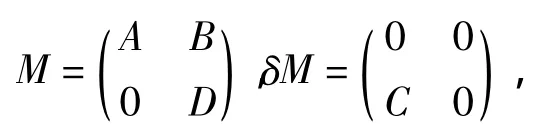
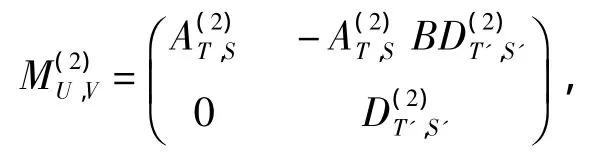
因此

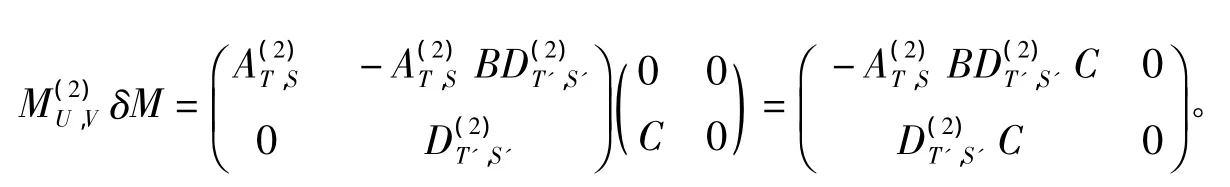
故

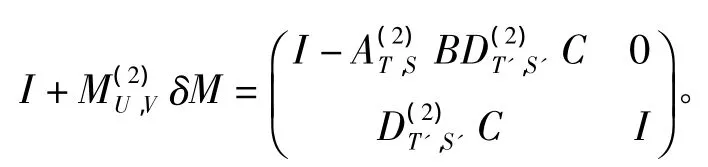
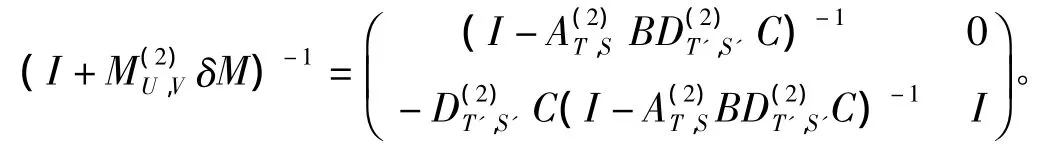
由引理1知

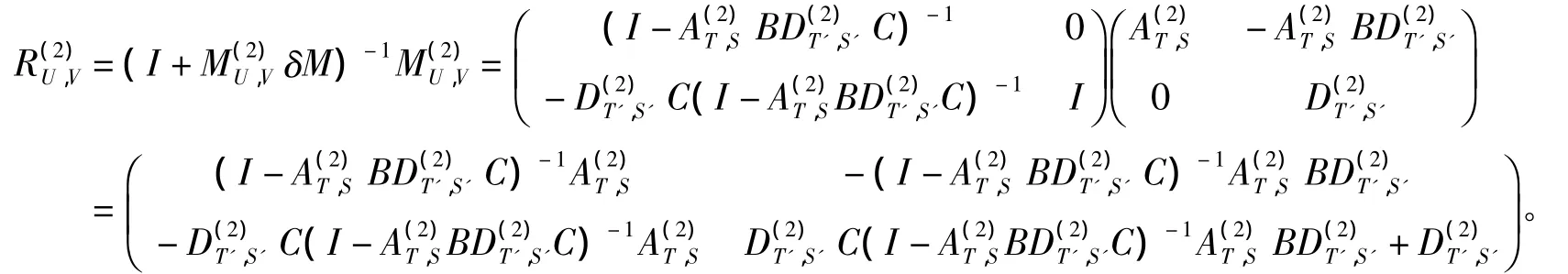
6 定理4

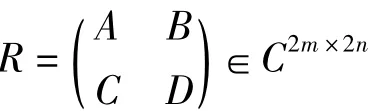
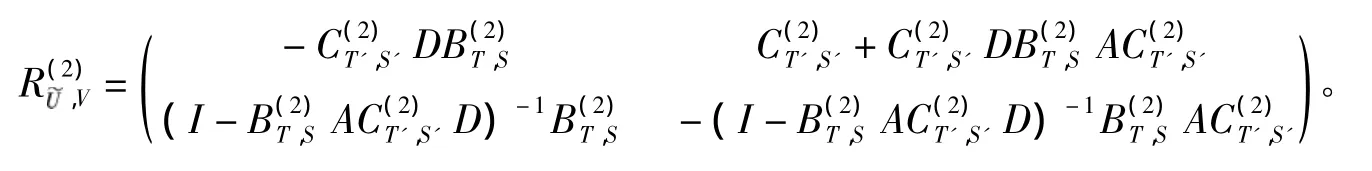
证明 记

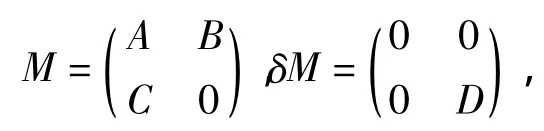
则R=M+δM。

由定理2知

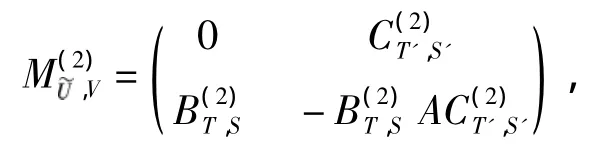
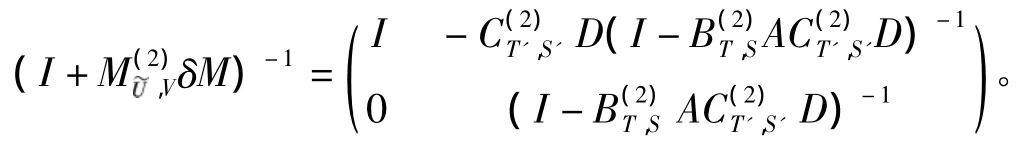
由引理1知

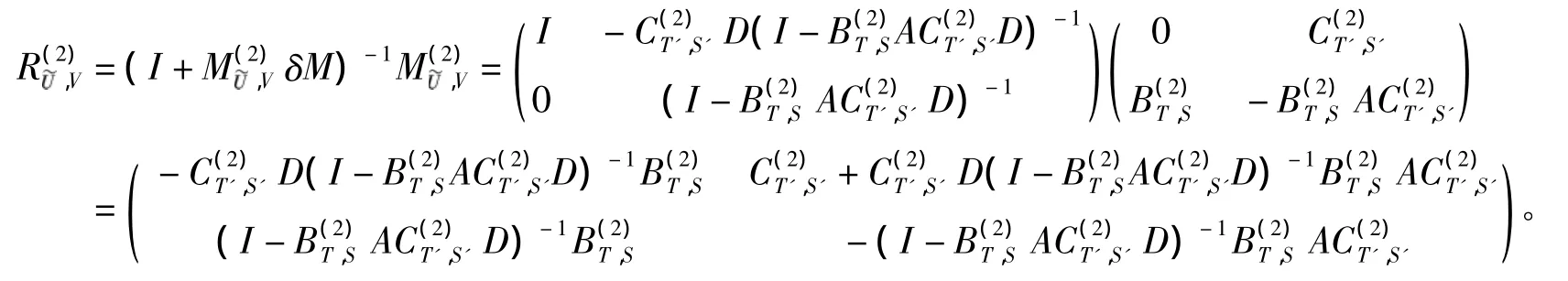
［1］BENISREAL A，GREVILLE T N E.Generalized inverse：Theory and applications［M］.New York：Springer-Verlag，2003.