基于遗传算法的球面阵列旁瓣电平优化方法

张 林，陈客松，邹克利

(电子科技大学电子工程学院，成都 611731)

0 引言

相对于平面阵列，球面阵列可以使载体获得更好的空气动力学性能，所以球面共形阵列在导弹、飞机、卫星等飞行载体中具有重要的运用价值［1］。但是当阵列的孔径很大时，球面上的阵元数就会增加，天线系统的成本也随之增加。为了获得高的空间分辨率和低副瓣特性，同时又降低天线系统的成本，可用稀疏天线单元位置的方法来优化球面天线阵列。稀疏阵中单元的位置一种是完全随机确定，另一种是根据有规则格栅结构确定。随着计算机处理速度的提高，高效稀布阵的设计方法已经受到了很高的重视，并取得了很多研究成果［2，3］，对于复杂的球面阵列的优化研究很少报道，特别是所采用的阵元是有向阵元的情况。

1 建立优化模型

1.1 球面上有向阵元方向图公式的推导

采用对称阵子作为球面阵的基本阵元，假设球面上的对称阵子轴线沿着球的半径方向放置，如图1所示。

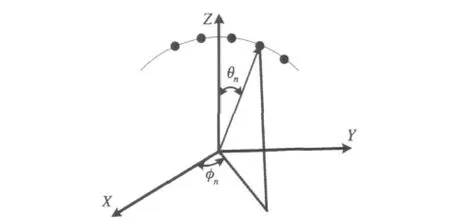
图1 球形阵列坐标系

放置在Z轴上那个阵元的方向图函数为［4］

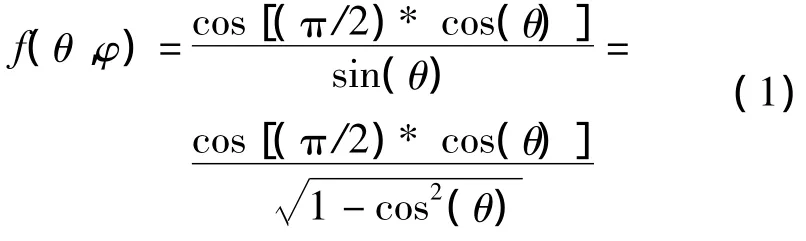
由于采用的是有向阵元，且对称阵子轴向是沿着球面的半径方向，不在Z轴上的阵元的方向图函数不能再用式(1)表达，所以要把每个阵元的方向图都归一化到球坐标系中，方向图推导示意图如图2所示。假设第n个阵元的位置为(R，θn，φn)，借助于图2可以推导出其方向图函数，在推导过程中不考虑阵元之间的互耦合效应及球面对阵元的遮挡效应，球面的背衬是空气。式(1)为cos(θ)的函数，θ为观察方向与天线轴向Z轴的夹角，对应于图2中则为观察方向与的夹角，其远区辐射场电场方向为θ方向，对应图2中的方向。因此计算球面阵的中第n个阵元的方向图，只需计算观察方向与的夹角的余弦，即cos<>，此时阵元方向图可表示为

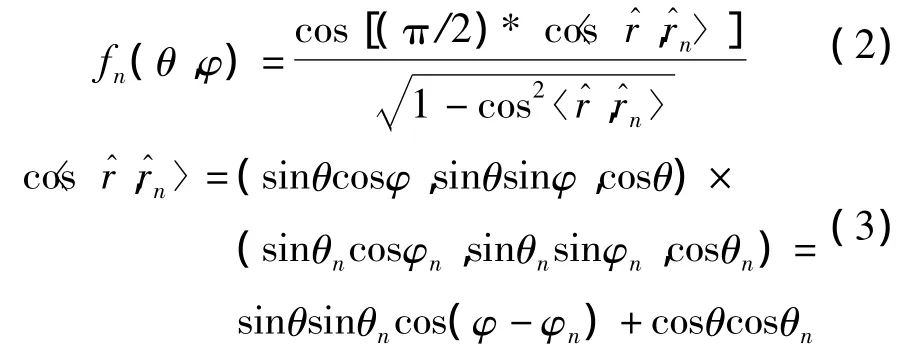
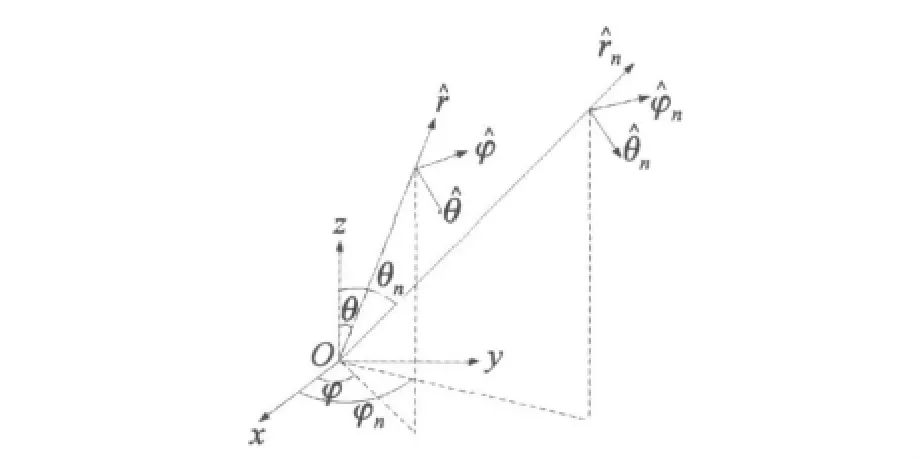
图2 方向图推导示意图

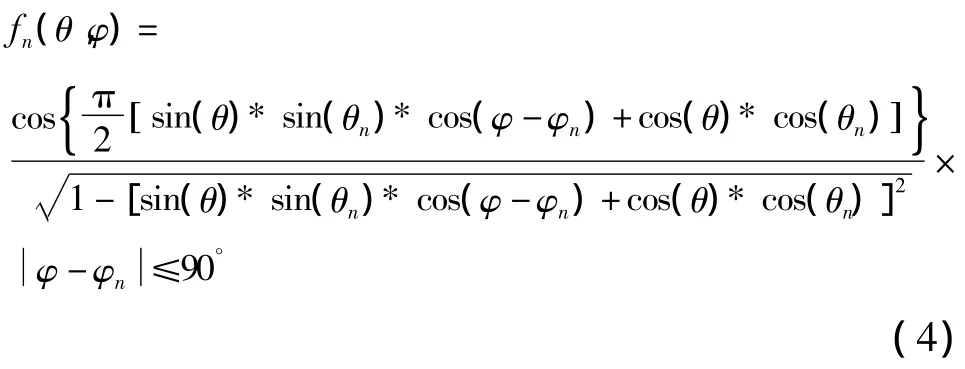
1.2 建立优化模型

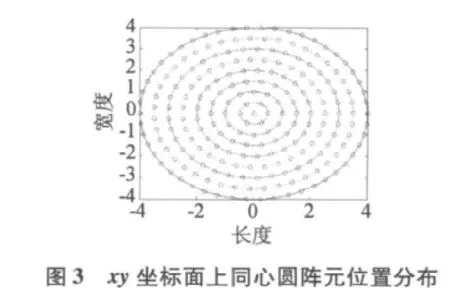
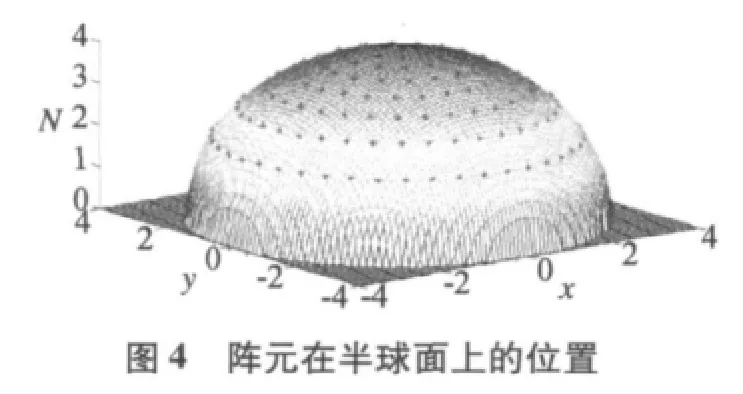
在oxy坐标面上，以原点o为同心圆圆心，半径4λ，相邻圆间距0.5λ，在单元间距d 不小于0.5λ 的条件下，将尽可能多的阵元均匀分布在各个同心圆上。则oxy坐标面上最多可分布的天线单元数为223个，如图3所示，将oxy坐标面上的天线单元向半球面投影后的分布情况如图4所示。

球面阵列方向图函数为可表示为［5］

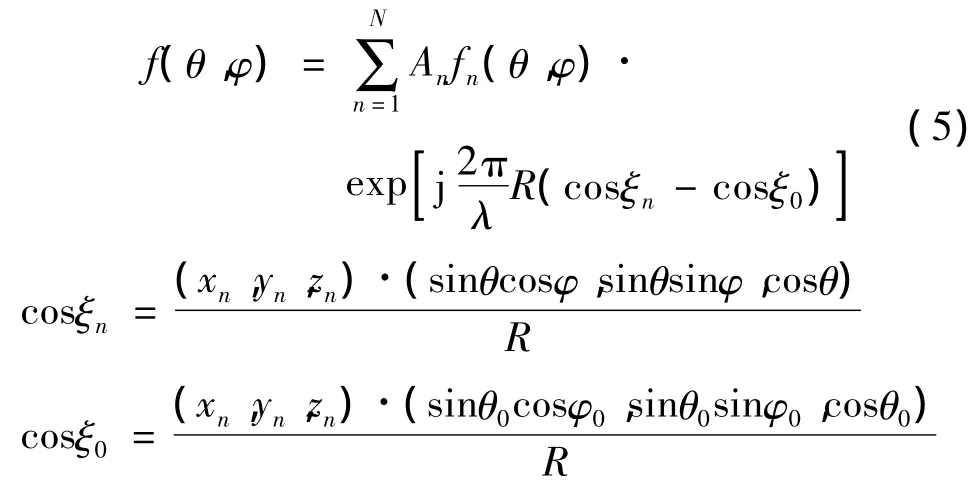
式中，N为天线单元数;An为实数，表示第n个阵元的幅度加权系数，为了简化分析，取An=1;fn(θ，φ)为第n个天线单元的方向图，如式(4)所示;λ为波长;R 为球面半径，R=4λ;(θ0，φ0)为主波束指向;φ是起始于x轴正方向的方位角;θ是起始于z轴正方向的俯仰角;(xn，yn，zn)为第n个天线单元在直角坐标系中的坐标。

进行稀疏后，用xn表示第n个阵元所处的工作状态;xn=1表示第n个阵元在工作;xn=0表示第n个阵元没有工作，即被稀疏掉了，相应的方向图函数为

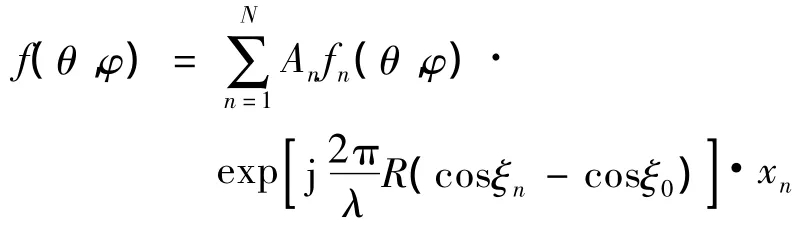
取适应度函数为

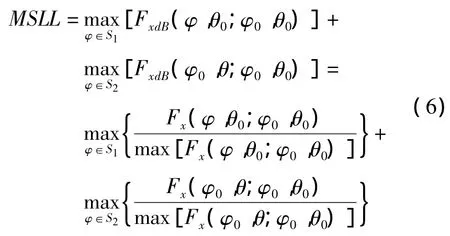
式中，max是求最大值函数;S1是θ=θ0时方向图的旁瓣区域;S2是φ=φ0时方向图的旁瓣区域。可定义如下优化模型

2 遗传算法简介

遗传算法是在20世纪60、70年代由Holland等人提出的一种仿效生物进化与遗传，根据“生存竞争”和“优胜劣汰”原则，通过选择、交叉、变异等算法，使要解决的问题逼近最优解的一种全局概率搜索算法。其主要特点是:使用所求解问题的参数编码形式，而不是使用问题的参数本身，且不要求目标的连续性;从问题空间多点开始搜索问题的解而不是一点。遗传算法在电磁场和微波领域得到广泛应用［6，7］，遗传算法的基本流程如图 5 所示。

6.建立完善环保法律法规和政策措施，增强基层工作的可操作性。地方性政策的制定要建立在符合国家环境保护法律法规的基础上，要对环保工作进行进一步的细化，明确和规范责任，建立和完善促进循环经济发展的法律法规体系和经济政策。开发研究循环经济与生态工业的技术支撑体系。增强规章刚性，全力提高环境执法权威。强化执法责任，建立健全环境执法机制，转变执法指导思想，树立全新环境执法理念，夯实执法基础，有效提升环境执法水平。为环境执法提供依据和政策支持。

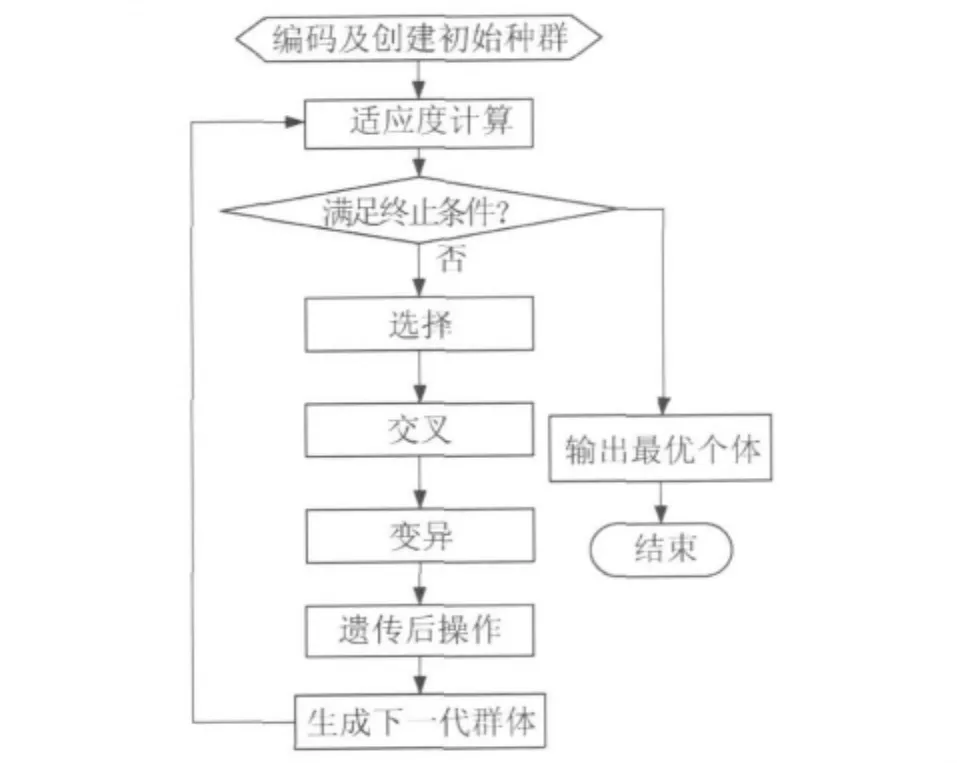
图5 遗传算法流程图

(1)编码

采用P个维数为D，元素仅取0和1的向量作为一个种群，每个染色体表示为

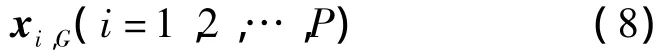
式中，i为染色体在种群中的序列;G为遗传代数;P为种群规模。

由于遗传算法是迭代的优化算法，必须要有搜索的起始点，所以需要对种群进行初始化。初始群体中每个染色体都是随机产生的，如式(9)

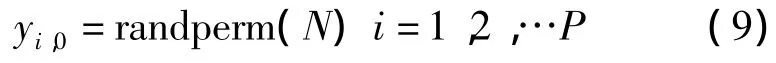
式中，randperm(N)表示将1～N共N个整数随机排列。N为阵元个数，设需要稀疏阵元个数为M个，则取向量yi，0前N－M个值为1，后M个值为0，这就实现了在N个阵元中随机稀疏掉M个，重复P次就可以构成初始群体。

(2)选择

选择就是把原来群体中的染色体按照一定的选择机制进行选择，具体方法是先将群体中的染色体由好到坏排列，序号越小的对应的染色体越好，定义序号i对应的染色体x(:，i)被选中的概率pi为

p是最优染色体被选中的概率，一般来说，取值较大时，尽管优良染色体被选中的机会多，有利于提高收敛速度，但群体缺乏多样性，易造成早期收敛。因此，p的取值不易太大，文中的群体数目为100，通过计算取p=0.05比较合适。再通过旋转赌轮选择染色体，具体过程是:

对每个染色体x(:，i)计算累积概率qi

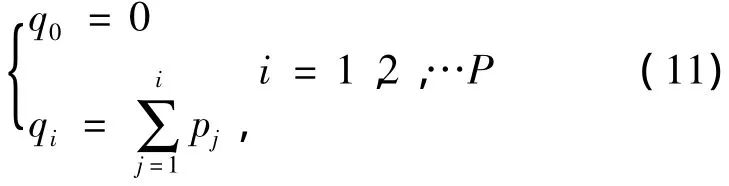
在区间(0，P)内产生均匀分布的随机数r1;若qi－1＜ r1≤qi，则选择第 i个染色体 x(:，i)，(i=1，2，…P);重复进行P次，可得到P个复制的染色体。

(3)交叉

交叉就是选择两个父代，以一定的交叉概率对相应位置上的基因进行交叉，交叉操作过程:把P个染色体分成两组，在每组中选择一个作为父代，在一定的交叉概率下对这两个父代对应位置上的基因进行交叉，如果相等则不进行交叉，从而产生两个新的个体，直到父代所有的染色体都完成交叉。

(4)变异

以变异概率pm在经过交叉的种群中选择进行变异的基因，其过程是从j=1到D，i=1到P，在区间［0，1］中产生一个随机数 r3，如果 r3＜pm，则第(j，i)个基因x(j，i)被选为变异的基因。若被选中的基因值为1，则变为0;为0，则变为1。

(5)遗传后操作

由于在进行交叉和变异后染色体中基因1和0的相对个数可能会发生变化，从而会产生不满足要求的个体，此时就要对这些个体进行一些处理使其满足设定稀疏率的要求。具体方法是:如果个体中0的个数多了，就随机选择多余的值为0的基因，使其为1;如果1的个数多了，则随机选择多余的值为1的基因，使其为0。

通过上面的步骤后就可以得到一个新的种群，从而进行下一次遗传操作。

3 数值仿真

按照之前建立的优化模型，均匀同心圆环共有8层222个阵元(加上圆心处的阵元一共223个，该阵元不参与稀疏优化)，把圆环上的所有阵元投影到半球面上。令波束指向为(180°，45°)，则其方向图如图6所示。

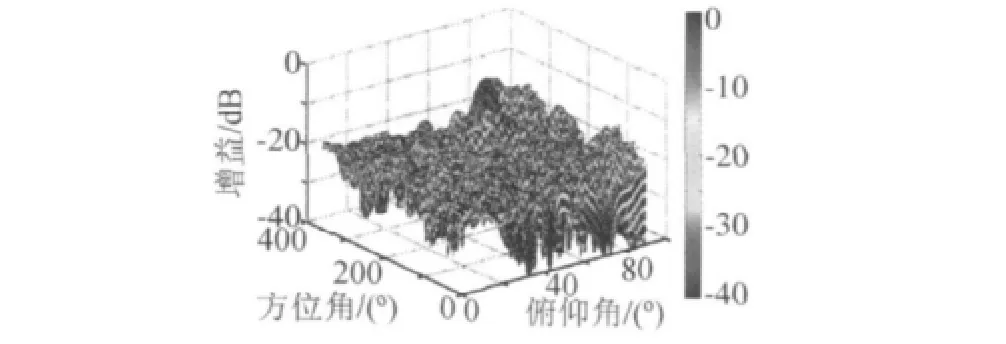
图6 满阵共形球面天线阵方向图

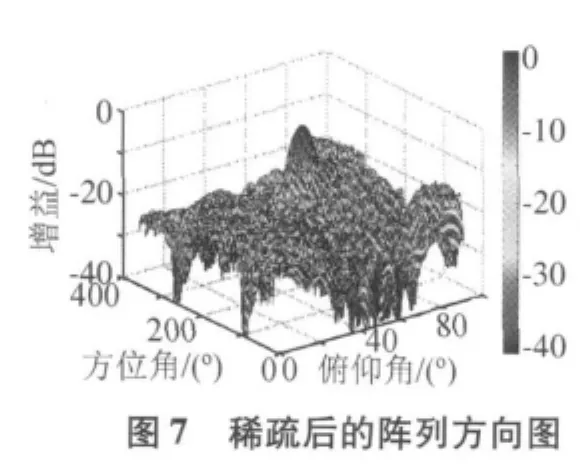
对其进行稀疏个数为M=38个阵元的稀疏。取种群染色体数目P=100，最大遗传代数G=100，变量维数N=222，交叉概率pc=0.6，变异概率pm=0.01，进行5次独立的仿真，对5次独立仿真得到的结果进行统计平均，用统计平均后的数据做相关分析，作出稀疏后的方向图如图7所示。

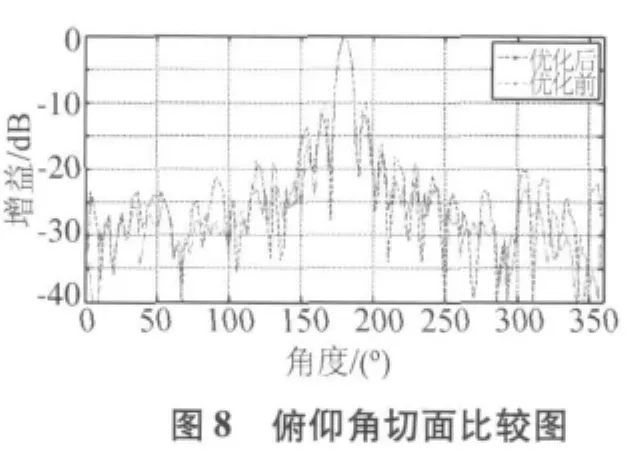
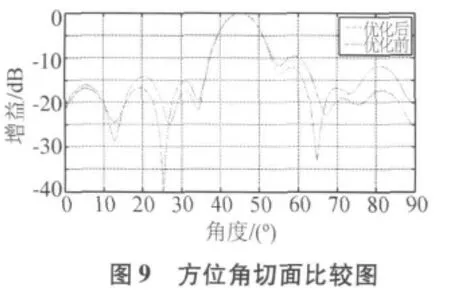
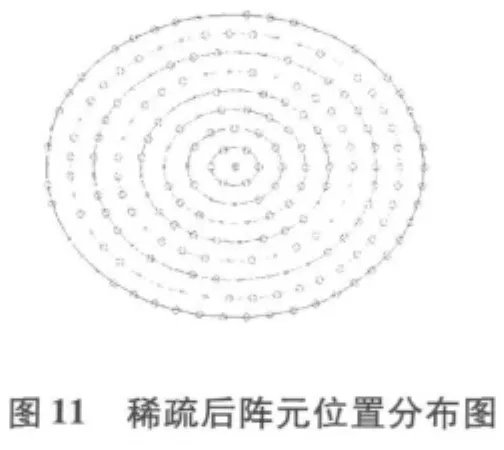
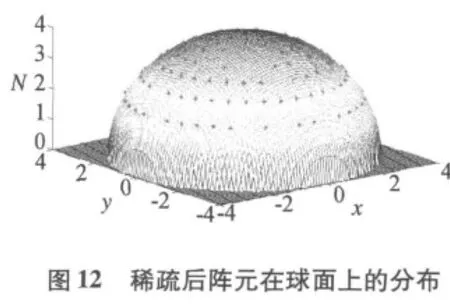
稀疏前(蓝色)和稀疏后(红色)共形球面天线阵列俯仰角切面的比较图和方位角切面的比较图，分别如图8，图9所示。可以看出，稀疏后阵列天线的主瓣宽度保持不变，最大相对旁瓣电平有了降低。其中，俯仰角最大相对旁瓣电平降低1.95 dB，方位角最大相对旁瓣电平降低2.01 dB。适应度函数随遗传代数的变化曲线，如图10所示。在90代以后，适应度函数保持稳定，具有较好的收敛性。稀疏后阵元位置的分布图如图11所示，其中“°”标志的表示该位置有阵元，“×”标志的表示该点的阵元已被优化稀疏，稀疏后阵元在球面上的投影如图12所示。

4 结语

文章针对共形球面阵列天线，采用有向阵元，在经典的遗传算法的基础上进行改进，以降低天线阵列的最大相对旁瓣电平为优化目标，以阵元的工作状态为优化参量对其进行稀疏。仿真表明:该方法可有效降低球面阵列的旁瓣电平，为有关研究提供有益参考。

［1］ ARES F，et al.Synthesis of Antenna Patterns of Circular Arc Arrays［C］//In IEEE Antennas and Propagation Society International Symposium 1997 Digest，1997(4):2248－2251.

［2］ KESONG C，et al.Synthesis of Sparse Planar Arrays Using Modified Real Gennetic Algorithm［J］.Antennas and Propagation，IEEE Transactions，2007，55(4):1067－1073.

［3］ KUMAR B P，BRANNER G R.Generalized Analytical Technique for the Synthesis of Unequally Spaced Arrays with Linear，Planar，Cylindrical or Spherical Geometry［J］.Antennas and Propagation，IEEE Transactions on，2005，53(2):621－634.

［4］ HAUPT R L.Thinned Arrays Using Genetic Algorithms［J］.IEEE Trans.Antennas and Propagation，1994，42(7):993－999.

［5］ YAN K K，LU Y.Side Lobe Reduction in Array－pattern Synthesis Using Genetic Algorithm［J］.IEEE Trans.Antennas and Propation，1997，45(7):1117－1121.

［6］ HAUPT R L.An Introduction to Genetic Algorithms for Electromagnetics［J］.IEEE Antenna Propagat.Mag，1995，37(2):7－15.

［7］ WEI D，MICHIELSSEN E.Genetic Algorithm Optimization Applied to Electromagnetics:A review［J］.IEEE Trans，1997，AP－45(3):343－353.