前方交会放样精度与图形关系的探讨

李琪

1 概述

随着科学技术的发展及测绘仪器的更新，测量并不局限于某一种单一的方法，但传统前方交会方法，由于其原理简单、施工方便、对测绘仪器要求不高等特点，至今仍在地形图测绘、工程施工等环节中被经常使用。尢其是人们在一些无法到达或无法安置仪器的地方进行测量和施工时，或图根锁或经纬仪导线测量的方法布设的图根控制点，尚不能满足大比例尺测图需要时。因此，研究前方交会方法所得点位的精度及其精度提高措施是非常必要的。本文推导前方交会点位放样精度的计算，并对角度交会、距离交会进行了比较，总结了利用前方交会法进行施工放样时应注意的问题。

2 角度前方交会

2.1 角度交会原理

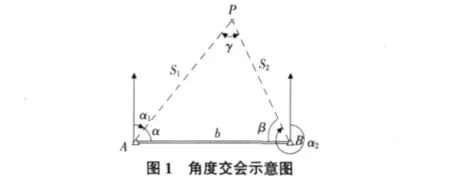
角度交会法又称为方向交会法，在量距不方便的场合，角度交会是放样比较常用的方法。如图1所示，A，B为两已知控制点，P点为待放样点，根据A，B，P三点的坐标，可以反算出两个交会角α，β，现场放样时，在已知点A，B上架设两台经纬仪，分别放样相应的角度就能确定待放点P的平面位置。为提高精度，可采用三方向交会，产生示误三角形，取重心或将一角点投影到对应方向上以其垂足作为最后点位。精密放样时，采用角差图解法，主要适用于动态和快速定位。

放样角元素计算:

放样元素检查:

2.2 角度交会精度分析

设两角度的放样精度相同，均为mβ，对于角度交会法误差椭圆可知:

其中，γ为交会角度;u，v分别为角度α，β放样误差所引起的点位误差的影响;P点放样点位误差M可用下式表示:

其中，b为已经控制点A，B两点的距离。

现做以下讨论:

当b为定值时，且当交会角γ一定时，M只与α，β有关，在M计算式中，与α，β的内容可以用函数y表示如下:

为求函数y的极值，需对y求一阶导:

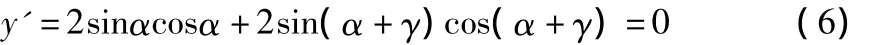
当α=β时，即对称交会时，M有极值。

为进一步确定是极大值还是极小值，对函数y求二阶导:

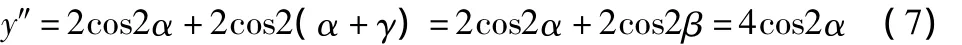
当y″≠0时，该函数才有极值:

1)γ＞90°时，2β为锐角，y″＞0，y极小，对称交会最有利;2)γ= 90°时，β=45°，cos2β=0，y″=0，y'=0，y无极值;3)γ＜90°时，2β为钝角，y″＜0，y极大，对称交会最不利。

3 距离前方交会

3.1 距离交会原理

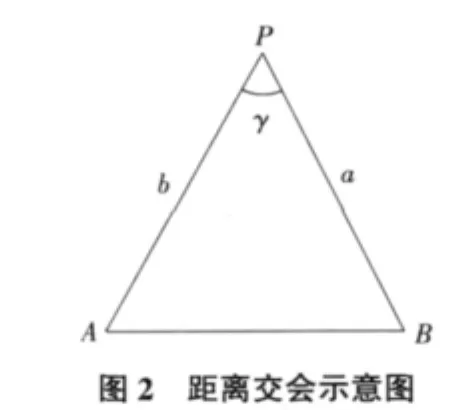
距离交会是前方交会的一种，操作方便，原理简单，特别是在地势比较开阔的时候。如图2所示，A，B为两已知控制点，P点为待放样点，根据A，B，P三点的坐标，可以反算出已知控制点A，B距离待定点P之间的距离a，b。现场放样时，分别以A，B为圆心，用钢尺或测距仪以相应的距离为半径作圆弧，两圆弧的交点即为待定点的平面位置。

3.2 距离交会精度分析

设边长a，b的放样精度分别为ma，mb，根据距离交会误差椭圆可知，由ma，mb所引起的放样点位的误差分别为:

其中，γ为交会角度;u，v分别为距离放样误差所引起的点位误差，最终P点放样点位误差M可用下式表示:

4 角度交会与距离交会的对比

通过对角度交会、距离交会放样法的了解及精度分析，现对两种方法放样点位的误差椭圆进行比较分析，见图3，其中，实线为角度交会放样的点位误差椭圆，虚线为距离交会放样的点位误差椭圆。

由图3可知，角度交会与距离交会误差椭圆在精度匹配时，长轴方向相差90°。在交会角γ=90°时，两椭圆重合。在同等环境下，通常来说，采用距离交会与角度交会放样得到的点位精度是不一致的，因此交会方法的选择应结合实际情况进行:

1)当交会角度γ为钝角时，角度放样的点位在纵向误差较小，距离放样的点位在横向误差较小;2)当交会角度γ为锐角时，角度放样的点位在横向误差较小，距离放样的点位在纵向误差较小;3)当交会角度γ为直角时，放样点的精度与方法的选择无关。

5 结语

当采用前方交会法进行放样时，应根据实际施工环境、工程本身的要求进行放样方法选择:1)当交会角为钝角时，角度交会在纵向误差较小，距离交会在横向误差较小;2)当交会角为锐角时，角度交会在横向误差较小，距离交会在纵向误差较小;3)当交会角为直角时，可以采用距离交会或角度交会。当受环境影响，只能采用角度交会方法进行点位放样时，应尽量使得交会角γ为钝角，且采用对称交会;尽量避免γ为锐角时的对称交会。

［1］ 王德修.矿区地形测量［M］.北京:煤炭工业出版社，1993.

［2］ 高井祥.测量学［M］.徐州:中国矿业大学出版社，2002.

［3］ 李青岳.工程测量学［M］.北京:测绘出版社，2008.

［4］ 徐亚军.高速铁路施工放样测量的方法与研究［J］.山西建筑，2010，36(13):345-346.