箱梁翼缘板的合理设计分析
2011-04-14杨立坤赵传亮
杨立坤 赵传亮
0 引言
随着我国桥梁建设事业的快速发展,大跨度箱梁使用的越来越多,悬臂长度超过3 m的大悬臂混凝土箱梁也在大跨度连续梁、连续刚构桥中广泛应用。但一直以来,箱梁悬臂板的计算都很少有人重视,通常我们都参照JTG D62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范(下称“规范”)中的规定进行分析计算,但《规范》中对于翼缘板的假设过于简单,在某些情况下会偏于危险,而且没有考虑到当车辆荷载作用到箱梁端部悬臂上悬臂板的半无限效应。为了安全合理的设计桥梁,悬臂板的计算也应该给予足够的重视。
1 理论分析
对于无限宽等厚悬臂板,在自由端作用一集中荷载时,通过理论分析可以得到:
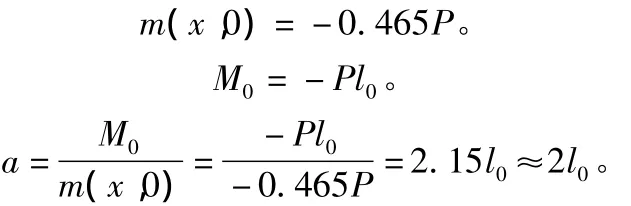
其中,m(x,0)为无限宽度悬臂板根部单位宽度上的弯矩;M0为断臂根部总弯矩;l0为悬臂板跨径;a为荷载有效分布宽度。
上面就是《规范》中悬臂板计算公式的由来。可见规范中悬臂板的计算是基于无限宽等厚悬臂板,在悬臂端部作用一个集中荷载的情况推导出来的。从结构计算方法来看,有效分布宽度的概念是将板简化成梁来计算,优点是较为简单实用,但其掩盖了板的双向受力的特性。1971年,英国利物浦大学沙柯(Sanko F.)等人研究并与众多学者的研究分析比较之后提出了如下的实用计算公式:
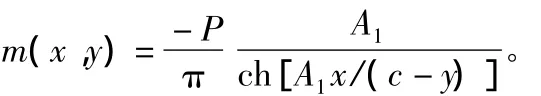
其中,m(x,y)为板内(x,y)点的弯矩;c为荷载作用点离根部距离;l0为悬臂板长;A1为与计算点、板厚比等有关的参数。
对于半无限板的情况,加拿大的Bakht.B给出了当集中荷载位于悬臂行车道板横向自由边缘附近时的悬臂根部弯矩[1]。悬臂板根部弯矩对于跨中和梁端的差异,国内也做过类似的分析和实验。2003年王健等人选取了两根20 m长,悬臂长度分别为1.2 m和2.0 m的T形边梁进行了现场荷载实验,实验结果表明,梁端弯矩是跨中弯矩的1.6倍左右[2]。1988年同济大学研究生蒋志刚同志也进行了有机玻璃箱梁模型验证,并指出当荷载作用于距箱梁端部3倍的悬臂板跨径范围内时,应该按半无限悬臂板计算[3]。
2 力学分析
本文使用有限元软件ANSYS进行建模分析,首先对不同悬臂长度,不同集中荷载作用位置,不同板根与板端厚度比的根部固结的悬臂板进行分析,并与规范和Sanko公式对比,结果见表1。
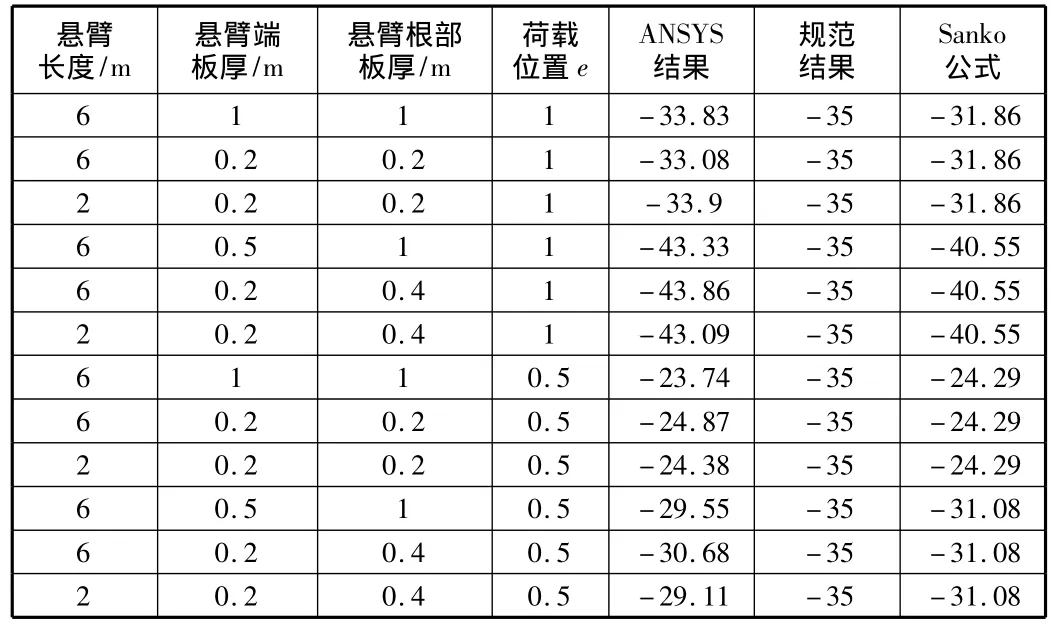
表1 集中荷载计算结果
表1中数据为单个车轮荷载(70 kN)作用下,悬臂根部的最大弯矩,可以看出,ANSYS计算结果和Sanko公式计算的结果一致性比较好,从结果可以看到板的根部与端部的厚度比越大,荷载越靠近悬臂端部,悬臂根部弯矩就越大,而《规范》的公式却没有体现出这种规律,由表1可以看到,当板根部与端部的厚度比为2,荷载作用于悬臂端部的时候,按《规范》计算的结果就偏于不安全了。
表1的计算是基于集中荷载,且有荷载作用于板悬臂端,而实际中,车轮都是具有一定面积的分布荷载,且与悬臂端部有一定距离。因此选取了某悬臂长4.5 m的箱梁桥进行计算,悬臂端部板厚0.2 m,悬臂根部0.8 m。桥面铺装0.2 m,车轮荷载按45°角扩散到桥面板上,车轮荷载中心距离悬臂端1 m。纵向自梁端开始以1 m步长向跨中移动,并与同尺寸悬臂板计算及Sanko公式计算结果对比,结果见表2。
从表2中可以明显看到,当车轮作用在远离梁端时,即满足无限长悬臂板的假设时,悬臂根部固结模型与以根部固结假设为基础的Sanko公式的结果分别为41.46和42.36比较接近,而全箱梁模型的计算结果为30.9左右,要小25%左右,这是因为全箱梁模型中箱梁会由于车轮荷载产生变形,使箱梁翼缘板的根部弯矩分布更加均匀。这也与蒋志刚的研究结论相近[4]。《规范》计算结果为28.33,比有根部固结模型的有限元结果偏小32%,与考虑了箱体变形对悬臂根部弯矩释放的全箱梁模型相比,也偏小8.3%,这在设计中是不安全的。而且箱体变形对翼缘板根部弯矩释放作用的大小不经过详细的计算很难确定。蒋志刚同志在其硕士论文中提出了近似的计算方法[3]。
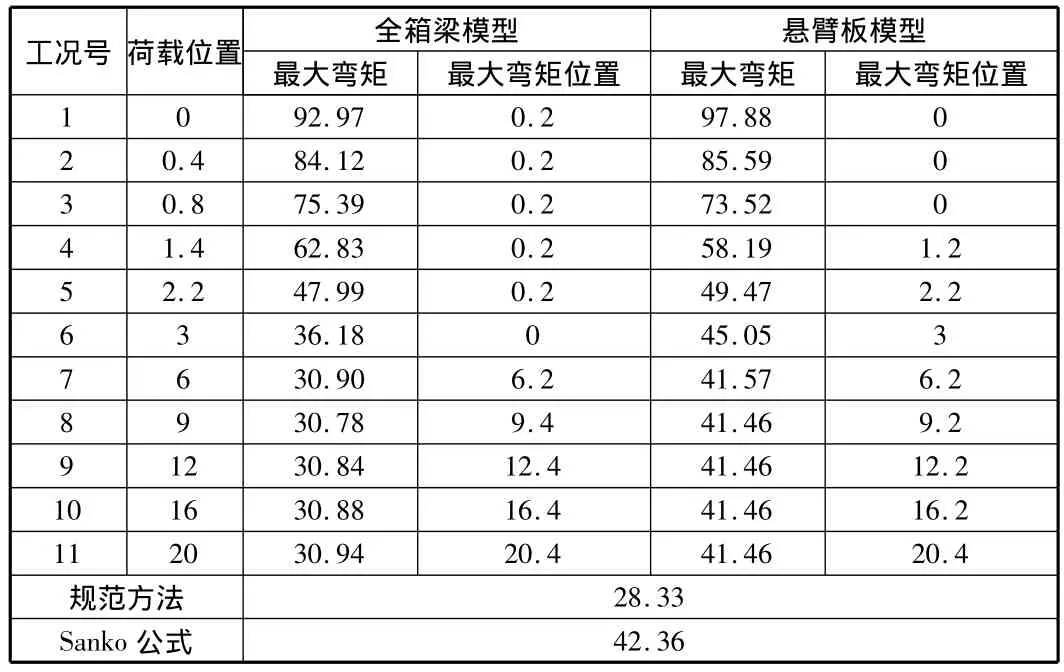
表2 单车轮计算结果
从上面的计算中同样可以看到,当车轮荷载作用于箱梁端部附近的翼缘板上时,翼缘板的半无限板效应明显。在全箱梁模型中,近自由端的悬臂根部弯矩是跨中悬臂根部弯矩的3倍;在悬臂板模型中,近自由端的悬臂根部弯矩是跨中悬臂根部弯矩的2.36倍,所以实际设计中应该对此加以注意。但这种效应也是有一定范围的,当荷载作用在距自由端1倍悬臂长度以外时,翼缘板的根部弯矩就十分接近于荷载作用于跨中了。
3 结语
本文针对不同的荷载状态,对全箱梁模型和悬臂板模型的翼缘板根部弯矩进行分析得出:
1)对于翼缘板根部与端部的厚度比较大且荷载作用于翼缘板跨径端部的时候,《规范》对于悬臂板根部弯矩的计算可能偏于危险,要加以注意。
2)荷载位置靠近箱梁端部时,翼缘板根部弯矩的集中效应明显,对于全箱梁模型,箱梁端部翼缘板根部弯矩可达跨中的3倍以上。对于悬臂板模型,箱梁端部翼缘板根部弯矩为跨中的2.4倍左右。翼缘板根部弯矩在箱梁端部附近的集中现象在距离箱梁端部1倍悬臂长度范围内比较明显,此范围以外就已经和跨中的翼缘板根部弯矩相差无几了。
当翼缘板根部与端部的厚度比较大且荷载作用于翼缘板跨径端部的时候,悬臂板配筋要详细分析计算,当荷载的作用点离自由端一定距离时,在作用点位置处也会产生正弯矩,因此要求在板的下缘配置足够数量的钢筋。由于翼缘板根部弯矩在箱梁端部附近的集中现象,在实际设计中应该把距离箱梁自由端1倍悬臂长度范围内的荷载放大或者把这部分的钢筋进行加强。如缺乏详细计算结果,不妨参考日本或者加拿大规范。
[1] 张士铎.悬臂行车道板计算理论综述[J].重庆交通学院学报,1992,11(2):23-34.
[2] 王 健,刘庆仁.桥梁悬臂板结构受力分析和探讨[J].公路,2003(4):21-24.
[3] 蒋志刚.单箱脊骨梁桥悬臂行车道板理论与试验研究[D].上海:同济大学硕士研究生论文,1988.
[4] 蒋志刚.大伸臂箱梁桥横向弯矩研究[J].华东公路,1994 (6):26-27.
