叶栅内非定常流动特性的频谱分析

李少华, 王梅丽, 杜利梅, 郭婷婷

(1.东北电力大学 能源与动力工程学院,吉林 132012;2.北京国电龙源环保工程有限公司,北京 100052)

动静叶栅内部存在较强的尾迹涡.尾迹涡不仅对下游叶栅周围的流动、传热等特性产生较大影响,同时也会造成叶栅内的能量损失.因此,进行静叶尾迹涡方面的研究对叶轮机械的优化设计具有重要意义.

目前,科研人员对叶栅内尾迹涡的研究已经取得了一些成果.A.K.Sinha[1]采用热电偶对不同密度比下的气膜冷却进行了试验研究,发现随着主流与射流密度比的增加,冷却效率逐渐提高.A.B.Mehendale[2]利用轮辐式尾迹发生器模拟尾迹,研究了非定常尾流对下游流场以及传热的影响.G.J.Walker[3]和H.Pfeil等[4]采用热线风速仪对压气机叶片边界层进行试验研究后发现:非定常流动强烈影响叶栅通道中的能量传递.

在数值模拟方面,D.L.Sondak等[5]是最早利用数值模拟方法对一级涡轮叶栅进行分析的科研人员.他利用傅里叶变换分析了尾迹涡的脱落频率,并得出涡的脱落主要是由于动静叶相互运动产生的非定常效应.M.M ocazala等[6]利用数值方法对轴流涡轮叶片损失进行了分析,结果表明:导致涡轮叶片损失的关键因素是尾迹和势流.郭婷婷等[7]对扇形喷孔进行了大涡模拟,并通过对涡的流动机理进行分析,得到了涡的脱落周期以及涡脱落的特点.李少华等[8]采用数值模拟方法研究了复合角度对叶片冷却效率的影响,结果表明:相同复合角度、不同吹风比的压力面和吸力面冷却效率变化一致,而不同复合角度对气膜冷却效率影响较大.袁锋等[9]模拟了静止与旋转工况下的三维流场,并研究了涡轮内部三维流场的速度变化.

在涡轮叶栅中,由于尾迹涡的脱落,存在分离现象,严重影响涡轮叶片的气动性能,但目前国内对尾迹涡脱落问题的研究甚少,尚处于起步阶段.笔者利用数值计算研究并分析了尾迹涡的脱落频率及其对能量损失的影响.

1 物理模型和数值计算方法

1.1 物理模型与网格划分

本文采用某轴流透平中截面的型面坐标.图1为动静叶片的物理模型.表1为动静叶片物理模型的主要参数.计算区域包括动静叶栅两个部分.在实际中,动静叶片的数目不等,为提高效率,对原始模型叶片数进行了简化,假设静叶数和动叶数之比为1∶1,各有 60个叶片.整级叶栅的内径为2 005 mm,外径为 2 295 mm.静叶轴向弦长 Cx=150 mm,动叶轴向弦长Cy=200 mm,动静叶之间的轴向间距为20%Cy.

图1 动静叶片的物理模型(单位:mm)Fig.1 Physicalm odel of stato r vane and rotor b lade(unit:mm)

表1 动静叶片物理模型的主要参数Tab.1 Main parameters of physicalmodels for stator vaneand rotor blade

由于模型比较复杂,对整级叶栅进行了网格划分.但由于网格结构的数量庞大,难以进行数值计算,因此采用周期性边界条件,动静叶交界面采用滑移网格技术,以便使交界面上的数据能有效传递.采用连续界面法[10]实现网格界面上的数据传递,计算网格采用非结构六面体网格,叶栅通道网格示于图2.

图2 叶栅通道网格Fig.2 Grid division of cascade channel

1.2 数学模型

选取空气为流动介质,设流动为不可压缩流动,通用控制方程为:

式中:φ为广义变量;Γ为相应于φ的广义扩散系数;S为与φ对应的广义源项,在源项S中考虑了离心力、哥氏力和浮升力的影响.

采用SST k-ω湍流模型进行数值模拟.k-ω湍流模型是基于湍流动能输运k和大尺度湍流频率ω的方程模型,该模型中k和ω的输运方程为:

式中:Gk为湍动能;Gω为ω方程;Dω为正交发散项;Γk、Γω分别为k 与ω的有效扩散项;Yk、Yω分别为k与ω的发散项;Sk和Sω分别为用户自定义项.

1.3 数值计算方法

通过求解非稳态不可压缩N-S时均方程进行计算,紊流模型采用SST k-ω湍流模型,通用控制方程的离散采用有限容积法,控制容积界面的物理量采用二阶迎风格式,流体压力-速度耦合基于Simp le算法,并将定常解作为非定常求解的初场以加速收敛.在计算过程中,能量方程的收敛精度取10-6,其他方程的收敛精度取10-3,残差曲线满足精度表明计算收敛.

1.4 边界条件

进出口边界条件:进口总压为101.325 kPa,总温为300 K,出口静压为97.576 kPa,在数值模拟中,将定常解作为非定常求解的初场.

周期性边界条件:静叶与动叶栅距相等.每一时刻静叶通道下边界与上边界满足周期性边界条件

式中:ps为静叶栅距.

动静叶相关边界条件的处理:由于叶排间的相对转动,使每排叶栅的交界面上的参数随时间不断变化,进而使流场呈现周期性的变化规律,本文采用滑移面法[11],静叶区和动叶区之间的数据传递在滑移面处通过插值进行,能较好地实现数据的传递.

2 结果与分析

2.1 计算结果分析

计算经过17个周期后,监测得到的进出口流量以及升力等参数都达到了良好的周期性,且残差曲线满足精度,据此可认为非定常数值模拟的结果已收敛.图3为动叶表面升力系数随物理时间推进的监测曲线,其中轴向间距为20%Cy,转速为500 r/min.笔者定义时均误差为非定常计算在几个周期内误差的平均值,非定常数值模拟所得到的进出口质量流量的时均误差为0.03%,在0.5%之内,表明该计算结果是可靠的.

动叶表面受到流体升力阻力作用的原因有两方面:一是流体中的紊流随机脉动,因其幅值较小,没有固定的变化周期;二是由静叶尾部旋涡周期性地交替脱落而产生涡街引起的,其幅值较大,且在一定条件下会形成稳定的变化周期,因此可认为:由升力系数及阻力系数变化曲线经FFT变换后得到的功率谱图上的峰值所对应的频率就是旋涡脱落的频率.功率谱密度图的横坐标是频率,纵坐标为自功率谱密度(PSD)函数,其物理含义就是单位频带所具有的平均能量.由于旋涡运动会产生熵增,从流场中熵的瞬时分布可以看出旋涡的特征,并可以清晰地看到非定常流场的发展和旋涡结构以及气流的分离和涡的生成、脱落过程.

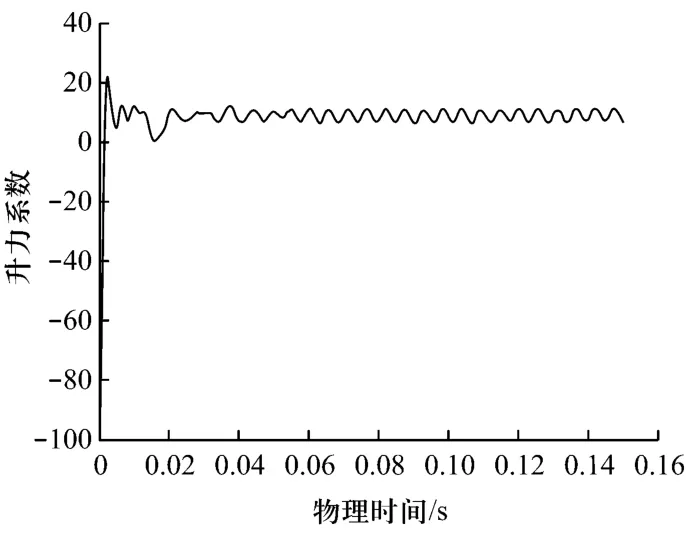
图3 动叶表面升力系数随物理时间推进的监测曲线Fig.3 Cu rve of blade su rface life coefficient varying with physical time

2.2 不同轴向间距的频谱分析图

图4为不同轴向间距的动叶表面升力系数和阻力系数频谱分析,其中转速为500 r/min.由图4可知:功率谱图上存在明显的峰值,表明此频率处功率谱能量很集中.此时,旋涡的脱落具有明显的周期性特征,且旋涡能量较大,有稳定的涡街存在.通过频谱分析可知:当轴向间距为20%Cy时,功率谱密度峰值较高,这是由于轴向间距较小时,尾迹在进入下游通道前与主流还未完全掺混,轴向的不均匀性引起动叶表面边界层剧烈扰动,导致动叶周围能量较高.随着轴向间距的增大,尾迹逐渐与主流掺混,消除了气流沿轴向的不均匀性,使尾迹传播到动叶,衰减增大,降低了能量损失,进而随着轴向间距的增大,功率谱能量逐渐减小.涡脱落实际上是静叶尾缘边界层将邻近物面的涡量向流体内部输运的结果,即静叶尾缘边界层发展与尾迹旋涡的产生有很大关系,轴向间距的改变减小了气流的扰动,但对静叶尾迹边界层的影响并不明显.因此,在3种轴向间距下,涡脱落的频率差异很小.

图4 不同轴向间距的动叶表面升力系数和阻力系数的频谱分析Fig.4 Spectrum analysis of blade surface life and drag coefficien t varying w ith axial spacing

2.3 不同轴向间距的流场瞬时等熵图

图5为不同轴向间距下50%叶高处动叶瞬时等熵图.从图5可知:当尾迹涡发生脱落时,它会与周围的流体发生强烈的相互作用,并会在对侧的剪切层中形成高压区,从而使其对侧的剪切层形成集中涡,同时所形成的高压区还会影响动叶附面层的流动,使得尾迹中气流的熵值明显比主气流区内大.在吸力面上前缘处,熵值增加很快,这是由于动叶吸力面的强逆压梯度使得尾迹运动到吸力面前缘发生分离,造成熵值的增大,从而导致大量的能量损失.

从图5可知:当轴向间距为20%Cy时,动叶周围流场熵值较大,随着轴向间距的增大,动叶周围流场的熵值逐渐变小,这是由于轴向间距越小,叶片周围的轴向不均匀性越大,剧烈扰动带来的能量损失就越大.当轴向间距增大到100%Cy时,由于气流的掺混作用,在动叶的进口处气流已经接近均匀,静叶尾迹传播到动叶的衰减增大,故损失的能量减小,熵值就变小,这进一步证明了频谱分析的结果.

图5 不同轴向间距下50%叶高处动叶瞬时等熵图(w=500 r/m in)Fig.5 50%height instantaneous en tropy of bladew ith different axial spacing(w=500 r/min)

2.4 不同转速下的频谱分析图

图6为不同转速下动叶表面升力系数与阻力系数的频谱分析.从图6可知:在不同转速下,动叶表面的脉动升力功率谱都存在明显的峰值,这表明3个转速下动叶表面均存在稳定的旋涡脱落现象.通过频谱分析可知,在500 r/m in时的功率谱峰值能量较小,尾迹涡脱落频率较小,而在1 000 r/min和2 000 r/min时的功率谱峰值能量较大,尾迹涡脱落频率也较大.这是因为低转速时主要受到哥氏力的作用,而当转速达到1 000 r/m in时,不仅受到哥氏力作用,而且还受到较强的离心力作用.这时,由于离心力的作用,尾迹周期性的瞬时脉动梯度给边界层的流体注入了高能量.转速越大,动叶切割尾迹的速度越快,注入的能量就越多,从而导致高转速工况下功率谱能量更大.同时,转速的增加也导致能量的频带加宽,这是由于在低转速时,流体流动相对稳定,对旋涡干扰小,能量频带比较集中;当转速增大时,流体湍流强度增加,尾迹带来的高湍流强度加快了尾迹涡的脱落频率,而剧烈的扰动促使旋涡由层流逐渐过渡到湍流,从而导致高转速下出现了宽频带.

图6 不同转速下动叶表面升力系数和阻力系数的频谱分析Fig.6 Spectrum analysis of blade su rface life and drag coefficien t varying w ith rotor speed

2.5 不同转速下的流场瞬时等熵图

图7为 20%Cy轴向间距、50%叶高、不同转速下动叶流场的瞬时等熵图,从图中可以清晰地看到尾迹涡的产生和脱落过程.从图7可知:随着转速的增加,动叶表面的熵值逐渐增大,这是由于转速增加促使尾迹被动叶切割后其迁移速度不断加快和尺度沿流向不断增加,进而使旋涡的诱导作用增强.在高转速下,旋涡便将周围的主流携带进入和穿越尾迹,从而导致动叶周围的能量损失较多.图7(a)中尾迹的脱落形成了明显的旋涡,而图7(b)和图7(c)中的旋涡则发生了明显破碎现象,这主要是由于转速的增加使离心力的不稳定性增加,旋涡的压力分布不足以平衡旋涡上流体质点受到扰动后离心力的变化.当转速较高时,高强度的旋涡失稳破碎后会与周围流体发生相互作用,引起边界层的强烈扰动,造成熵值增大,导致较大的能量损失.由于动叶吸力面强逆压梯度的作用,在吸力面前缘发生分离,并在对侧压力面的剪切层中形成高压区,进而使压力面剪切层形成集中涡,造成压力面的熵值大于吸力面.同时,由于叶背和叶盆上存在压差,在叶片表面附面层内压力梯度的影响下,尾迹将被挤压到吸力面一侧,并与吸力面的附面层发生复杂的相互作用.

图7 20%Cy轴向间距、50%叶高、不同转速下的动叶瞬时等熵图Fig.7 Instantaneous entropy for 20%Cy axial spacing,50%blade height and different rotor speed s

3 结 论

(1)动静叶之间轴向间距越小,周向的不均匀性越大,叶栅通道中熵值就越大.随着轴向间距的增大,对尾迹涡脱落频率影响不大,但流场中熵值却逐渐变小,叶栅通道中的能量损失逐渐减小.

(2)随着转速的增大,动叶的切割作用增强,尾迹涡脱落的频率增加,引起边界层的强烈扰动,造成叶栅通道中熵值逐渐增大,导致较大的能量损失.

(3)当尾迹涡发生脱落时,由于动叶吸力面强逆压梯度的作用,在吸力面前缘发生分离,并在对侧压力面的剪切层中形成高压区,使压力面剪切层形成集中涡,导致压力面的熵值大于吸力面.

[1] SINHA A K,BOGARD D G,CRAWFORD M E.Film cooling effectiveness dow nstream of a single row of holes w ith variab le density ratio[J].Journal of Turbomachinery,1991,113(3):442-450.

[2] MEHENDALE A B,HAN J C,OU S,et al.Unsteady w ake over a linear turbine b lade cascade w ith air and CO2film injection:part2—effect on film effectiveness and heat transfer distributions[J].Journal of Turbomachinery,1994,116(4):730-737.

[3] WALKER G J.The turbulent boundary layer on an axial comp ressor b lade[R].United States:ASM E Paper,1982.

[4] PFEIL H,HERBST R,SCHRODER T.Investigation of the lam inar-turbulent transition o f boundary layers disturbed by w akes[J].Journal of Engineering for Power,1983,105:130-137.

[5] SONDAK D L,DORNEY D J.Vortex shedding in a turbine cascade[J].International Journal of Turbo and Jet Engines,1999,16(2):577-593.

[6] MOCZALA M,LAVANTE E V,PARV IZIN IA M.Numerical investigation of losses due to unsteady effects in axial turbines[J].ASME Paper,2003,388(38):175-198.

[7] 郭婷婷,邹晓辉,刘建红,等.扇形喷孔气膜冷却流场的大涡模拟[J].动力工程,2008,28(2):185-189.GUO Tingting,ZOU Xiaohui,LIU Jianhong,et al.Large eddy simu lation on field of film coo ling w ith a cone-shaped ho le[J].Journal of Power Engineering,2008,28(2):185-189.

[8] 李少华,张玲,张伟宏,等.复合角度气膜冷却叶片的数值模拟[J].动力工程,2009,29(10):919-925.LI Shaohua,ZHANG Ling,ZHANG Weihong,et a l.Numerical simulation on air film cooled b lade with compound angles holes[J].Journal of Power Engineering,2009,29(10):919-925.

[9] 袁锋,吴亚东,竺晓程,等.旋转对涡轮叶片气膜冷却影响的数值模拟[J].动力工程,2007,27(2):161-164.YUAN Feng,WU Yadong,ZHU Xiaocheng,et al.Numerical simu lation study on the effect of rotation on film cooling of turbineb lades[J].Journalo f Power Engineering,2007,27(2):161-164.

[10] RH IE C M.Development and app lication o f amu ltistage Navier-Stokes slover:part I-multisatge modeling using body-faces and determ inistic srtesses&part II-app lication to a high-p ressure comperssor design[J].Joumalof Turbomachinery,1998,120(10):205-223.

[11] 祝昭.转/静交界面处理方法研究及涡轮结构与气动分析[D].南京:南京航空航天大学能源与动力学院,2008.