不同攻角下压气机叶栅涡流噪声辐射特性的研究

柳晓丹, 杨爱玲, 戴 韧, 陈康民

(上海理工大学 能源与动力工程学院,上海 200093)

众所周知,一个好的叶轮机械不仅要具备良好的气动性能而且要有良好的噪声特性.叶栅的气动性能一直是人们设计叶轮机械所关注的重点问题[1],对不同几何参数和气流条件下叶栅气动性能的研究已经相当成熟,如NACA 65系列叶型就有较全面的试验数据库[2].然而,有关叶型参数对噪声性能影响的研究还不是很成熟,且目前的研究大部分是针对单个翼型噪声的[3-4],关于叶栅流场流动噪声源的产生及辐射特性的研究仍然少见公开报道.近年来,叶轮机械的非定常流动越来越受关注,一些学者开展了平面叶栅非定常流场的数值和试验研究,其中包括对叶片尾缘涡脱落特性的研究[5-7],结果表明:叶栅尾缘涡脱落与来流马赫数和攻角有密切关系,随着气流参数的变化,叶栅尾缘涡脱落的频率也发生变化.气动噪声是非定常流动的必然结果,叶栅的尾涡脱落现象对流动噪声的产生和辐射必然有较大影响.探索压气机叶栅涡脱落现象及其与声辐射的关系对于认识叶栅声学性能有很重要的意义.

笔者针对NACA 65系列叶型形成的某低速压气机叶栅,采用非定常流场数值模拟方法得到不同来流攻角下的叶栅流场,研究叶栅尾涡脱落现象以及尾涡强度的变化规律.最后根据非定常流场计算结果,利用边界元方法计算叶栅流场的噪声辐射,研究来流攻角对叶栅噪声辐射特性的影响.

计算声场的流程示于图1,主要包括两部分内容:(1)叶栅非定常湍流流动的数值模拟,通过流场计算可以得到流场结构和声源两方面信息;(2)将叶栅表面的非定常压强作为声源信号,利用边界元方法(BEM)计算该流动声源向外辐射的噪声.

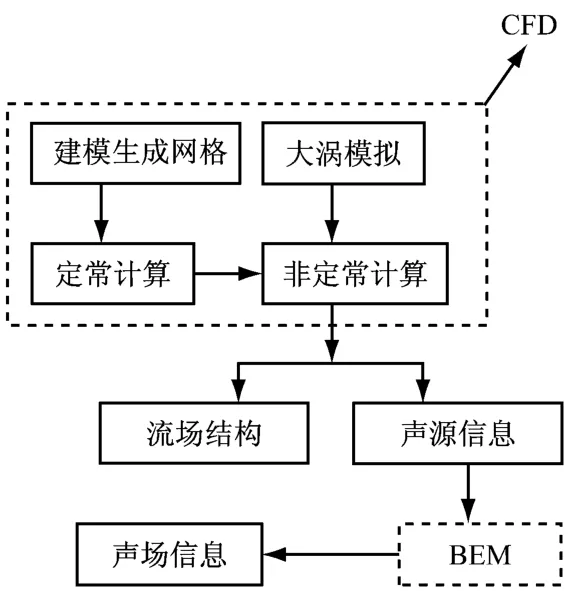
图1 计算流程示意图Fig.1 Schematic flow chart of calculation

1 计算模型和数值模拟方法

表1给出了压气机叶栅的基本参数,参数的定义见图2.其中:t为栅距;b为弦长;w为来流速度;叶型弦线与y轴的夹角γ为安装角;β为来流速度与y轴的夹角,为本文的进气角;α为β与γ之差,即本文的攻角,通过改变来流方向可获得不同的来流攻角.

表1 叶型几何参数和气动参数Tab.1 Geometry and aerodynamic parameters of cascade

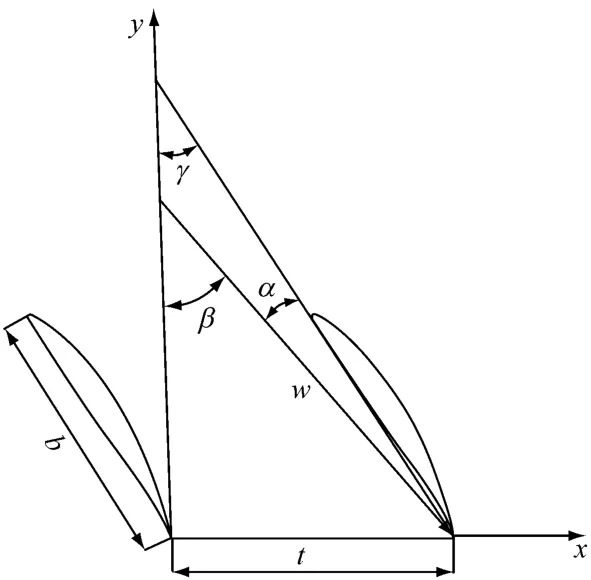
图2 叶栅参数示意图Fig.2 Schematic diagram of various cascade parameters

图3为计算域及计算网格示意图.计算域在流向的总长为6倍弦长,其中栅前1倍弦长,栅后4倍弦长.为了获得高质量的结构化网格,采用Gambit模块对叶栅流道进行多区域网格划分,并且在叶片表面、前缘和尾缘进行网格加密,计算域的总网格数为44 420.利用Fluent商用软件分别对叶栅流动进行了定常和非定常数值模拟.定常流场基于雷诺平均Navier-Stokes方程组和S-A模型,采用速度与压力藕合的Simple算法进行求解,进口边界处给定来流速度的大小和方向,出口则给定压强.非定常流场计算是在定常流场计算结果的基础上进行的.为了较好地捕捉叶栅表面的湍流信息,笔者在非定常流场计算时采用大涡模型进行湍流模拟.根据大涡模拟对网格的要求,叶片表面计算网格的y+值都在1以下.采用Smagorinsky-Lilly亚格子尺度模型,计算时间步长为9×10-6s.

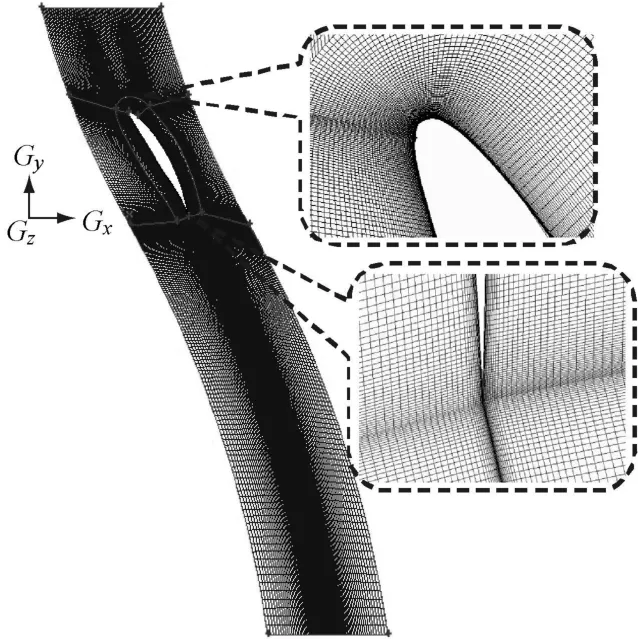
图3 叶栅网格图Fig.3 G rid division of cascade

对于封闭边界外部声场辐射问题,外部声场空间中任意一点声压均满足Helmholtz的边界积分方程[8],即:

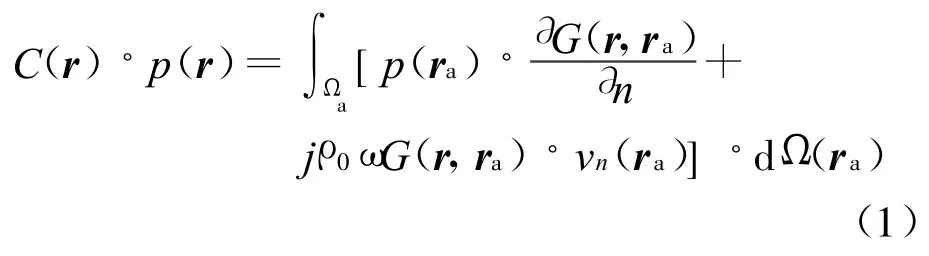
式中:Ωa为在声学空间V中定义的一个声学边界,如图4所示;r表示任意点A(x,y,z)的位置向径;r a则表示声学边界 Ωa上任意点的位置向径;C(r)的值取决于 A点的位置:当 A位于 Ωa内部时,C(r)=0;当A位于Ωa上的非奇异点时,C(r)=1/2;当A位于 Ωa外部时,C(r)=1.

从边界积分方程可知,只需已知边界面表面的p(ra)和v(ra)值,即可由上式积分求解r处的声压值.本文的声场计算通过声学软件LMS中的声学边界元模块实现.首先,将叶栅表面压力脉动作为声源信号导入 LMS中的边界元模块中,并将其进行快速傅里叶变换,将声源时域信号转化为频域信号;然后,定义叶栅表面为声学边界;最后,将变化后的声源频域信号作为声学边界条件,进行外部声场的辐射计算.

图4 外部声场辐射示意图Fig.4 Acoustic radiation of outer field

2 流场计算结果与分析

图5给出了α=16.1时叶片表面的压力系数分布,其中横坐标表示弦长的百分比,纵坐标表示压力

定义压力系数为:系数.由图5可以看出,计算结果与试验值在叶片的压力面较吻合,在吸力面不太吻合,在吸力面弦长40%～60%的地方误差较大.从试验值可以看出,在吸力面弦长40%～60%的地方,压力系数出现了微小的突起,此处出现了分离泡.笔者没有模拟出吸力面的分离泡现象,但是数值计算结果与试验结果整体还是比较接近的,验证了计算的正确性.由于定常计算时采用的湍流模型为一方程湍流模型(S-A模型),可能导致了较大的湍流模拟误差.

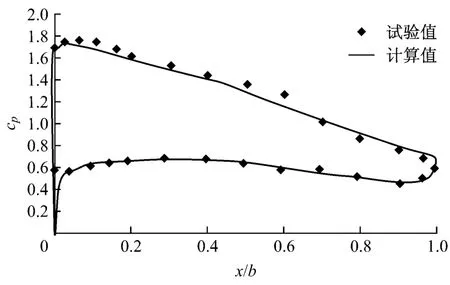
图5 α=16.1时叶片表面的压力系数Fig.5 Surface pressure coefficient of blade atα=16.1

图6给出了不同攻角下的涡量分布(由于篇幅的关系,只给出了几个有代表性的攻角).从图6中可以看出:叶栅的流动表现出尾缘涡脱落现象,不同攻角下涡脱落的结构不同.在5°攻角下,涡脱落表现为类卡门涡街现象,此时流体流动的贴壁性较好,没有发生分离现象,涡成对存在.而在-5°攻角下,压力面产生了分离,压力面产生的分离涡与尾缘涡相互干扰,影响了尾缘涡的脱落结构,使得尾缘涡脱落不再表现为对称涡.在20°攻角下,吸力面产生了大面积的分离,吸力面的分离涡同样与尾缘涡脱落相互干扰,影响了尾缘的涡脱落结构,使得涡脱落充满整个流道.

图7给出了不同攻角下叶栅的升力系数.从图7中可以看出,在5°攻角下,叶栅的升力系数呈现出明显的周期性变化,且变化幅度不是很大,但在-5°和20°攻角的情况下,叶栅升力系数的周期性表现得不是很明显,且变化范围较大,在20°攻角下的变化范围最大.这与图7所示的涡脱落的结构相对应,规则的涡脱落现象造成周期性的压力脉动,不规则的涡脱落现象引起非周期性的压力脉动.由图7还可以看出,大攻角情况下存在吸力面大面积的分离,压力脉动的变化范围比较大,这是由于此时涡脱落的强度较大引起的.在负攻角的情况下,压力面存在分离,此时压力脉动的变化范围也比较大.不同的压力脉动必定产生不同的声场信息,因此将叶片表面的压力脉动作为声源信号进行声场计算.

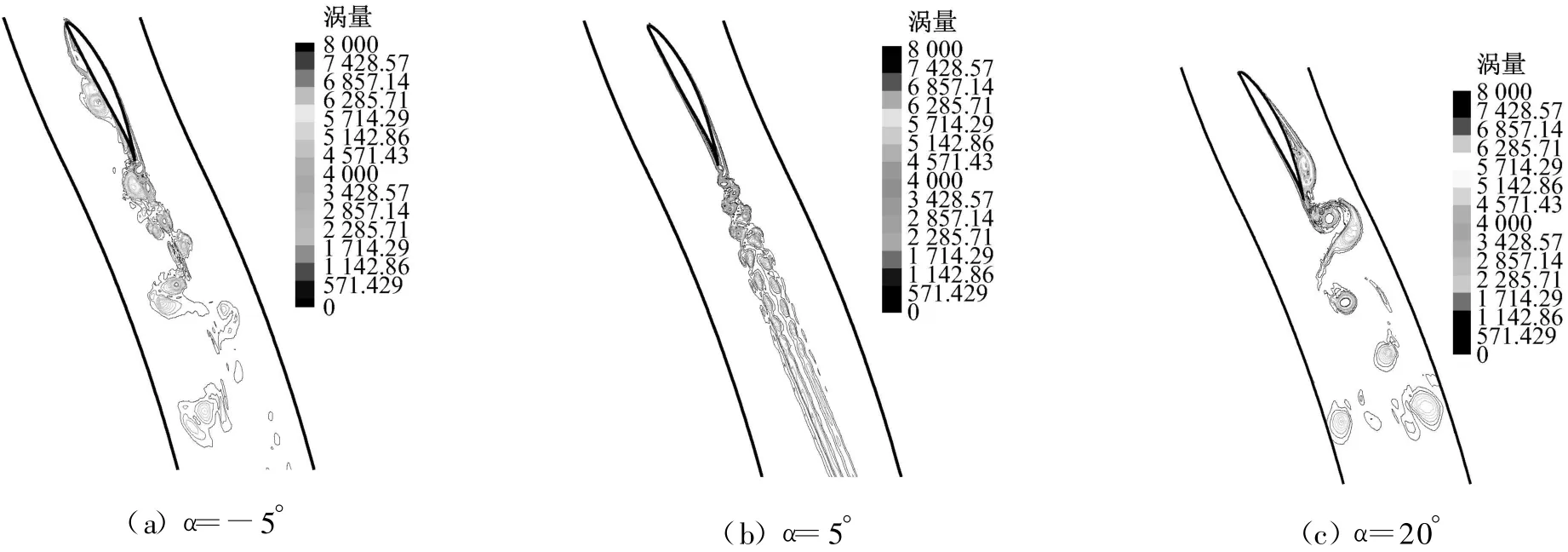
图6 不同攻角下的涡量分布图Fig.6 Vorticity map under different angles of attack

图7 不同攻角下的升力系数曲线图Fig.7 Lift coefficient curve under different angles of attack

3 声学计算结果与分析

通过声学软件LMS中的声学边界元模块来进行声学计算.计算所取的观测点在同一穿过z轴的平面内(xy平面),如图8所示,是一个以坐标原点为圆心、半径 R=0.6 m的圆周,每隔 10°取一个观测点,0°位置表示从圆心到尾缘点连线方向,逆时针方向为正.图9给出了不同攻角下各观测点的噪声分布,该图仅给出了频率 f=222.2 Hz时的声压值.从图9中可以看出:在R=0.6m的圆周上,0°攻角下的叶栅声压级基本上都小于其他攻角下的声压级,随着攻角的增大和减小,叶栅的声压级基本上是增大的,但是在大攻角15°和 20°的情况下,声压级的差别很小;在同一工况下,声压级的最小值出现在叶栅弦线所在的直线方向;攻角的变化并没有改变噪声的指向性分布.

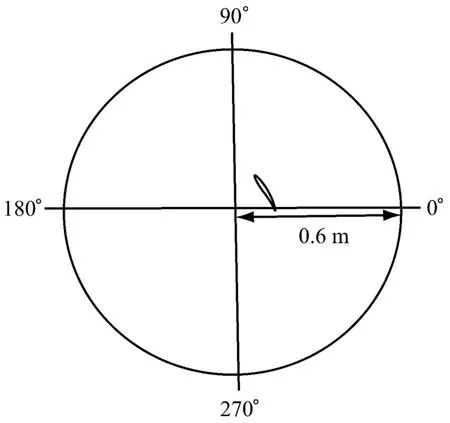
图8 指向性方向示意图Fig.8 Schematic diagram of directional orientation

图9 f=222.2 Hz时噪声指向性分布图Fig.9 Directional distribution of noise at f=222.2 Hz

对45°方向上的观测点(1 000,1 000,0)的声压级进行计算,得到不同频率下的声压级分布(图10).由图10可见,在所有攻角下都存在一个声压级的峰值,且均出现在200 H z左右,随着频率的增大,声压级呈衰减的趋势;在15°和 20°攻角下,声压级的峰值比较大,但并不是所有频率下的值都大于其他攻角下的值.对人耳可听的声压频率范围(20～20 000 Hz)进行叠加,得到总的声压级见图11.由图11可知,在-5°～ 10°攻角范围内,总声压级的变化比较明显,呈现先减小后增大的趋势,在0°攻角下总声压级的值最小.

图10 声压级的频谱图Fig.10 Spectrum of sound pressure level

图11 总声压级曲线图Fig.11 The curve of total sound pressure level

图12给出了不同攻角下的阻力系数曲线.对比阻力系数曲线和声压级曲线图可以发现,不同攻角下声压级曲线的变化趋势与阻力系数曲线的变化趋势较相似,最小声压级出现在阻力系数最小的攻角下.由于涡流噪声是由紊流边界层及其脱离引起气流压力脉动造成的,从流体力学的角度分析,阻力系数最小时,黏性阻力比较小,附面层的厚度比较薄,流动不容易发生分离,此时涡流噪声也比较低.

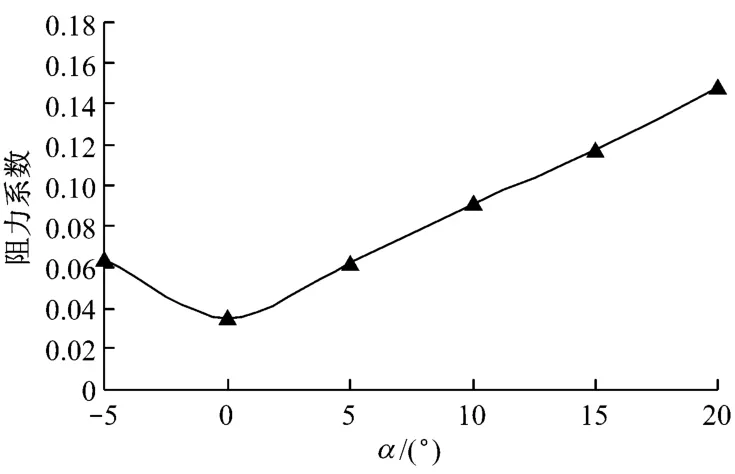
图12 阻力系数曲线Fig.12 The curve of drag coefficient

4 结 论

(1)叶栅流动主要表现为叶片尾缘的涡脱落现象,大正攻角和负攻角下叶片表面的分离影响尾缘涡脱落.

(2)0°攻角下的叶栅声压级最小,随着攻角的增大和减小,叶栅的声压级基本上是增大的.

(3)在同一工况下,声压级的最小值出现在叶栅弦线所在的方向.

(4)叶栅噪声最小值出现在阻力系数最小的攻角下.

[1] 季路成,项林,躲江,等.非定常环境下叶栅性能的数值研究[J].工程热物理学报,2003,24(2):211-215.JI Lucheng,XIANG Lin,DUO Jiang,et a l.Numerical studies about the aerodynamic performance of cascades in unsteady environment[J].Journal of Engineering Therm ophysics,2003,24(2):211-215.

[2] HERRIG L Joseph,EMERY James C,ERW IN John R.Systematic two-dimensional cascades o f test of NACA 65-Series compressor b lades at low speeds[R].Washington:NACA TN 3916,Langley Research Center,1957.

[3] SASAK ISoichi,TAKAM ATSU Hajime,TSUJINO Masao.Influence of separated vortex on aerodynamic noise of an airfoil blade[J].Journal of Thermal Science,2010,19(1):60-66.

[4] QIAO Weiyang,UIF Michel.Theoretical investigation of vortex shedding noise from the wake of air foil[J].Chinese Journal of Aeronautics,2001,14(2):65-72.

[5] 张华良,董学智,谭青春,等.扩压叶栅二维流动分离的数值模拟[J].工程热物理学报,2008,29(8):1297-1300.ZHANG Hualiang,DONG Xuezhi,TAN Qingchun,et al.A numerical investigation of flow separations in a two-dimensional compressor cascsde[J].Journal of Engineering Thermophysics,2008,29(8):1297-1300.

[6] 张文龙,袁巍,张健,等.压气机二维叶栅涡脱落的数值模拟[J].航空动力学报,2002,17(5):556-560.ZHANG Wenlong,YUAN Wei,ZHANG Jian,etal.Numerical simulation o f trailing edge vortex shedding in a 2-D compressor cascade[J].Journal of Aerospace Power,2002,17(5):556-560.

[7] CURRIE T C,CARSCALLEN W E.Simulation of trailing edge vortex shedding in a transonic turbine cascade[J].Journal of Turbomachinery,1998,120(1):10-19.

[8] 王元淳.边界元法基础[M].上海:上海交通大学出版社,1987.