浮力对湍流旋流火焰影响的数值模拟

庞 杰, 张 健

(清华大学 工程力学系,北京 100084)

许多条件下燃烧火焰具有较低的流向速度或Froude数(Fr=u2/g l),如各种层流火焰、火灾中可燃物表面附近的湍流火焰、旋风炉和四角切圆锅炉炉膛中的湍流火焰等.在这类火焰中,气体流动和燃烧过程以及火焰结构与输运特性等都会受到浮力的作用.对这类火焰的理论描述和数值模拟需要考虑浮力的影响.

已有学者对受浮力作用的湍流火焰进行了理论与数值模拟研究.Jeng等[1]采用k-ε-g模型对静止空气环境中受浮力作用的甲烷湍流扩散火焰进行了数值模拟,得到的气体温度场和组分体积分数场基本与试验数据相符.Liu等[2]分别应用代数Reynolds应力/热流通量模型和低Re数k-ε模型对受浮力作用的天然气湍流扩散火焰进行了数值模拟,前者得到的气体速度场和温度场与试验数据相符.Xin等[3]采用快速反应的混合物分数湍流燃烧模型对静止空气中受浮力作用的甲烷湍流火焰进行了大涡模拟,得到的气体速度、温度和混合物分数分布基本与试验数据相符.

旋流燃烧在各种工程燃烧反应装置(如四角切圆锅炉和旋风炉)中有许多应用[4].然而,在现有对受浮力作用的湍流火焰的数值模拟研究中,较少涉及浮力对湍流旋流火焰的影响.为合理地描述并预测湍流旋流火焰的特性,笔者对低Fr条件下的湍流旋流火焰进行了数值模拟,研究了浮力对具有不同初始切向动量或旋流数的湍流旋流火焰的影响,并将模拟结果与试验数据进行了对比.

1 数学模型与数值解法

对受浮力作用的湍流旋流燃烧的模拟,已有的湍流模型包括浮力修正的k-ε模型、Reynolds应力输运方程模型和代数Reynolds应力模型等[5],但后两种模型应用尚不多.笔者采用浮力修正的k-ε模型[6]对受浮力作用的湍流旋流火焰中湍流输运进行了模拟,除在气体平均动量方程中引入浮力作用项外,还在湍流参数如湍流动能k及其耗散率ε方程中引入了浮力修正项.

浮力修正的k-ε模型中k方程和ε方程的具体形式分别为:

对湍流燃烧采用涡团耗散(EDC)模型,对气体辐射传热采用四热流通量模型.在轴对称坐标系中建立受浮力作用的湍流旋流火焰的平均控制方程组,略去方程中各一阶矩上的平均号“ˉ”,各控制方程的通用形式可表示为:

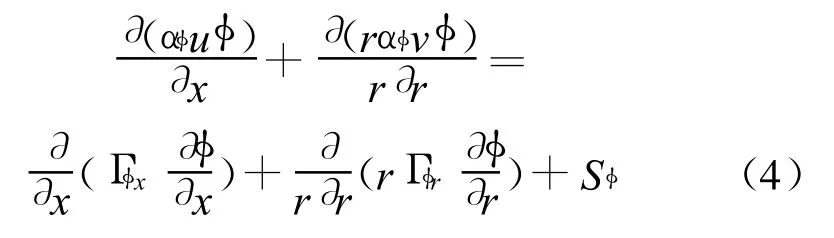
当 αφ=ρ,φ=1、u、v 、w 、k、ε、h 和Y s时 ,式(4)分别对应连续、轴向动量、径向动量、切向动量、湍能、湍能耗散率、焓和组分质量分数方程;当αφ=0,φ=Rx和Ry时,式(4)分别对应轴向与径向辐射热流方程.

为求解上述受浮力作用的湍流旋流火焰平均控制方程组,采用有限容积法[5]对各控制方程进行离散化.在求解区域上布置交错网格系,各控制方程中的对流-扩散项采用混合格式离散,对源项进行负斜率线性化处理,k和ε方程浮力产生项中的密度梯度采用中心格式离散.对各变量离散化方程组的求解采用沿流动方向从上游到下游的逐线 TDMA低松弛迭代算法,对压力与速度的耦合求解采用Simp le算法.

2 计算工况

对旋流燃烧室内受浮力作用的湍流火焰进行了数值模拟.图1所示为圆柱形旋流燃烧室,该燃烧室竖直向上布置.在燃烧室进口处,空气分为旋流一次风和直流二次风,分别通过同轴的内、外环形通道进入燃烧室内,气体燃料则通过同轴的中心管喷入燃烧室.中心燃料管、旋流一次风管、直流二次风管和燃烧室的内直径分别为 8mm、40 mm、58 mm和160mm,外直径分别为 14 mm、44 mm、68 mm 和236 mm,燃烧室长度为1 000 mm.

图1 圆柱形旋流燃烧室示意图Fig.1 Schematic diagram of the cylindrical swirl combustion chamber

数值模拟采用自行编制的湍流多相流动与燃烧计算程序CCVC进行,选取与文献[7]和文献[8]试验条件相同的三组工况.表1给出了三组工况下燃烧室各进口的参数,包括燃料、一次风和二次风进口处的流量和轴向速度,一次风进口处的旋流数和切向速度.燃烧室各进口处的气体温度均按实测的环境温度取为282 K,燃烧室外壁面温度按试验测得的平均值取348 K,燃烧室底壁内侧表面温度也取348 K.从表1可以看到,工况1和工况2的差异仅在于一次风进口处的切向速度和旋流数不同.对比这2组工况的模拟结果可以得出浮力对具有不同旋流数的湍流火焰的影响.

表1 工况参数Tab.1 Parameters for calculation

由于所研究的对象具有轴对称性,仅对燃烧室的半个纵剖面进行计算.计算时沿轴向和径向共选取了62×44个网格节点,且均采用非均匀网格布置.在燃料与空气进口、轴线、壁面及燃烧室出口附近网格布置相对较密.

3 结果与讨论

图2～图6给出了三组工况下受浮力作用的湍流旋流火焰的模拟结果.为对比浮力的影响,图中还同时给出了平均动量方程中不含重力项,且采用不含浮力修正的k-ε湍流模型的模拟结果.将工况1和工况2的气体温度及O2和CO2体积分数分布的计算结果与文献[7]的试验数据进行了比较,将工况3的气体轴向速度和轴向脉动速度均方根值分布计算结果与文献[8]的试验数据进行了对比.

图2(a)给出了工况1下气体温度分布的模拟结果,并与文献[7]的试验数据进行了对比.在燃烧室前部,浮力修正的k-ε模型与k-ε模型的计算结果差异较大.在靠近壁面的区域内,采用浮力修正的k-ε模型预测得到的温度与试验数据相符,而采用k-ε模型计算出的温度则高于试验值.在中心区域,采用浮力修正的k-ε模型比k-ε模型计算得出的温度峰值更靠近轴线,高温区的径向范围更窄,与试验结果更接近.在燃烧室后部,两种模型计算得到的温度分布趋于均匀,且二者逐渐接近,并均与试验结果相符.图2(b)给出了工况1下O2体积分数分布的模拟结果与试验结果的比较.在燃烧室前部,采用浮力修正的k-ε模型计算出的O2体积分数在近壁区域与试验值相符,在轴线附近较试验值偏低,而采用k-ε模型预测得出的O2体积分数比试验值和浮力修正的k-ε模型的计算结果均偏低较多.在燃烧室后部,两种模型的计算结果逐渐趋于一致,均与试验结果相符,O2体积分数分布趋于均匀.

图2 工况1下气体温度和O2体积分数模拟结果与试验数据的比较Fig.2 Comparison between calculated and experim ental results for gas temperature and O2 volume fraction in case 1

图3(a)给出了工况1下CO2体积分数分布的模拟结果,并与文献[7]中的试验数据进行了对比.在燃烧室前部除中心轴线附近以外的区域,采用浮力修正的k-ε模型计算出的CO2体积分数与试验值相符,而采用k-ε模型得到的CO2体积分数则比试验值偏高,只在近壁区与试验值相符.在中心轴线附近的区域,两种模型的计算结果较接近,在燃烧室进口处均比试验值偏低,在远离进口处则与试验值相符.在燃烧室后部,浮力修正的 k-ε模型与k-ε模型的计算结果相差较小,均与试验值相符,CO2体积分数分布趋于均匀.图3(b)给出了工况1下CH4体积分数分布的模拟结果.CH4体积分数在燃烧室中心区域较高,近壁区域较低,峰值位于中心轴线处.采用浮力修正的k-ε模型与k-ε模型计算得到的结果有一定差异,前者预测得到的CH 4体积分数峰值比后者高一些,且体积分数较高区域的范围窄一些.从图3(b)中还可以看出,伴随燃烧的进行,轴线处CH4体积分数峰值沿轴线逐渐下降,到燃烧室后部,燃料已消耗完毕.

图3 工况1下CO2和CH4体积分数模拟结果及其与试验数据的比较Fig.3 Comparison between calculated and experim ental results for CO2 and CH4 volume fraction in case 1

图4(a)给出了工况2下气体温度分布的模拟结果及其与试验数据的比较.在燃烧室前部,气体温度在中心区域较高,近壁区域较低.在近壁区域,采用浮力修正的k-ε模型和k-ε模型计算得到的气体温度分布均与试验结果相符.在中心区域,两种模型计算得到的气体温度均比试验值偏高,且采用浮力修正的k-ε模型计算得到的温度分布与试验结果更接近,高温区范围更窄.在燃烧室后部,两种模型得到的温度分布仍比试验值偏高,但趋势上与试验结果相符,温度分布逐渐趋于均匀,且浮力修正的k-ε模型比k-ε模型的计算结果更接近试验值.图 4(b)给出了工况2下O2体积分数分布模拟结果与试验结果的比较.在燃烧室前部的中心区域,浮力修正的k-ε模型和k-ε模型计算出的O2体积分数均低于试验值,但前者的计算结果与试验值更接近.在燃烧室前部的近壁区域,两种模型的计算结果一致,均与试验数据相符.在燃烧室后部,两种模型预测得出的O2体积分数均比试验值偏低,其中采用浮力修正的k-ε模型计算出的O2体积分数分布较平缓,趋势上与试验值更接近.燃烧室内O2体积分数分布的特点是中心区域较低,壁面附近较高,在燃烧室后部趋于均匀.

图4 工况2下气体温度和O2体积分数模拟结果与试验数据的比较Fig.4 Comparison between calculated and experimental results for gas temperature and O2 volume fraction in case 2

图5(a)给出了工况2下CO2体积分数模拟结果及其与试验数据的比较.在燃烧室前部靠近壁面的较大区域及中心轴线附近,采用浮力修正的k-ε模型和k-ε模型计算出的CO2体积分数分布很接近,在近壁区域与试验数据相符,在中心轴线附近则比试验值偏低.在偏离轴线的区域,两种模型计算得到的CO2体积分数均比试验值偏高,其中浮力修正的k-ε模型的计算结果与试验值更接近,CO2体积分数较高的区域也略窄一些.在燃烧室后部,CO2体积分数分布趋于均匀,两种模型预测得到的CO2体积分数均与试验值相符.图5(b)给出了工况2下CH4体积分数分布的模拟结果.采用浮力修正的k-ε模型与k-ε模型预测得出的CH4体积分数的分布趋势一致.由于燃料的消耗,CH4体积分数沿轴向和径向均较快地降低到接近零,体积分数峰值位于中心轴线上.采用浮力修正的 k-ε模型计算出的CH4体积分数比k-ε模型的结果低一些,燃料沿径向的消耗要快一些.

图5 工况2下CO2和CH4体积分数模拟结果及其与试验数据的比较Fig.5 Comparison between calculated and experimental results for CO2 and CH4 volume fraction in case 2

图6(a)给出了工况3下气体轴向速度分布的模拟结果,并与文献[8]的试验数据进行了比较.在靠近壁面的区域,浮力修正的k-ε模型和k-ε模型的计算结果较接近,均与试验值相符,其中前者与试验值符合得更好.在燃烧室中心区域,浮力修正的k-ε模型比k-ε模型预测得出的轴向速度偏高,而后者与试验值更接近.图6(b)给出了工况3下气体轴向脉动速度均方根值分布的模拟结果,并与试验数据进行了对比.在靠近燃烧室进口的2个截面上,浮力修正的k-ε模型和k-ε模型的计算结果相差不大,均与试验值相符.在x/R=1.81的截面上,浮力修正的k-ε模型预测得出的轴向脉动速度均方根值比k-ε模型预测得出的大,且与试验值更接近.而在中心轴线处,k-ε模型的预测结果与试验值更接近.

4 结 论

(1)采用浮力修正的k-ε模型计算得到的不同工况下的O2和CO2体积分数分布均与试验结果相符,得到的气体温度、轴向速度和轴向脉动速度均方根值分布基本与试验结果相符.

(2)采用浮力修正的k-ε模型计算得到的气体组分体积分数场、温度场和轴向脉动速度均方根值分布比k-ε模型的计算结果有较明显的改进.在燃烧室前部,各物理量变化较剧烈,浮力修正的k-ε模型和k-ε模型的计算结果差别较大.在燃烧室后部,各物理量变化趋于平缓,浮力修正的k-ε模型与k-ε模型的模拟结果相差不大.

(3)采用浮力修正的k-ε模型计算得到的气体温度峰值更靠近轴线,高温区的径向范围更窄,气体组分体积分数变化较大的区域也更窄且更集中在轴线附近.

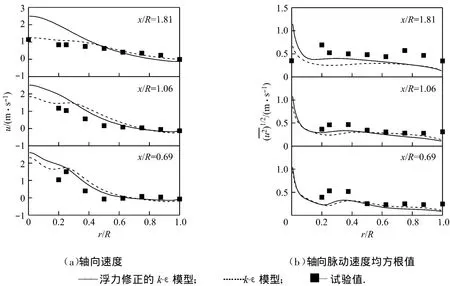
图6 工况3下气体轴向速度和轴向脉动速度均方根值模拟结果与试验数据的比较Fig.6 Comparison between calculated and experimental results for gasaxial velocity and root mean square of axial fluctuating velocity in case 3

(4)在燃料和空气的初始轴向动量相同的条件下,对于初始切向速度或旋流数相对较高的湍流火焰,采用浮力修正的k-ε模型与k-ε模型得到的模拟结果差异更明显,说明浮力对切向速度或旋流数较高的湍流火焰影响更大.

[1] JENG SM,FAETH G M.Species concentrations and turbulence properties in buoyant methane diffusion flames[J].ASME JHeat Transfer,1984,106(4):721-727.

[2] LIU F,W EN JX.The effect of turbulence modeling on the CFD simulation of buoyant diffusion flames[J].Fire Safety Journal,2002,37(2):125-150.

[3] XIN Y,GORE JP,MCGRATTAN K B,et al.Fire dynamics simulation o f a turbulent buoyant flame using a mixture-fraction-based combustion model[J].Combustion and Flame,2005,141(4):329-335.

[4] 杨震,庄恩如,张建文,等.大型电站锅炉采用切向燃烧方式燃用无烟煤的研究[J].动力工程,2006,26(6):766-772.YANG Zhen,ZHUANG Enru,ZHANG Jianwen,et a l.Research on tangential firing of anthracite in large capacity station boilers[J].Journal of Power Engineering,2006,26(6):766-772.

[5] 陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2001.

[6] RODIW.环境问题的紊流模型[M].贺益英,译.北京:水利电力出版社,1987.

[7] 普勇,张健,周力行.一次风旋流数对燃烧室内湍流燃烧与NOx生成的影响[J].工程热物理学报,2005,26(增刊):265-268.PU Yong,ZHANG Jian,ZHOU Lixing.Effects of swirl number for the primary air on the turbulent combustion and NOxformation in a swirl combustor[J].Journal of Engineering Thermophysics,2005,26(s):265-268.

[8] 普勇,张健,周力行.旋流燃烧室内湍流燃烧速度场的实验研究[J].力学学报,2003,35(3):341-347.PU Yong,ZHANG Jian,ZHOU Lixing.Measurements of the velocity fields for turbulent combustion in a swirl combustor[J].Acta Mechanica Sinica,2003,35(3):341-347.