基于多模型的循环流化床锅炉床温预测控制
2011-04-13董湛波向文国
董湛波, 向文国, 王 新
(东南大学 能源与环境学院,南京 210096)
循环流化床(CFB)锅炉由于其污染排放低、燃料适应性广、燃烧效率高、负荷适应能力强[1]而受到国内外火力发电厂的青睐,并且日趋往大型化方向发展.但是,CFB锅炉的燃烧系统是典型的多输入/多输出、强耦合、大滞后和非线性系统,常规的控制方法很难取得理想的调节效果[2-3].
针对CFB锅炉燃烧系统各对象间的耦合性,一般将其分解为几个相对独立的调节系统,主要有主蒸汽压力控制系统、床温控制系统、送风控制系统和炉膛负压控制系统等[4].CFB锅炉具有良好的负荷适应能力,常用来担任电网和热网的调峰任务[3],因此负荷在大范围内变动是不可避免的,由此而引起的非线性系统的控制问题也就不可回避了.
在CFB锅炉燃烧系统中,床温是一个非常重要的运行参数,它直接影响到燃烧效率、脱硫效率和机组的经济、安全运行[2-3].因此,研究CFB锅炉床温的动态特性和控制规律对锅炉的实际运行有着重要的意义.本文正是针对负荷大范围变动时床温的调节,以某电厂440 t/h CFB锅炉为例,提出了一种改进的多模型预测控制,并通过仿真验证了其有效性.
1 CFB锅炉床温的动态特性
CFB锅炉的床温在运行中受许多因素的影响,如给煤量、一次风量、二次风量、石灰石量、排渣量和返料量等,其中石灰石量对床温的影响较小,而二次风量主要是确保后期的稳定燃烧.所以,目前国内的CFB锅炉在运行中主要是通过给煤量和一次风量来进行床温调节,床温的设定值则由负荷通过函数发生器自动设定.
文献[4]提供了某电厂440 t/h CFB锅炉床温的传递函数模型.
给煤量-床温的传递函数模型:

式中:K a为静态增益;T a1、T a2为时间常数;τ为纯滞后时间.
K a、T a1、T a2、τ、α都是随运行工况不同而变化的参数.当锅炉负荷在30%~100%额定负荷之间变化时,K a取2~16,T a1、T a2取90~ 120 s,τ取45~180 s,α取 2~16 s.
一次风量-床温的传递函数模型:

式中:K b为静态增益;T b1、T b2为时间常数.
K b、T b1、T b2、β也都是随运行工况不同而变化的参数.当锅炉负荷在30%~100%额定负荷之间变化时,K b取 0.2~1.8,T b1、T b2取 90~ 180 s,β取2~8 s.
根据式(1)和式(2)的模型结构,针对该机组的现场试验数据,采用最小二乘法辨识,并经过优化拟合得到4个典型工况点近似的传递函数模型,模型参数示于表1.

表1 CFB锅炉床温4个典型工况点的模型参数Tab.1 Model parameters for bed temperature of CFB boiler at four different operating points
由于给煤量对床温的影响比一次风量对床温的影响大得多,所以给煤量-床温通道的静态增益要比一次风量-床温通道的静态增益大得多,但是给煤量-床温通道的纯延迟要远大于一次风量-床温通道.随着负荷的变化,给煤量和一次风量都会使床温的动态特性发生明显的变化,但是这个变化是单调的.低负荷时,给煤量阶跃增加,床温的静态增益较大,动态响应时间和纯延迟较长;而一次风量阶跃增加,床温的静态增益较大,但动态响应时间较短.高负荷时则相反[5].
2 广义预测控制(GPC)算法
GPC对大滞后对象的控制效果明显优于PID,由于大量的教材和文献都已经介绍了GPC的算法,所以本文只做简要介绍,具体的推导过程可以参考文献[6].GPC和其他预测控制一样具有三个特点,即预测模型、滚动优化和反馈校正.
GPC用受控自回归积分滑动平均(CARIMA)模型描述受到随机干扰的对象:

式中:A(q-1)、B(q-1)、C(q-1)都是 q-1的多项式;Δ为差分算子;ξ(t)是一个不相关的随机序列;B(q-1)的前若干项可以是零,表示响应的纯滞后步数,通常假设C(q-1)=1.
定义性能指标:
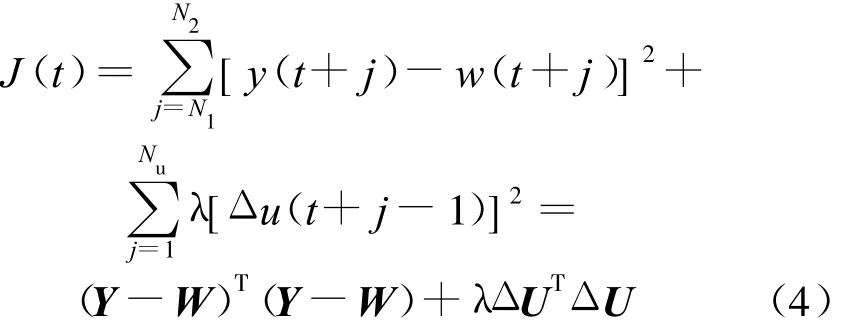
引入一组丢潘图方程:

通过求解丢潘图方程可以得到:

式中:G、H、F 是关于q-1的多项式.令可以得到最优控制规律式

取 ΔU的第一行 Δu(t)=[1,0,…,0]1×ΝuΔU 作为当前时刻的控制增量.
GPC是从自校正控制器发展而来的,保持了自校正的方法原理,在控制过程中不断通过实际输入输出在线估计模型参数,并以此修正控制规律.
将式(3)改写成如下形式:

式中:
(2)当AFA 1和AFA 2的掺量分别为2.5‰和3.0‰时,UHPC的28 d抗压强度分别提高28.5%和21.5%;当AFA 1和AFA 2的掺量分别为3.5‰和3.0‰时,UHPC的28 d抗折强度分别提高了30.2%和28.8%。

采用渐消记忆的递推最小二乘法估计参数向量:

式中:0<μ<1为遗忘因子,常选为0.95~1;K(t)为权因子;P(t)为正定的协方差阵,初始置为P(0)=α2I;α为一足够大的常数.
3 多模型广义预测控制
3.1 上述算法的缺陷
与动态矩阵控制(DMC)相比,GPC在反馈校正环节与之有明显差异.DMC用的是一个不变的预测模型附加一个误差预测模型,这样控制规律式可以离线计算.而GPC是由自校正控制器发展而来的,通过实际输入输出在线估计模型参数,每个采样周期都要求解丢潘图方程并重新计算控制规律式(8),因此在线计算量较大.
GPC是基于模型的控制,而CFB锅炉负荷大范围变动会导致其动态特性发生变化,此时GPC的控制效果就会变差[7].因为如果采用前面所述的递推最小二乘的辨识方法来在线校正预测模型,在实际运行中是有一定缺陷的.首先,这种基于最小二乘的辨识方法采用的是固定结构(阶次和延时)的模型,但是当被控对象的非线性较强时,用同一结构的模型往往很难对整个运行工况进行准确描述,如果再加入模型结构的辨识,则又会加大在线计算量.其次,当存在随机噪声时,用递推最小二乘法估计出的模型参数只能有偏收敛于实际值.第三,当原来的模型失配较严重时,往往模型参数收敛较慢,校正时间较长.所以,通过递推最小二乘法辨识出的模型不能很好地跟踪对象的动态特性,模型往往会发生较严重的失配,导致GPC不能对强非线性对象取得理想的控制效果.
3.2 基于多模型的控制策略
多模型控制的基本思路是采用多个典型工况点模型逼近被控对象整个运行区间的特性,针对每个子模型设计相应的控制器.选取用来表征工况范围的变量,在实际运行中,通过切换或者加权的方式,将这些有限个子控制器输出映射为最终的控制作用[8-9].因此从理论上说,只要在对象模型的变化范围内建立足够多的模型,则实际对象总会与其中一个或几个相同或相似[10].多模型控制中的模型不一定都是固定的模型,也可以是自适应模型,文献[11]和[12]对各种多模型控制策略进行了详细的阐述.
3.3 多模型广义预测控制
当实际对象的动态特性与模型吻合或者较接近时,GPC的在线辨识环节对预测模型不做或只做很小的校正,此时如果取消在线辨识环节,对调节效果几乎是没有影响的,而控制规律式却可以通过离线计算求得.当实际对象的动态特性与固定工况点的模型存在明显偏差时,可以通过多个固定模型逼近的方法来跟踪对象动态特性,从而取代在线辨识,此时各个固定模型对应的控制规律式仍然可以通过离线计算求得.这样既可以迅速跟踪对象动态特性的变化,又减少了在线计算量.
对于多个子控制器,采用线性插值的方法来确定各自的权重,具体算法为:由于模型的参数是随负荷单调变化的,所以选择负荷σ作为表征工况范围的变量,由小到大确定 N 个固定工况 σ1,σ2,…,σn的模型并设计相应的控制器.t时刻,若 σi<σ≤σi+1,则除i和i+1外的其他控制器权值置0,i和i+1控制器权重为最终的控制增量为:
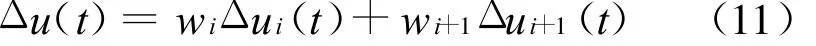
控制器结构图(以4个子控制器为例)见图1.

图1 多模型GPC结构图Fig.1 GPC b lock diagram based on multi-models
4 控制过程仿真
4.1 控制器参数整定
本文采用3.2节中所述的将多模型控制和GPC结合的方法,从克服对象非线性和减少在线计算量的角度,针对CFB锅炉床温的控制进行仿真,仿真是通过Matlab语言编程实现的.
在GPC的参数整定中需要注意的是N1必须大于装置的时滞数[6].控制权系数λ对闭环特性起重要作用,减小λ可以加快调节速度,但会降低稳定性;增大λ则相反[13].当将多个子控制器组合成多模型控制器时,控制器参数需要做相应的修正,采样周期 T、优化时域 N1、N2及控制时域 Nu取相同的值[12].同时,为了减小调节后期的振荡,这里将GPC的性能指标(式(4))修改为:
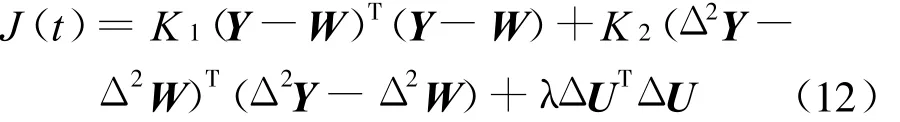

式中:


增大K 1,可以加快调节速度,但也会加剧振荡;增大K 2,可以减轻振荡,但调节速度会变慢[14].这样的修改虽然增加了2个待整定的参数,但是也使得参数整定更具有针对性,就像PID控制器中的3个参数在控制中起着不同的作用,但又相互协调,以确保全过程调节效果良好.为了减小后期的振荡,可以将每一个子控制器的K2适当取大.修正后的多模型GPC和原来的多模型GPC调节效果见图2.原来未使用性能指标式(12),所以调节过程的后期有小幅振荡.修正后由于K 2取值较大,虽然前期的调节速度略慢,但消除了后期的振荡.
采用上述改进的多模型GPC,根据表1的模型参数,对控制器参数进行整定,整定结果分别见表2和表3.

图2 修正前后调节效果的对比Fig.2 Comparison of regulation effect before and after modification

表2 给煤量-床温通道的多模型GPC参数整定结果Tab.2 Parameter setting of the multi-mode-based GPC in coal feeding rate-bed temperature mode
4.2 仿真验证
当温度设定值发生阶跃变化时,用给煤量和一次风量调节床温的响应曲线分别见图3(a)和(b).图中的单模型GPC是按100%额定负荷时的模型设计的,并使用递推最小二乘法在线估计模型参数,而此时锅炉在60%额定负荷附近运行.从图中可以看出,无论是给煤量–床温通道,还是一次风量–床温通道,在模型失配时,多模型GPC的调节速度更快,稳定性也更好.

表3 一次风量-床温通道的多模型GPC参数整定结果Tab.3 Parameter settings of the multi-mode-based GPC in primary air flow rate-bed temperature mode

图3 床温设定值阶跃响应Fig.3 Step response to setpoint of bed temperature
由于CFB锅炉机组常用于调峰,所以负荷短时间内发生大范围变动时有发生.为了维持CFB锅炉的正常运行,床温也必须迅速作出相应的变化.床温对一次风量响应速度较快,但一次风除了调节床温外,还要维持床内颗粒的流化质量,在短时间内不宜频繁变动[4],而且一次风量对床温最终的影响比给煤量的影响小得多.所以通常要对一次风量变化的幅度和速率加以约束,以确保床内拥有稳定的燃烧环境和良好的流化质量.当负荷指令短时间内大范围变动时,主要依靠给煤量来调节床温以维持负荷.该电厂440 t/h CFB锅炉部分工况点稳定运行时的数据见表4,图4为负荷从90%降到55%时床温调节过程曲线,负荷是在265min时发生变化的,其中单模型GPC同图3.从图 4可以看到,与单模型GPC相比,多模型GPC调节过程时间缩短近 10 min,最大动态偏差小了4 K.因为将各个子控制输出增量加权求和,实际上相当于采用较平滑的方法将各个子模型按照其可信度(即权重)组合成与实际对象接近或吻合的模型,不同负荷下被控对象的动态特性都较好地跟踪.

表4 部分工况点稳定运行时的数据Tab.4 Data obtained when the unit working stably at several points

图4 机组负荷大范围变动时的床温调节Fig.4 Bed temperature regulation under great variations of load
5 结 论
(1)将CFB锅炉运行区间分成3个子区间,选择负荷作为表征工况范围的变量,利用离线辨识得到的4个典型工况点的床温模型逼近整个运行区间,从而取代在线辨识来校正模型,使得GPC的控制规律式可以像DMC那样离线计算,减小了在线计算量.
(2)通过对GPC的性能指标进行适当修改,消除了调节后期的振荡.采用线性插值方法确定各子控制器的权值,利用加权求和的方法将各子控制器输出映射为最终的控制作用,算法简单,易于实现.
(3)仿真结果表明,在模型失配或者负荷大范围变动时,本文提出的多模型GPC对被控对象动态特性有良好跟踪能力,控制效果明显优于单模型GPC.
[1] HADAVANDA,JALALI A A,FAMOURIP.An innovative bed temperature-oriented modeling and robust control of a circulating fluidized bed combustor[J].Chemical Engineering Journal,2008,140(1/2/3):497-508.
[2] 赵伟杰,张文震,冯晓露.循环流化床锅炉床温的控制特性[J].动力工程,2007,27(4):545-610.ZHAO Weijie,ZHANG Wenzhen,FENG Xiaolu.Bed temperature control characteristics of CFB boilers[J].Journal of Power Engineering,2007,27(4):545-610.
[3] 牛培峰,张君.循环流化床锅炉燃烧系统聚类融合控制研究[J].中国电机工程学报,2007,27(11):33-39.NIU Peifeng,ZHANG Jun.Research on clustering fusion control for circulating fluidized bed boilers combution system[J].Proceedings of the CSEE,2007,27(11):33-39.
[4] 石岩.循环流化床动态特性及控制规律研究[D].南京:东南大学能源与环境学院,2009.
[5] 仇韬,丁艳军,孔亮,等.CFB锅炉动态特性与负荷和煤质的关系研究[J].中国电机工程学报,2007,27(32):46-51.QIU Tao,DING Yanjun,KONG Liang,et a l.Research of relationship between CFBB dynamic behavior and power and coal quality[J].Proceedings of the CSEE,2007,27(32):46-51.
[6] 钱积新.预测控制[M].北京:化学工业出版社,2007:49-73.
[7] ZHANG Tiejun,FENG Gang,LU Jianhong,et al.Robust constrained fuzzy affine model predictive control with application to a fluidized bed combusion plant[J].IEEE Transaction on Control System Technology,2008,16(5):1047-1056.
[8] 程启明,郑勇.球磨机多模型PID型神经元网络控制系统[J].中国电机工程学报,2008,28(2):103-109.CHEN Qiming,ZHENG Yong.Control system of multi-model PID neuron network for ball mill[J].Proceedings of the CSEE,2008,28(2):103-109.
[9] 杨锡运,徐大平,柳亦兵,等.过热汽温多模型预测函数控制策略的研究[J].动力工程,2005,25(4):536-540.YANG Xiyun,XU Daping,LIU Yibing,et al.Study on strategy of superheated steam temperature control using multi-model predictive functions[J].Journal of Power Engineering,2005,25(4):536-540.
[10] 仇韬,丁艳军,吴占松,等.基于预测模型的多PID控制器模糊加权控制[J].中国电机工程学报,2006,26(24):121-124.QIU Tao,DING Yanjun,WU Zhansong,et al.A new fuzzy-weighted control used multiple PID controller based on prediction mode l[J].Proceedings of the CSEE,2006,26(24):121-124.
[11] 郭启刚.热工过程多模型控制理论与方法的研究[D].保定:华北电力大学能源动力与机械工程学院,2007.
[12] DOUGHERTY D,COOPER D.A pratical multiple model adaptive strategy for single-loop MPC[J].Control Engineering Practice,2003,11(2):141-159.
[13] NESH ASTERIZ A R,SEDIGH A K,SADJADIAN H.Generalized predictive control and tunning of industrial processes with second order plus dead time models[J].Journal of Process Control,2010,20(1):65-72.
[14] 郭伟,王伟.PID型广义预测控制在过热温控中的应用[J].计算机工程,2007,35(11):251-253.GUO Wei,WANG Wei.Application of PID-type generalized predictive control in superheated temperature control system[J].Computer Engineering,2007,35(11):251-253.
