基于微粒群辨识算法的电力负荷综合模型的建模与仿真

谷鹏，石国萍

（1.山东电力建设第一工程公司，山东济南250100；2.山东建筑大学信息与电气工程学院，山东济南250101）

目前电力系统数字仿真已经成为电力系统设计、规划、运行分析的主要手段，其分析结果是制定相应决策的依据和基础。而数字仿真中模型的准确与否将直接影响系统稳定计算结果的精度以及以此为基础的电网决策方案。在现阶段发电机模型和电网络模型已相当成熟的情况下，负荷模型显得相对过于简单，而由于负荷本身的随机性、分散性、多样性和时变性，使得负荷模型的建立十分困难[1]。

电力系统本质上是非线性的高阶复杂系统，通常用降阶的模型系统来动态拟合原系统。非线性系统的参数辨识方法目前大多以优化为基础。在负荷参数辨识中目标函数不可能写出其解析关系，其解空间相当复杂，有多个极值点，且有些极值点之间差异细微。因此,优化搜索方法相当重要。常用的优化搜索方法有最小二乘法、卡尔曼滤波法、爬山类方法、随机类方法等。前2种方法适用于线性系统，爬山类方法基于梯度，因而只能收敛到起始点附近的局部最优点，多峰问题难以搜索到全局最优点,在峡谷则会出现振荡，且要求存在一阶导数甚至二阶导数,故很少用于电力系统参数辨识。微粒群优化(PSO)算法是由James Kennedy和R.C.Eberhart提出的，本质上也属于随机类方法,具有并行处理特征，鲁棒性好，易于实现，原理上可以以较大的概率找到优化问题的全局最优解，且计算效率比传统的随机类方法要高得多[2]。本文将其应用到电力负荷动态参数辨识并收到了良好效果。

1 综合负荷模型

综合负荷模型结构采用三阶感应电动机并联负荷静特性的模型结构[3]。静态特性负荷模型的结构采用扩展ZIP模型或者幂函数模型。扩展ZIP模型部分可以表示为：

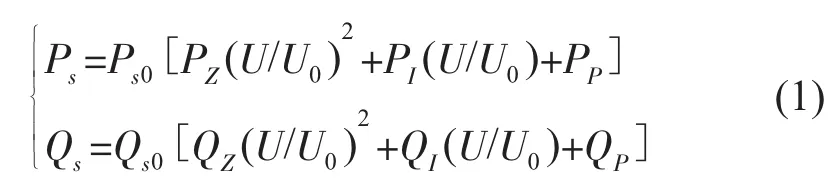
式中：Ps，Qs，Ps0，Qs0为静态负荷部分所消耗的有功功率与无功功率及其初始稳态值；PZ，PI，PP为有功电压特性参数；QZ，QI，QP为无功电压特性参数，系数满足PZ+PI+PP=1，QZ+QI+QP=1；U，U0为母线电压及其初始稳态值。

该综合负荷模型结构中定义了2个参数Kpm与Mlf,使得负荷模型具有了容量自适应特性，实现了模型参数与负荷幅值大小无关的特点。

Kpm用来表示等值电动机在综合负荷中所占的比例，定义为：

式中：P0为负荷测点的初始有功功率；P0'为等值电动机的初始有功功率。

Mlf为额定初始负荷率系数，定义为：

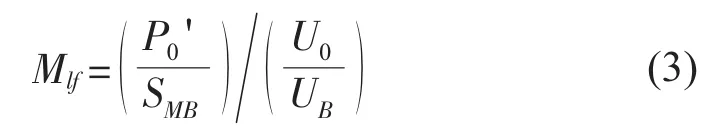
式中：SMB与UB分别为负荷模型中等值电动机的额定容量与额定电压；U0为负荷测点的初始电压。

感应电动机部分采用三阶感应电动机模型，其状态方程和输出方程为:

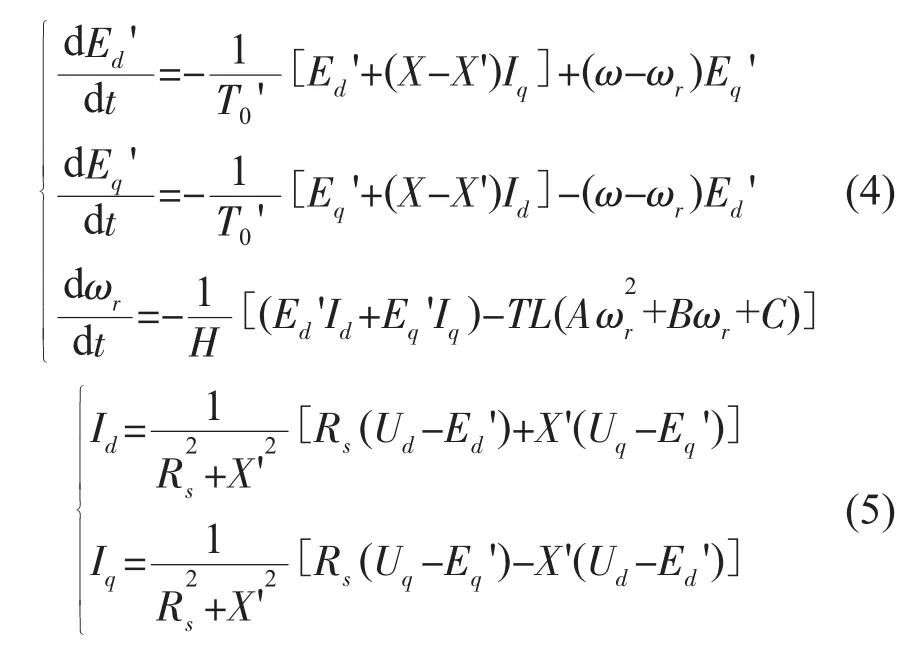
式(4)为感应电动机三阶机电暂态模型状态方程，式(5)为输出方程。式中U是系统的输入，Id，Iq是系统的输出，w为系统运行频率，Rs，Xs为定子绕组的等值电阻和漏抗，Rr，Xr为转子绕组的等值电阻和漏抗，Xm为定子转子互感抗为转速为定子开路暂态时间常数，H为电动机惯性时间常数，Tm=TL为电动机机械转矩为电磁转矩，TL为负载系数，A，B，C为电动机的机械转矩中与转速平方、转速成线性关系及与转速无关部分的比例系数，A+B+C=1。

综合负荷模型待确定的参数有电动机的8个参数：Rs，Xs，Xm，Rr，Xr，H，A，B，加上Kpm，Mlf；对于静态特性部分，如果采用扩展ZIP模型，则有PZ，PI，QZ，QI共4个参数；如果采用幂函数模型，则有PV，QV共2个参数(功率电压特性系数)。

2 参数辨识的PSO算法

以优化为基础的非线性系统的参数辨识方法其主要过程是寻找一组最优的参数向量Z*,使预定的误差目标函数E(Z)值达到最小。在负荷参数辨识中，Z=[pv，qv，Tm，β，M，T'，C，X']，目标函数为有功和无功的误差平方和函数：

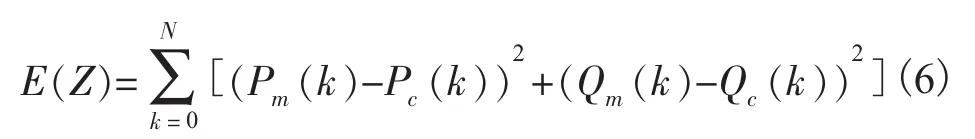
式中：N为测点数；Pm(k)和Qm(k)分别为有功和无功的第k个测量值；Pc(k)和Qc(k)分别为有功和无功的第k个计算值。

E（Z）是很复杂的，可能存在多优化解，所以优化方法必须十分有效。PSO算法是从生物的群体行为规律和社会心理学中得到启发，与其他进化算法不同的是，个体成员在参数定义的多维空间内游走，在个体随机初始化后，将会被随机给定一个增量，在每一代中每个个体(也称为粒子)的增量，是朝着该个体所在的群体的全局最佳位置(具有历来的最大适应度)和它所在的社区最佳位置(即该个体所处的社区中具有最大适应度的个体的位置)的方向前进的。PSO算法从个体行为的评价、比较、模仿三大原则出发，其具体步骤为：（1）在定义域n维空间内随机产生个体群。（2）将它们分为多个社区，社区成员的个数可按需调整，要注意的是社区的划分是网络拓扑意义上的，而不是各个个体在空间的实际位置相近的划在一起，否则会导致容易陷入局部最优。（3）计算每个个体的适应度。取现有群体中具有最大适应度的个体为Pi，取第i个个体所在社区中具有最大适应度的个体为Pg。则第t代第i个个体的迭代增量为：

式中：w，a1，a2均为(0，1)区间上的随机数。

（4）产生下一代个体：

若Xid＞Xid,max，则取Xid=Xid,max；若Xid＜Xid,min，则取Xid=Xid,min。其中，1＜d＜n。

（5）转向执行步骤（2），直到每代最大适应度变化小于给定值，即G(pi(t))-G(pi(t-1))＜ε。

3 算例分析

3.1 故障数据的获取

以EPRI-36节点系统为例，如图1所示。使用PSASP进行仿真，获取负荷建模数据[4-6]。

其中，BUS20采用考虑配电网络的综合负荷模型[5]，电动机参数采用表1中电科院推荐参数，电动机比例Kpm=0.6，负载率Mlf=0.468。静态部分采用4-6模型，配网阻抗ZD=0+j0.061。

表1 典型电动机参数

BUS21采用考虑配电网络的综合负荷模型，电动机参数采用表1中IEEE-6参数，电动机比例Kpm=0.5，负载率Mlf=0.6。静态部分采用3-3-4模型，配网阻抗ZD=0+j0.06。

故障设置如下。

故障1：1s时BUS19-BUS30支路100%处发生三相金属接地故障，1.12s故障切除，系统稳定。

故障2：1s时BUS31-BUS33支路100%处发生三相金属接地故障，1.12s故障切除，系统稳定。

故障3：1s时BUS9-BUS22支路100%处发生单相金属接地故障，1.12s故障切除，系统稳定。

通过PSASP仿真，获取3种故障下母线BUS 20和BUS21的负荷数据，运用粒子群优化算法对该2条母线的负荷模型进行辨识。误差评价指标[7]采用均方百分比误差，避免了均方误差在有功无功数值上相差较大时辨识不合理的缺点：

3.2 综合负荷模型辨识

静态特性部分可以采用扩展ZIP模型或者幂函数模型，幂函数模型对有功功率及无功功率都适用；ZIP模型对于有功功率一般是合适的，但是对于无功功率不一定适合[7]；而其幂函数模型待辨识的参数较少。鉴于此，本文采用幂函数模型。故待辨识参数有Rs，Xs，Xm，Rr，Xr，H，A，B，Kpm，Mlf，PV，QV共12个参数。但若同时辨识这12个参数，一方面会增加计算量，另一方面也会影响辨识精度。本文采用摄动法对参数的灵敏度进行了分析[8，9]，得出灵敏度较大的参数有Xs，Rr，Kpm，Mlf，PV，QV共6个参数。

从表2可以得出这么几点结论：(1)对于同一母线负荷，相同故障形式下的辨识结果基本完全一致；不同故障形式下的辨识结果有一定差异。(2)对于不同母线负荷，在各种故障形式下的参数都存在较大分散性。(3)三相短路故障下的辨识结果比单相故障下的辨识结果更接近真实值。

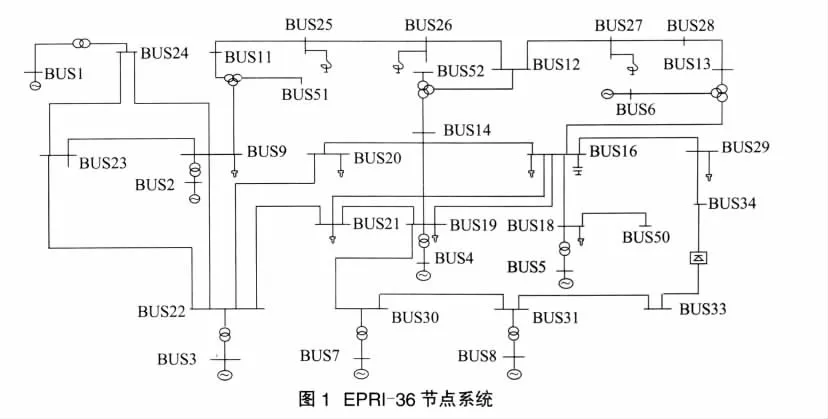
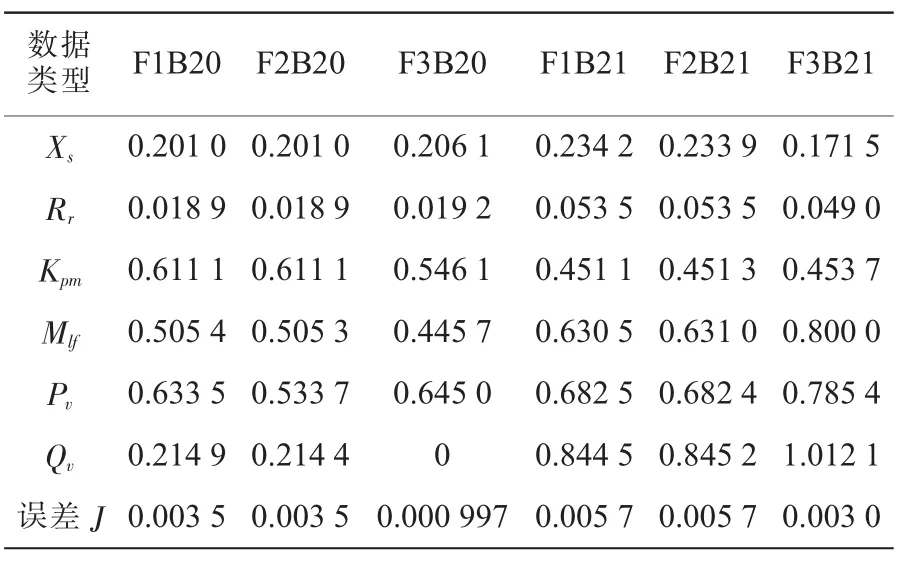
表2 BUS20和BUS21母线负荷在3种故障下的辨识结果

图2为BUS20母线负荷不同故障下的三组辨识结果与实测负荷有功无功的比较。可以看出，虽然同一母线负荷在各种故障形式下的辨识结果存在参数分散性，但是都能对实测有功无功很好的拟合。同样，BUS21母线负荷也得到相同的结论。

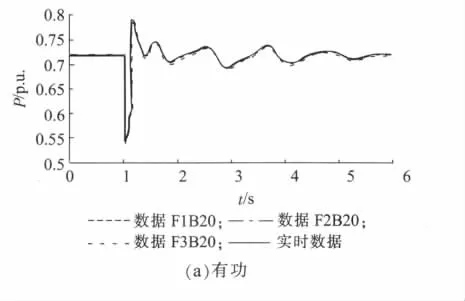
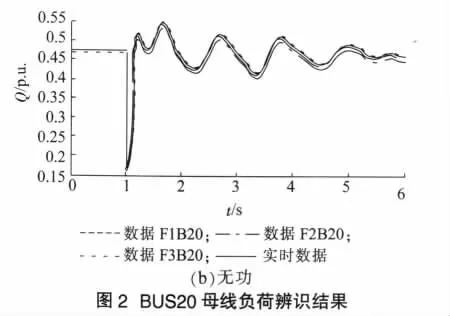
图3为BUS20母线负荷辨识出的3组数据对BUS21母线负荷的拟合。可以看出，尽管这3组数据对BUS20母线负荷的拟合效果很好，但是对BUS21母线负荷的拟合很差。

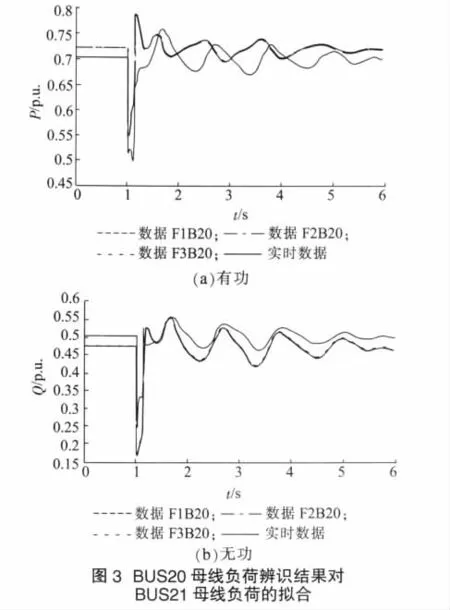
4 结束语

本文提出了一种基于微粒群辨识算法的综合负荷模型辨识方法，该方法能够有效的辨识出负荷模型的参数，并通过数字仿真实验进行了验证，实验结果能够很好的拟合负荷的有功和无功曲线，证实了该辨识算法的有效性。

[1] 周文，贺仁睦，章建，等.电力负荷建模问题研究综述[J].现代电力，1999，16(2):83-88.

[2] 程颖，鞠平，吴峰.负荷模型参数辨识的粒子群优化法及其与基因算法比较[J].电力系统自动化，2003，27(11):25-29.

[3] 张东霞，汤涌，张红斌，等.负荷模型的应用与研究调查报告[J].电网技术，2007，31(4):16-23.

[4] 石景海，贺仁睦.动态负荷建模中的负荷时变性研究[J].中国电机工程学报，2004，24(4):85-90.

[5] 鞠平，卫志农.电力负荷特性的在线测辨—模型及辨识[J].电力系统自动化，1992，16(4):15-21.

[6] PSASP7.0图模平台用户手册[S].北京:中国电力科学研究院，2007.

[7] 武朝强.电力系统动态仿真误差评价指标研究[C].华北电力大学硕士学位论文，2008.

[8] 鞠平，马大强.电力系统负荷建模(第二版)[M].北京:中国电力出版社，2008.

[9] 张进，贺仁睦.基于参数灵敏度分析的负荷建模研究[J].现代电力，2005，22(5):29-32.