计及不确定因素的梯级水电站短期优化调度

翟毅

（国电南瑞科技股份有限公司电网控制，江苏南京210061）

水电作为一种可再生能源，具有清洁环保、运行成本低廉、机组启停灵活等优点，已成为国内外首选开发能源。随着我国水电事业的快速发展,梯级水库的规模也越来越大,求解梯级水电站联合优化调度问题已成为保证电力系统安全、稳定、经济运行的一项重要课题。

电力系统中梯级水电站的短期优化调度从本质上说是一个随机优化控制问题。随着电力市场的不断发展，频繁的电能交易使系统运行的不确定性急剧增加。为保证系统的安全、可靠和经济运行，必须合理考虑不确定性因素的影响。但目前相关的研究主要集中在正常运行状态下以梯级水电站总的发电效益或蓄水量最大为调度准则，忽略了不确定因素的影响[1-7]。因此，对优化调度中所产生的不确定因素进行研究分析具有现实意义。文献[8]提出采用机会约束规划方法解决梯级水电站短期优化调度中的不确定因素问题，在协调风险和利润的矛盾中实现最优决策，文献[9]分析了引起风险的不确定因素，提出计及动态一致性风险度量的水电短期优化调度策略，文献[10]将不确定因素同经济风险结合起来形成优化调度中的约束条件，发电侧通过调整期望利润来减小运行中的经济风险，实现最优调度。

对于梯级水电站运行调度中所面临的不确定因素，如电价[11-13]、机组运行状况[14-17]、负荷突变等，需要给出度量准则。考虑到电力交易的实时性、机组故障状况的随机性、时变负荷的影响，以概率的方式协调不确定因素对经济效益带来的影响符合实际调度思想[18]。本文以概率的方式对系统安全性和经济性进行协调，分析了不确定因素的概率变化规律，通过马尔可夫链对梯级水电站机组未来调度时段的预想故障及上网电价进行概率预测，同时采用服从正态分布的负荷波动来仿真含有不确定性因素的负荷，建立了一种新的梯级水电站短期概率优化调度的模型。由于梯级水电站机组状态在数学上是一个具有离散参数和离散状态空间的问题，并且机组运行和停运的状态具有随机性，各时段机组运行不受先前机组状态的影响，因此将马尔可夫链应用到梯级水电站不确定因素的模拟中是可行的。针对该模型运用微分进化算法和蒙特卡洛方法进行求解，可得到协调风险和利润的概率调度方案，论证了模型的实用性。

1 概率调度模型的数学描述

1.1 不确定因素的模拟

电力市场环境下，不确定因素影响着梯级水电站的运行状况。本文所研究的不确定因素包括电价、机组运行状态和时变负荷。

1.1.1 机组运行状态预测

由于系统要保持安全、稳定、可靠的运行，实际调度中难免会遇到机组强迫停运的状况，这将对梯级水电站短期优化调度产生一定的影响。为构建梯级水电站的概率调度模型，本文将马尔可夫链应用到蒙特卡洛随机模拟中对机组未来运行状态进行预测，从而得到梯级水电站机组的状态样本。

{Xt：t≥0}为一随机序列，随机序列产生于条件分布{Xt∣Xt-1}，此序列是一个马尔可夫链。

当t→∞时，Xt与初始值无关，其分布趋于平稳分布，此时马尔科夫链收敛。然而在收敛的前一段时间内，如前M次采样中，各状态的密度分布还不是该平稳分布。故在估计遍历平均E[f(x)]时应该把前M个采样值去掉，而用后n-M个采样结果进行估计：

E（f）的估计值E（f）的方差为：

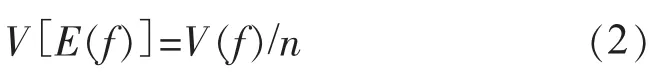
V（f）的估计值为：

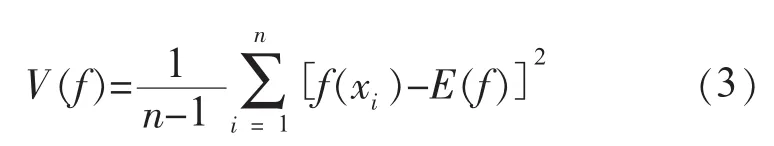
根据马尔科夫链的基本原理对未来调度时段中的机组运行状态进行预测。本文设梯级水电站机组处于运行工作的状态标记为0，处于强迫停运状态标记为1，状态模型的概率分布函数服从0-1分布，按概率p发生故障，按概率(1-p)工作，p为发电机的强迫停运率，则第i级电站机组j的状态分布为：

若将整个系统状态空间分割成2个不相交的子空间，即所有正常状态和所有故障状态组成的子空间，则故障状态子空间的概率就等于失负荷概率LOLP指标。

电量不足期望值(EENS)指在被研究的一段时间内系统电量不足的期望值。EENS对系统可靠性进行经济评估具有重要意义，是可靠性评估的重要指标。以一天为调度周期，系统电量不足期望值计算公式为：

式中：Ri为削减负荷量；pi为对应概率。

机组的运行状态是从其概率分布函数中应用蒙特卡洛方法抽样确定的，设X表示机组状态变量的集合，集合中元素个数等于梯级水电站机组总数，则对第k个样本抽样的状态变量集合为：

式中：Xki表示第k次抽样中机组i的状态；n为机组数，i=1，2，…，n。

给定所有机组的初始状态均为正常运行的情况下，与系统概率分布有关的相关概率初始值为p0，获得机组i第k+1次抽样状态Xk+1，i的方法：

(1)根据机组i目前所处的状态（0或1），从满条件分布P{Xk+1，i∣Xk/i}中得到此机组在系统当前状态下，得出下一时刻状态改变(1或0)的概率相关值p0*或p1*。

满条件分布P{Xk+1，i∣Xk/i}中，有Xk/i=｛Xk+1，1，Xk+1，2，…，Xk+1，i-1，Xk，i+1，…，Xk，n｝，其中Xk/i的前（i-1）个元素是第（k+1）次采样的抽样点，剩下的（n-i）个元素是第k次采样中的可利用的点。p0*或p1*的取值为：

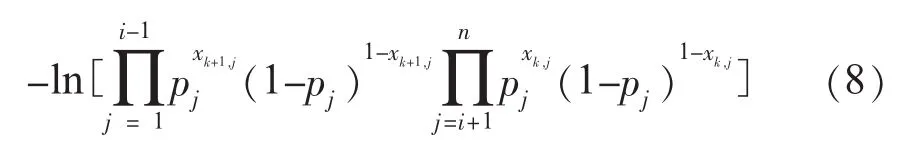
（2）计算该机组的下一个状态可能发生改变的概率：

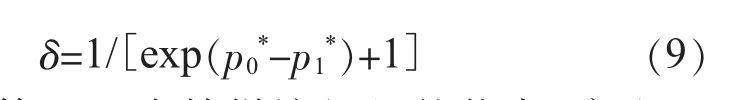
（3）确定第k+1次抽样该机组的状态，产生一个服从均匀分布U(0，1)的随机数v。

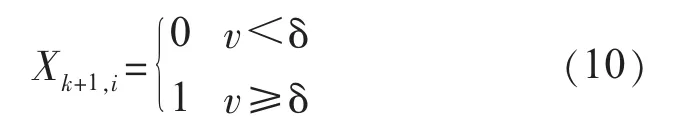
（4）如果该机组的状态发生改变，将从满条件分布中获得p0*或p1*的值作为下一个机组保持此时刻状态的相关概率。

如此循环采样，可以得到一条平稳分布为系统概率分布的马尔可夫链，利用收敛后的马尔可夫链作为电力系统的状态样本，建立概率调度模型。

1.1.2 电价预测的马尔可夫模型

在竞价上网的形势下，电价的变化主要由市场因素所引起的，诸如发电成本、电力的供求关系、市场预测等，这些随机因素使得电价呈随机走势的状态。将马尔可夫链的理论用于电价预测，从而为电价的定量分析提供技术支持。该方法的基本思想是后一时段的电价仅取决于前一时段的电价及转移概率，基本步骤如下：

（1）对电价进行状态划分。采用常数划分法，即选取有代表性的常数作为状态的界限，通常根据历史电价的最大最小值选取；

（2）计算状态的一步转移概率矩阵。尽管一步转移概率Pij的理论分布是未知的，但当样本充分大时，可以近似用状态相互转移的频率来描述。

式中：i，j=1，2，…，n，P(Ej/Ei)表示由状态Ei转移到Ej的概率；F(Ej/Ei)表示由状态Ei转移到Ej的频率。

如处于状态Ei的样本个数为Mi，由Ei转移到Ej的个数为Mij，则有：

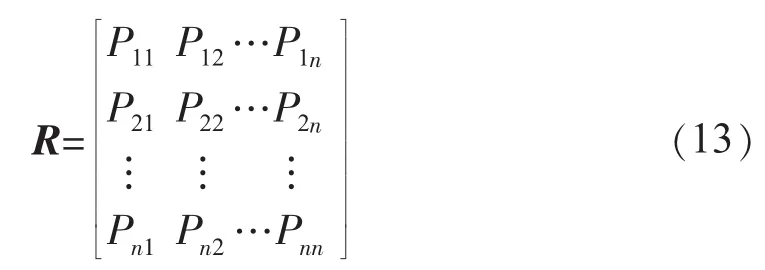
从而得出状态转移概率矩阵R为：

（3）根据一步转移概率矩阵进行预测。假定目前预测对象处在状态Ei，此时Pij就恰好描述了目前状态Ei在未来将转向状态Ej的概率。将n个概率值按大小排列，选择最大者作为预测结果，相应地把最大者对应的状态值作为预测对象在下一步的预测值。

1.1.3 时变负荷模型

由于调度期间系统中负荷同样会面临不确定因素的影响，如天气因素、节假日因素等，使得调度决策必然面对一定程度的风险，而目前对于梯级水电站优化调度问题的研究主要采用的是确定性负荷[1-9]，仅能给出确定的负荷序列。本文考虑了各种不确定性因素的影响，采用小时最大尖峰负荷与年最大负荷的比值来表示仿真时刻的负荷期望值；采用服从正态分布的负荷波动来仿真不确定性因素对负荷的影响，进而得到详细的时变负荷模型。不同调度时段负荷的期望值为：

式中：Ph（t）表示时负荷峰值占日负荷峰值的百分比；Pd（t）表示日负荷峰值占周负荷峰值的百分比；Pw（t）表示周负荷峰值占年负荷峰的百分比；Lmax表示年最大负荷。

采用标准正态分布N（0，σ2）描述负荷受多种因素影响而存在不准确性，则短期调度时段t的负荷值为：

1.2 变量约束条件

1.2.1 负荷平衡约束

式中：Ni，j（t）为梯级水电站群中第i级电站机组j在t时刻的出力；PL（t）为t时刻系统总的负荷，忽略网损。

1.2.2 水量平衡约束

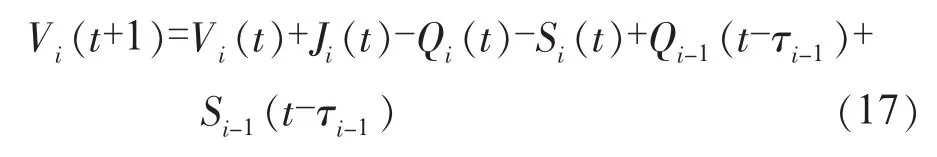
式中：Vi（t）为t时刻第i级水电站的库容；Ji（t）为t时刻第i级水电站的天然来水量；Qi（t）为t时刻第i级水电站的发电引用流量；Si（t）为t时刻第i级水电站的弃水量；τi-1为水流流达时间。

1.2.3 水库蓄水量约束

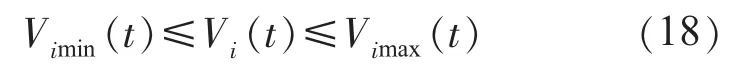
式中：Vimin（t）和Vimax（t）分别为t时段水库i应保证的最小蓄水量和允许的最大蓄水量。

1.2.4 水电机组的发电引用流量约束

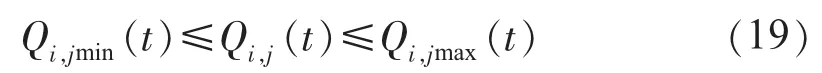
式中：Qi，jmin（t）和Qi，jmax（t）分别为t时段第i级电站水电机组j应保证的最小发电引用流量和允许的最大发电引用流量。

1.2.5 水电机组出力约束

式中：Ni，jmin（t）和Ni，jmax（t）分别为t时段第i级电站水电机组j应保证的最小出力和允许的最大出力。

1.2.6 水库水头约束

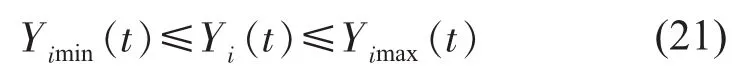
式中：Yimin（t）和Yimax（t）分别为t时段水库i应保证的最小水头和允许的最大水头。

1.3 目标函数

本文中，概率调度的目标函数为梯级水电站期望运行总收益达到最大，既考虑了电力市场中机组正常运行时的发电收益，又考虑了机组处于停运状态时对电网停止供电所赔付的费用，符合市场环境下的调度理念，即：

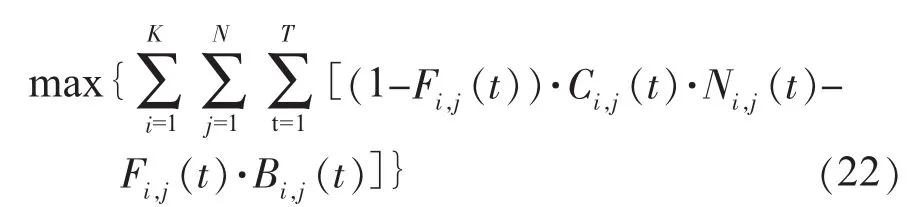
其中，

式中：K为梯级水电站中的水库总数；N为第i级水库中的发电机总数；T为时段总数；Fi，j(t)为第i级水库中机组j在t时刻的状态；Ci，j(t)为第i级水库中机组j在t时刻的市场出清电价；Bi，j(t)为第i级水库中机组j在t时刻处于强迫停机状态所赔付的费用；ηj为机组j的综合发电系数；αi，j，βi，j为赔付费用函数中相应的给定系数；Zu，i(t)为第i级水库在t时刻的前池水位；Zd，i(t)为第i级水库在t时刻的尾水位；au，i，bu，i，cu，i为第i级水库前池水位的特征系数；ad，i，bd，i，cd，i为第i级水库尾水位的特征系数。

2 求解方法及步骤

2.1 微分进化算法（DE）

DE是由Storn和Price在1995年提出的一种高效率的智能优化计算方法。该算法源于遗传算法，但由于不需进行编码和解码操作，使用上大为简化，同时它对初始值无要求，收敛速度快，对各种非线性函数适应性强，尤其适应于多变量复杂问题的寻优。对解决梯级水电站优化调度这类高维、非凸的、有时滞的、非线性的优化问题非常有效。该算法中的寻优基本步骤如下。

（1）变异。第k次迭代中变异向量Vik+1的分量产生方式为：

式中：Irand是从[1，D]中随机选取的一个整数，用以保证本次操作必须有一位经过交叉，D为向量的维数。交叉因子CR控制着种群的多样性，避免算法陷入局部最优。

（3）选择。当且仅当新个体的评价函数值更好时，才能被保留到下一代群体中，否则，父个体仍然保留在群体中，再一次作为下一代的父向量。选择方式为：

2.2 模型的求解步骤及流程图

（1）算法参数初始设置。设置种群规模N，输入问题的空间维数D，最大迭代次数E及控制参数F和CR的取值等。

（2）种群初始化。将梯级水电站中的各级电站中机组的发电引用流量作为决策变量。在控制变量变化范围内随机生成N个解，形成种群A，并设当前迭代次数k为1。

（3）根据历史电价资料，应用马尔可夫模型对未来调度时段中的电价进行预测。

（4）采用马尔可夫链对未来各调度时段的梯级水电站机组运行状态进行预测，应用蒙特卡洛方法随机抽样M次，可得到一条平稳分布对应于机组状态的马尔可夫链。

（5）根据式（22）计算每一个个体的目标函数值，以此为基础，对违反约束条件的个体采用惩罚函数方法计算个体的目标适应度，而不违反约束条件的个体，直接将其目标函数值作为目标适应度。取其中目标适应度最大值作为群体当前的最优解。

（6）判断当前迭代次数k是否到达最大迭代次数E，若不满足条件，置迭代次数k=k+1；若满足条件，转至步骤（8）。

（7）根据步骤（5）的结果，采用微分进化算法对种群进行变异、交叉、选择操作，得到新一代的种群A'，返回步骤（5）。

（8）输出全局最优解，从而得到梯级水电站最优调度方案。算法求解流程见图1。

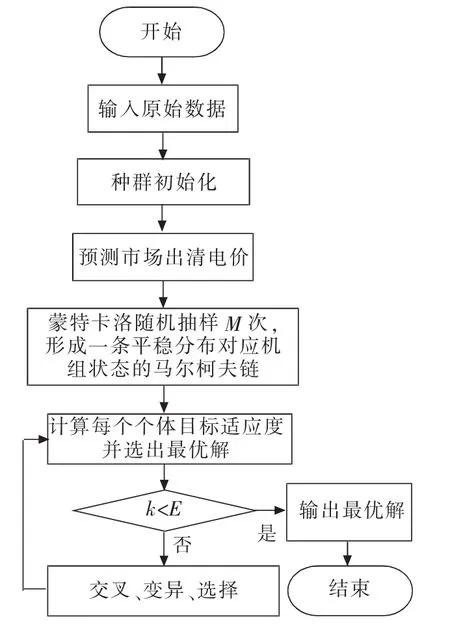
图1 算法求解流程图

3 算例及其分析

以一3级梯级水电站系统为例验证本文提出的模型和算法。其中上游水电站A为年调节性电站，B电站和C电站为季调节性电站，调度周期为24h，1h为一个时段。系统相关数据见表1和表2，本文考虑了梯级水电站群运行中变水头的影响和连续两级水库之间所形成水流时滞的影响。梯级水电站中各级电站的初库容为前一调度周期的末库容，本文中各库容初始值分别为7.81亿m3、6.45亿m3、6.78亿m3。在本文的微分进化算法中各参数的取值为：算法的群体规模N=50；最大进化代数E=200；蒙特卡洛抽样次数为1000；比例因子F和交叉因子CR的取值分别为0.7和0.5。根据表1和表2中的相关数据梯级水电站中各级电站中机组的最大发电引用流量可以由式（23，25，26，27）计算得到。算法采用MATLAB编程实现。

表1 水电机组参数

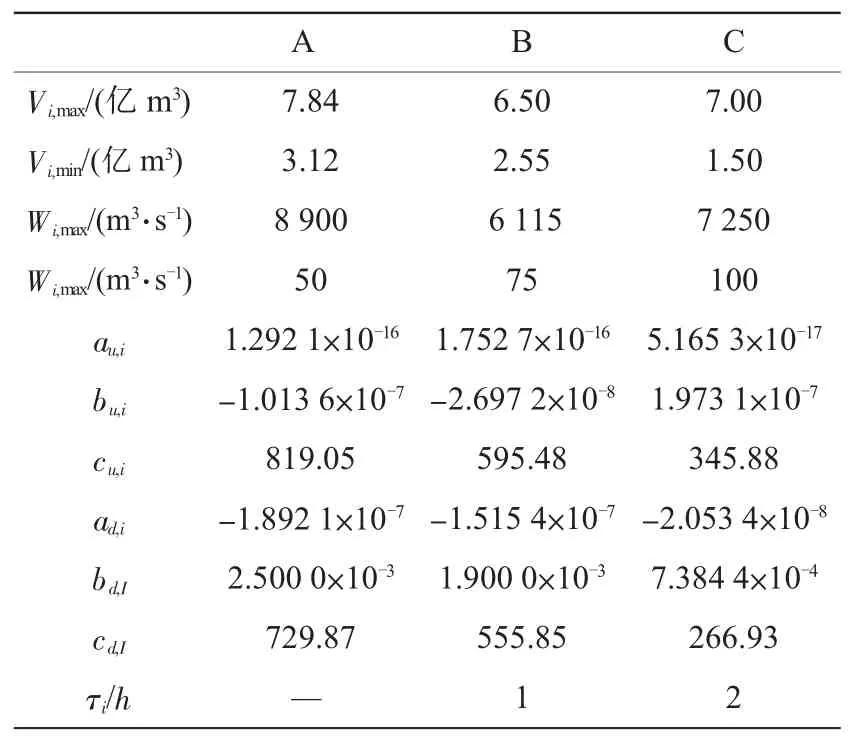
表2 水库的参数

表1中pj和pg,j分别表示确定性负荷和时变负荷状况下机组的强迫停运率，表2中Wi,max，Wi,min表示梯级水电站中第i级水库的最大下泄流量和最小下泄流量。

文献[19]表明采用马尔可夫模型预测电价具有较高的准确性，故文中依此得到计划交易日市场出清价的预测值如图2所示，然后根据预测电价进一步的求取梯级水电站概率调度模型的最优解。图3给出短期优化调度中确定性负荷和时变负荷的变化曲线，由于考虑负荷中不确定因素的影响，因此本文在确定性负荷的基础上，采用满足标准正态分布的负荷波动仿真系统中负荷不确定因素，进而得到时变负荷的变化曲线。

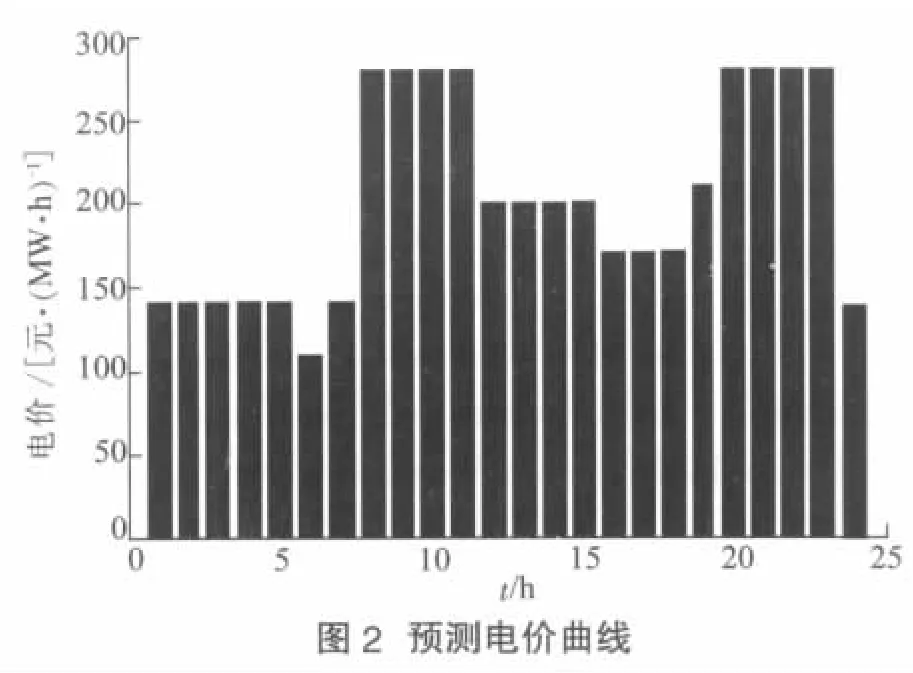
图3 短期负荷预测曲线

基于所得到调度时期内各时段的电价、机组运行状态、时变负荷，全面分析梯级水电站中各种约束条件的限制，按照3种方案对短期概率模型求解，即方案1为确定性负荷下不计机组停运状态的优化调度方案；方案2为确定性负荷下计及机组停运状态的优化调度方案；方案3为时变负荷下计及机组停运状态的优化调度方案。数据结果见表3。

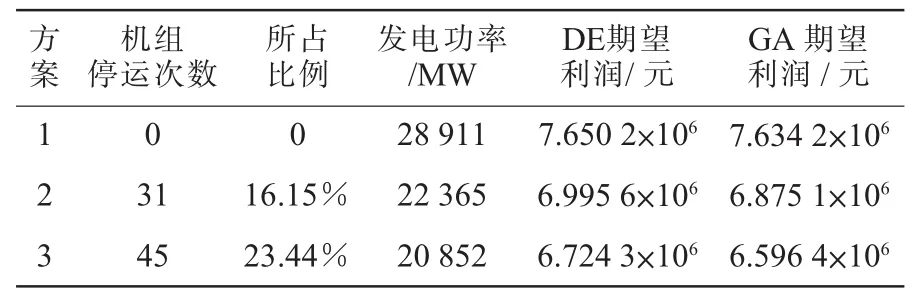
表3 不同方案下的调度结果与分析

表3中列出了不同方案下以期望运行效益最大为目标的概率优化调度结果，同时分别应用DE算法和遗传算法(GA)对模型求解，结果表明DE算法在寻找全局最优解方面优于GA。其中，具体给出了调度周期内所有机组停运的次数、停运机组的状态数占整个调度周期内机组运行状态的比例、调度周期内梯级水电站发电总功率及其期望获得的利润。调度结果表明不确定因素对于梯级水电站短期优化调度的研究有着较大的影响，不确定因素越多，系统面临的风险就越大，相应的经济效益会有所降低。

表4 几种方法对梯级电站可靠性指标计算结果比较

从表4中可以看出，本文方法对于可靠性指标LOLP和EENS结果非常相近，说明了本文方法的有效性；采样成功率和LOLP相对误差结果表明本文所采用的方法能够快速收敛，减少采样次数。

4 结束语

本文采用马尔可夫链理论对未来调度时段的电价和机组运行状态进行预测，考虑了中断供电后发电侧对用户的赔偿费用，通过分析确定性负荷和时变负荷对梯级水电站短期优化调度的影响，构建了不确定因素的梯级水电站短期概率优化调度模型。将电力系统可靠性理论与优化调度相结合，扩展了传统电力系统调度的概念，在期望发电效益最大化下，实现了电力市场机制下的梯级水电站短期优化调度的最优决策。

[1] 蔡兴国，林士颖，马平.现货交易中梯级水电站竞价上网的研究[J]．中国电机工程学报，2003，23（8）：56-59.

[2] RODRIGUES R N，FINARDI E C，da SILVA E L.Optimal Dispatch of Hydro Generation Plants Via Augmented Lagrangian[C].Power Engineering Society General Meeting,2005(3)：2732-2737.

[3] ANTONIOL J M,FRANCISCO APOLINARV.Self-scheduling of a Hydro Producer in a Poolbased Eelectricity Mmarket[J].IEEE Transcations on Power System,2002,17(4)：1265-1271.

[4] 费君如，董增川，王德智，等.改进加速遗传算法在梯级水电优化化调度中的应用[J].水力发电.2008，34(8)：8-11.

[5] 谢红胜，吴相林陈阳，等.分时电价下梯级水电站间短期优化调度仿真[J].华中科技大学学报（自然科学版），2008，36（3）：114-117.

[6] LAKSHMINARASIMMAN L,SUBRAMANIAN S.Shortterm Scheduling of Hhydrothermal Power System with Cascaded Reservoirs by Using Modified Differential Evolution[J].IEEProc.-Gener.Transm.Distrib，2006，153（6）：693-700.

[7] 刘自发，张建华.一种求解电力经济负荷分配问题的改进微分进化算法[J].中国电机工程学报，2008，28(10)：100-105.

[8] 吴杰康，朱建全.机会约束规划下的梯级水电站短期优化调度策略[J].中国电机工程学报，2008，28（13）：41-46.

[9] 刘嘉佳，刘俊勇，帅颖，等.计及动态一致性风险度量的水电短期优化调度[J].中国电机工程学报，2008，28（10）：94-99.

[10] WU L,LI Z Y.GENCO’s Risk-constrained Hydrothermal Scheduling[J].IEEE Transactions on Power Systems,2008,23(4)：1847-1858.

[11] VERBIC G,CAIZARES C A.Probabilistic Optimal Power Flow in Electricity Markets Based on a Two-point Estimate Method[J].IEEE Trans on Power Systems,2006,21(4)：1883-1893.

[12] LI T,SHANIDEHPOUR M,LI Z.Risk-constrained Bidding Strategy with Stochastic Unit Commitment[J].IEEE Transactions.Power Systems,2007,22(1)：449-458.

[13] JABR R A.Robust Self-schduling Under Price Uncertainty Using Conditional Value-at-risk[J].IEEE Transactions on Power Systems,2005,20(3)：1852-1858.

[14] Wu L,SHAHIDEHPOUR M,LI T.Cost of Reliability Based on Stochastic Uunit Commitment[J].IEEE Transactions.Power Systems,2008,23(3)：1364-1374..

[15] 李庚银，高亚静，周明.可用输电能力评估的序贯蒙特卡罗仿真法[J].中国电机工程学报,2008,28(25)：74-79.

[16] 石文辉，别朝红，王锡凡.大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J].中国电机工程学报,2008,28（4）：9-15.

[17] 赵渊，沈智健，周念成，等.大电网可靠性蒙特卡洛仿真的概率不确定分析[J].中国电机工程学报,2008,28(28)：61-67.

[18] 查浩，韩学山，杨朋朋.电网运行状态下的概率优化调度[J].中国电机工程学报，2008，28（28）：54-60.

[19] Alicia Mateo González,Antonio Munoz San Roque.Modeling and Forecasting Electricity Prices with Input/Output Hidden Markov Models[J].IEEE Transactions on Power Systems，2005（2）：13-23.