基于原对偶解耦内点法的节能减排多目标动态优化调度研究

张焱，王艳，王磊

（1.东南大学电气工程学院，江苏南京210096；2.常州供电公司，江苏常州213003）

动态优化调度是研究在连续多个时间段内、机组运行状态已经确定的情况下，如何有效地调整各个机组在不同时段的有功功率输出，使得在满足各种静态约束和动态约束下，整个调度周期内的某些目标函数达到最优。由于动态优化调度问题的规模随着系统规模以及时段数的增加而迅速增长，因此提高算法的效率是迫切需要解决的问题［1］。

多年来，学者们通过不断探索，提出了各种求解优化调度问题的计算方法。其中，简化梯度法具有简单、容易实现等优点，但是收敛性较差，尤其是在接近最优点附近时收敛很慢［2］；牛顿法和简化梯度法相比，收敛速度较快，具有二阶收敛性，但是也存在着数值不稳定、不能总是有效地确定迭代过程中起作用的约束集等缺点；人工智能算法对函数的性态要求比较低，近年来在最优潮流领域中得到了广泛的运用［3］，但是存在着收敛速度比较慢的缺点。相比于以上算法，原对偶内点法具有迭代次数与系统规模关系不大、收敛性好、计算速度快等优点。文献［4］将原对偶内点法应用于非线性规模的无功优化调度问题，充分显示了内点法的收敛特性；文献［5］则采用线性约束网络流来描述电力系统动态经济调度问题，并用内点法进行求解，克服了传统方法难以精确处理不等式约束的弊端，使计算结果更精确；文献［6］则采用引入离散惩罚的非线性原对偶内点法求解动态无功优化模型，具有较快的计算速度。

随着电力行业节能减排政策的实施，在动态优化调度中同时将煤耗和污染物排放一起优化更具现实意义［7］。本文首先建立了同时考虑调度周期内煤耗量、污染物气体排放量最小的多目标动态优化调度模型，并利用模糊集理论使之转化为求取满意度最高的单目标问题；接着推导出了求解该模型的原对偶解耦内点算法；最后对算例结果进行了比较分析。

1 基于节能减排的多目标动态优化调度模型

1.1 多目标动态优化调度模型

1.1.1 目标函数

本文以常规燃煤机组的煤耗和污染物气体排放最小作为目标函数：

式(1，2)中：T为调度周期；Ng表示发电机台数；PGi(t)为第i台发电机组t时段的有功出力；ai，bi，ci为煤耗系数；αi，βi，γi为污染物排放系数。

1.1.2 静态等式约束

动态优化调度问题的静态等式约束即为各个时段的节点潮流平衡约束：

式中：省略下标t；Vi，θi为节点电压与相角；θij=θi-θj；Gij，Bij分别为系统的导纳矩阵的实部与虚部；PDi，QDi为节点i的有功负荷与无功负荷；PGi，QGi为节点i的有功注入与无功注入。

1.1.3 静态不等式约束

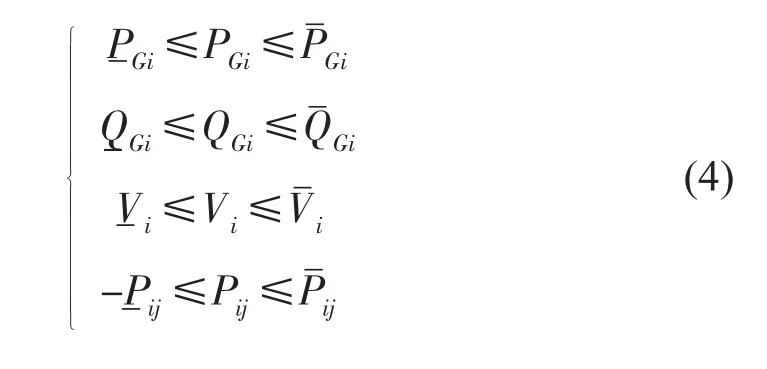
式中不等式约束依次为发电机有功出力约束、发电机无功出力约束、节点电压约束、线路有功潮流约束。各个变量的上下限且分别用上划线和下划线表示。

1.1.4 动态约束

本文考虑发电机爬坡约束：

式中：RampGi为发电机在相邻时段间能增加或减小的最大功率。

1.2 多目标动态优化调度的模糊模型

上述模型有2个相互竞争的目标函数，是多目标规划模型，有学者提出用模糊集理论来解决这个问题，并取得较好效果。文献［8］用模糊集理论将多目标函数和部分可伸缩的约束条件模糊化，使最优潮流问题在更加符合实际情况的模型上实现优化；文献［9］将模糊集理论应用于来水量不确定性分析，提出了一种水火电系统短期经济调度的新方法，较好地提高了系统的经济性；文献［10］用多目标模糊优化理论和动态规划法解决火电厂多目标负荷优化问题，得到科学、合理的负荷分配方案。因此，本文采用模糊集理论使多目标动态优化调度转化为单目标问题。在满足所有约束条件的前提下，发电煤耗和污染物气体排放总量越小越好，有上限而无下限，因此选用降半直线作为它们的隶属度函数［11］，如图1、图2所示。

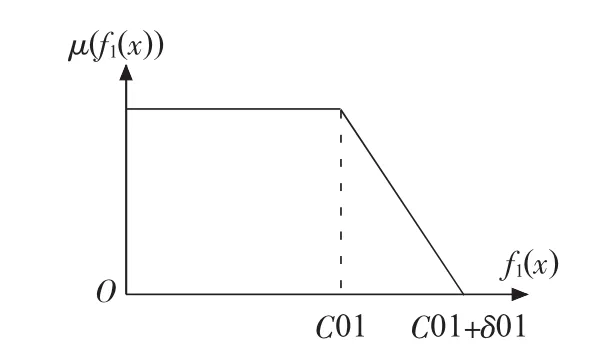
图1 煤耗隶属度函数

图2 污染物气体排放隶属度函数

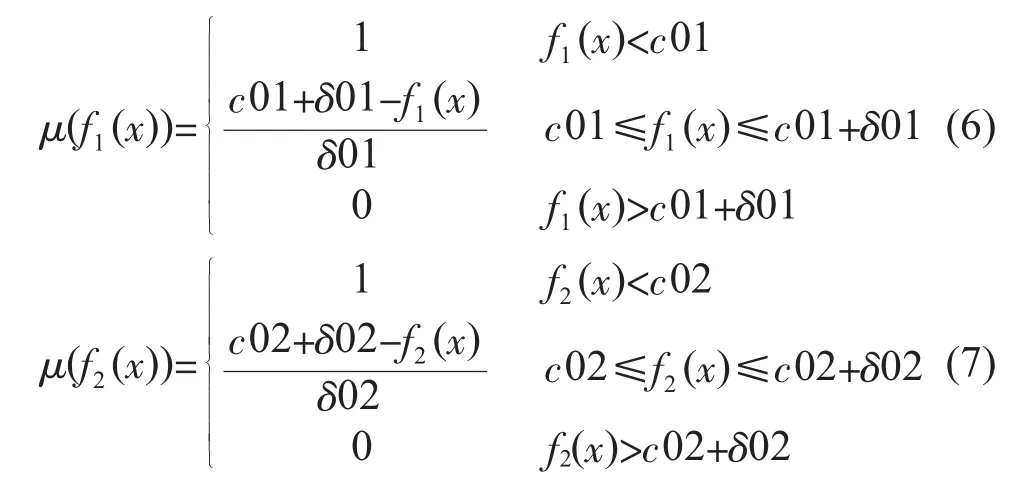
2个目标隶属度函数可分别用式（6，7）表示：式中：f1(x)，f2(x)分别为调度周期内的煤耗、污染物气体排放总量；c01，c02分别为单独以煤耗、污染物气体排放为优化目标时的结果；c01+δ01，c02+δ02分别为煤耗、污染物排放的最大可接受值。取λ为所有隶属函数中最小的隶属变量，可称之为满意度。

根据最大隶属度原理，可以将原来的多目标动态优化调度问题转化为满足所有约束条件的满意度最大化的问题。用以下非线性规划模型表示。

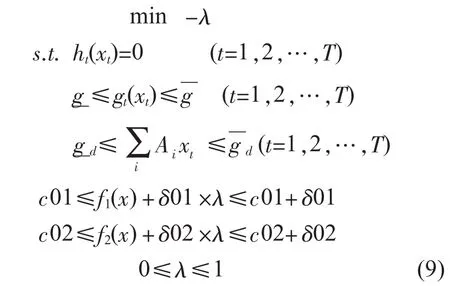
上述模型包含T个时段，每个时段有n个变量、m个静态等式约束、r个静态不等式约束，各时段间有q个动态不等式约束，p个含有λ的不等式。多目标动态优化调度的模糊模型比传统动态优化调度模型增加了p个含有λ的不等式，λ不属于静态变量，因此求解该模型时更为复杂。

2 原对偶解耦内点算法

由于动态优化调度问题系统规模很大，而原对偶内点法具有迭代次数与系统规模关系不大、收敛性好、计算速度快等优点，因此本文采用原对偶内点法求解多目标动态优化调度模型。根据多目标动态优化调度模型的特点，对原对偶内点算法作出相应改进，通过对算法中修正方程的降阶与解耦，将动态优化调度的大规模线性修正方程的求解，等值解耦转换成小规模的动态变量求解和各时段静态变量求解，从而提高算法的求解效率。

2.1 引入满意度后的修正方程

式中：yt为各时段静态等式约束对应的拉格朗日乘子，各时段静态不等式约束对应的松弛变量为lt，ut＞0，拉格朗日乘子为zt＞0，wt＞0，对数壁垒参数μt＞0；动态约束对应的松弛变量为sl，su＞0，拉格朗日乘子为yl，yu＞0，对数壁垒参数μd＞0；含有λ的不等式的松弛变量为ll，uu＞0，拉格朗日乘子为zz＞0，ww＞0，对数壁垒参数。

为了表述方便，将各时段的优化变量以及与静态约束相关的拉格朗日乘子和松弛变量构成静态变量ρt=[xt，yt，zt，wt，lt，ut]T，每个时段的静态变量一共构成T组静态变量；定义与动态约束相关的拉格朗日乘子和松弛变量为动态变量ρd=[λ，yu，yl，su，sl，ww，zz，uu，ll]T。

原对偶内点法通过式(10)的最优性KKT条件形成一组非线性方程，然后采用牛顿法迭代求解。其中，线性化牛顿修正方程可以表示如下：

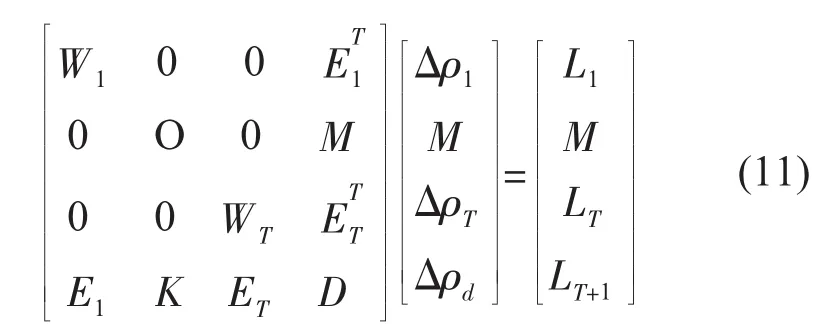
式(11)中：Wt、Lt推导过程参照文献［13］，修正方程的维数高达(4r+m+n)T+4(q+p)维，需进行降阶。

2.2 修正方程的降阶

通过线性变换消去方程(11)中的Δzt，Δwt，Δlt，Δut，Δsu，Δsl，Δuu，Δll后得到：

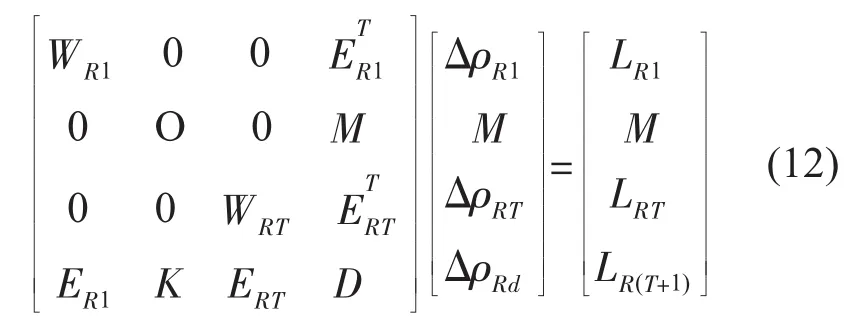
式中：ΔρR1=[Δxt，Δyt]T，ΔρRd=[Δλ，Δyu，Δyl，Δww，Δzz]T，各子矩阵WRT、LRT推导过程也可参照文献[13]。求出ΔρRT，ΔρRd后，可以通过线性变换求出其他变量。降阶后的修正方程维数为(m+n)T+2(q+p)，大大减少了方程规模和计算量。

2.3 修正方程的解耦

由多目标动态优化调度的模型可知，各时段的静态约束和目标函数相互独立，相应地静态变量ρt相互独立，彼此不相关，从而使得式(11)中常数项Lt只与t时段的静态变量有关，与动态变量无关，且Δρt之间的关联系数矩阵为零矩阵；另一方面，动态约束使部分静态变量（各时段的发电机有功出力）与动态变量相互关联，因此式(11)中Δρt与Δρd之间的关联系数矩阵Et非0。由此可以得出，多目标动态优化调度问题的特殊耦合关系决定了式(11)的系数矩阵具有分块对角带边结构，降阶KKT方程(12)的系数矩阵也同样具有分块对角带边结构。针对这种特性，可以通过线性变换将式(12)等值简化成解耦方程［14］：

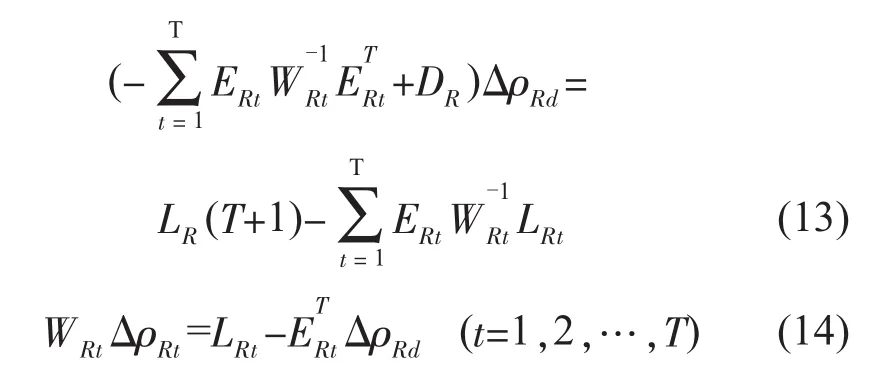
首先根据式(13)解出ΔρRd，然后分别求出各个时段的ΔρRt。解耦后，需要求解一个2(q+p)维方程和T个(m+n)维方程，计算量比直接求解一个(m+n)T+2(q+p)维方程要小得多。

2.4 相关参数设置

所有的对数壁垒参数都由式(15)求得，静态变量中原变量、对偶变量对应的步长根据式(16)计算，各动态变量对应步长αpd，αdd，αpλ，αdλ的计算方法同式(16)。

2.5 算法流程

算法流程如图3所示。

3 算例分析

根据上述模型和算法，本文对IEEE-30节点测试系统进行仿真计算与分析。

3.1 初始条件设置

调度周期取为一天，划分成24个时段，每个时段为1h，图4为负荷波动系数曲线，假设系统有功功率日负荷波动曲线和无功功率日负荷波动曲线是相同的，并且各节点的负荷值在一天中以相同的负荷系数波动。各常规发电机组的煤耗系数ai，bi，ci和污染物气体排放系数αi，βi，γi如表1所示。本文以煤耗费用（元）来表征煤耗量，以排放气体的重量（t）来表征污染物气体的排放量。

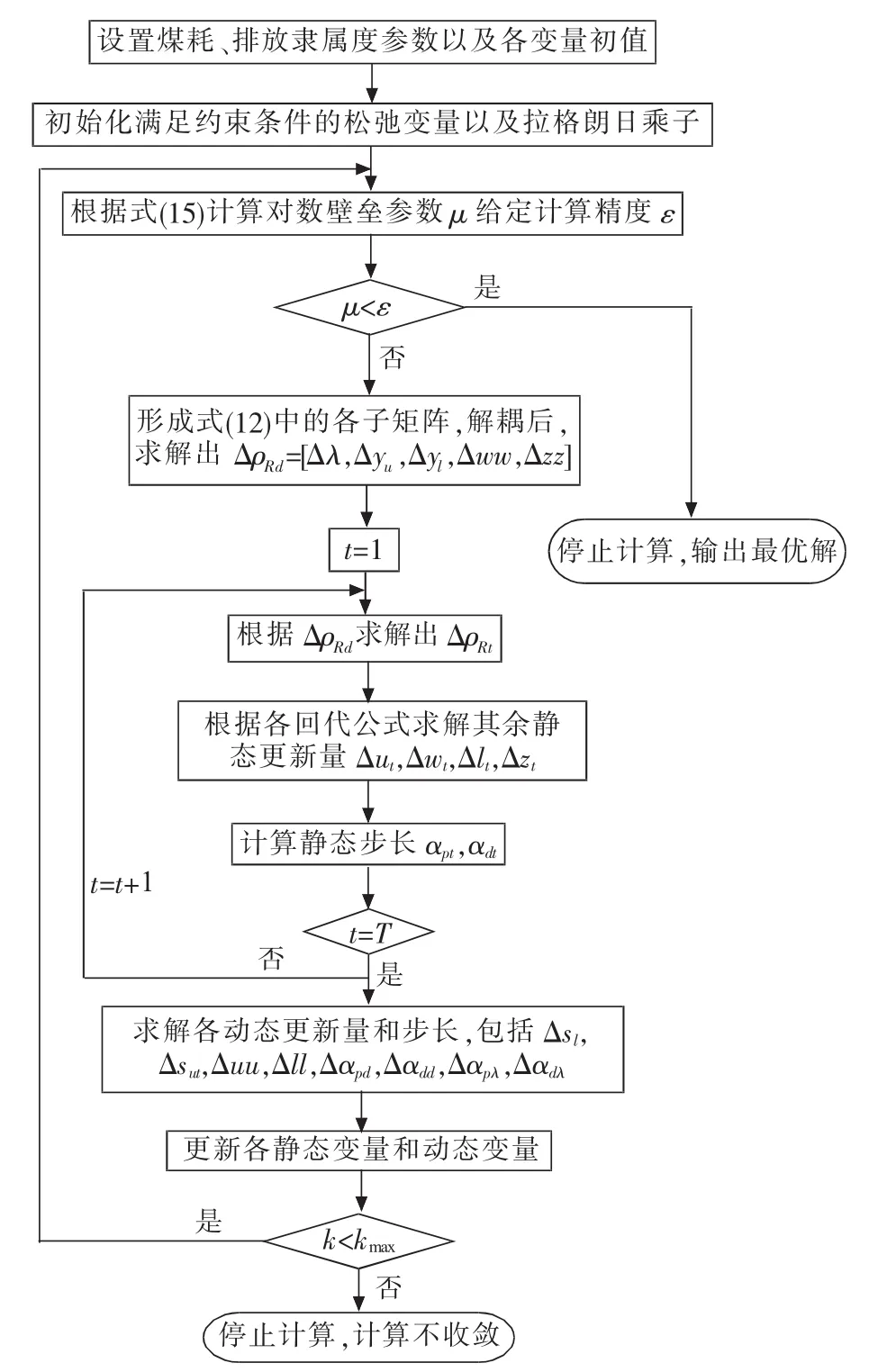
图3 原对偶解耦内点法的具体流程图

表1 各常规机组煤耗和污染物气体排放系数

图4 系统日负荷波动系数曲线

以发电机有功功率上限的百分比来表示爬坡约束，本文取为5%。

单独优化煤耗的结果为10502元，单独优化污染物气体排放时结果为3660.2t，取各自的最大可接受值为单独优化结果的1.4倍。

3.2 动态与静态优化调度结果对比分析

本文首先选取调度周期内煤耗量最小为单目标进行优化调度，图5比较了当爬坡约束为5%和未考虑爬坡约束时的27号发电机有功出力，即动态优化调度和静态优化调度时27号发电机有功出力变化的不同。

图5 27号发电机有功出力变化曲线

由图5可以看出：计及爬坡约束时，为了可以顺利到达12点时的负荷高峰，27号发电机组在第5时段作出了相应的调整，第5时段系统的负荷水平降低，但是此时煤耗较小的27号发电机就开始增加出力，从第6时段开始则全力爬坡，以保证在12点的高峰期能够承担更多的负荷；同样，为了应付22-24时段负荷的陡降，即使是在21-22时段负荷上升的情况下，27号发电机仍然减少了出力，并在23、24时段全速减小出力，保证系统能够顺利到达负荷的低点。

而如果未考虑爬坡约束，在12点负荷高峰前的多个爬坡时段和负荷陡降的22-24时段，27号发电机有功出力调节速率均超出了允许范围。由此可见，静态优化调度的结果显然是不可行的，只有动态优化调度的结果才是正确有效的。

3.3 双目标优化与单目标优化结果对比分析

图6显示了双目标优化时，各时段的煤耗量与污染物气体排放量都比单目标时的优化结果大。这是因为考虑多目标时，不仅要使得系统煤耗量最小，同时还要使污染物气体排放量最小，但这2个目标是相互矛盾的，污染物气体排放满意度的增加必然要以煤耗满意度的下降来换取，反之亦然，因此只能使得两者的综合满意度达到最高。

表3比较了双目标与单目标时整个调度周期内的总煤耗量和污染物气体总排放量。

图6 双目标与单目标各时段优化结果对比

表3 双目标优化和单目标优化目标值比较

从表3可以看到，双目标优化之后，煤耗量比单独优化煤耗时增加了256元，相对增长2.44%，但比单独优化排放时的煤耗量减少了498元，相对减少4.42%；同样，双目标优化之后，污染物气体排放量比单独优化排放时增加了89.4 t，也仅相对增长2.44%，但比单独优化煤耗时的排放量减小了461.3 t，相对减小10.95%。

由此可见，虽然调度周期内的总煤耗量和排放量都没有单目标模型时的理想，但从综合效益的角度看，基于节能减排的多目标动态优化调度模型具有明显的优势，它能够更加合理的协调各个目标之间的关系。

4 结束语

本文以节能、减排作为动态优化调度的双重目标，建立了多目标动态优化调度模型，并根据模糊集理论的最大隶属度原则使之转化为求解满意度最大的单目标问题，提出了适合求解多目标动态优化问题的原对偶解耦内点算法。IEEE-30节点算例结果表明：

（1）本文通过对原对偶内点法中修正方程的降阶与解耦，大幅度提高了算法的求解效率，收敛特性较好，数值鲁棒性高。

（2）本文提出的基于节能减排的多目标动态优化调度模型能够更好的协调节约能源、减少环境污染之间的关系，并能根据机组的煤耗特性、排放特性以及爬坡约束等更加合理的安排发电机组的出力，在整个调度周期内实现各个目标函数综合满意度的最大化。

（3）本文所提的模型与算法不仅适合于双目标动态优化调度问题，还能根据实际情况灵活扩展到更多的目标函数。

［1］ 覃智君，阳育德，吴杰康.矢量化动态最优潮流计算的步长控制内点法实现[J].中国电机工程学报，2009，29(7)：52-58.

［2］ 张伯明，陈寿孙，严正.高等电力网络分析（第2版）[M].北京：清华大学出版社，2007.

［3］ IMMANUEL SELVAKUMAR A，THANUSHKODI K.A New Particle Swarm Optimization Solution to Nonconvex Economic Dispatch Problems[J].IEEE Transactions on Power Systems,2007,22(1)：42-51.

［4］ GRANVILLE S.Optimal Reactive Dispatch Through Interior Point Method[J].IEEE Transactions on Power Systems,1994,9(1)：136-146.

［5］ 李秀卿,罗忠游,郭芳义.基于网络流和内点法的电力系统动态经济调度[J].继电器，2006，34(10)：37-40.

［6］ 赖永生,刘明波.电力系统动态无功优化问题的快速解耦算法[J].中国电机工程学报，2008，28(7)：32-39.

［7］ 冯士刚，艾芊.火电站多目标负荷调度及其算法的研究[J].动力工程，2008，28(3)：404-407.

［8］ 刘明波,段晓军,赵艳.多目标最优潮流问题的模糊建模及内点解法[J].电力系统自动化，1999，23(14)：37-40.

［9］ 艾琳，华栋.基于模糊优化和内点法的水火电系统短期经济调度[J].电力自动化设备，2008，28(8)：46-50.

［10］ 冯培燕.基于模糊多目标优化的火电厂负荷优化分配研究[D].北京:华北电力大学，2007.

［11］ 马瑞，穆大庆，李欣然.电力市场中日有功负荷多目标分配模糊决策的研究[J].电网技术，2001，25(2)：25-29.

［12］ XIE K,SONG Y H.Optimal Power Flow with Time-related Constrains by a Nonlinear Interior Point Method[A].Proceedings of 2000 IEEE Power Engineering Society Winter Meeting[C].Singapore，2000.

［13］ 王锡凡，方万良，杜正春.现代电力系统分析[M].北京：科学出版社，2003.

［14］ XIE K，SONG Y H.Dynamic Optimal Power Flow by Interior Point Methods[J].IEE Proceedings：Generation,Transmission and Distribution，2001，148(1)：76-84.