C3和C5航线远期运费波动溢出效应实证研究＊

朱意秋 陈先洋

(中国海洋大学经济学院,山东 青岛 266100)

一、引言

远期运费协议(Forward Freight Agreements,简称FFA)市场于1991年在英国伦敦创设,是一种柜台交易(OTC)的航运衍生品。协议由当事人双方直接或者在经纪人撮合下成交。协议中规定具体的船型、航线、合约价格、数量和到期日等,规定在每月底或到期日后收取或支付结算价格与合约价格的差额①。国内外研究FFA与航运实体市场间波动溢出的文章不多,国外文献中只能检索到 Kavussanos等人在2004年发表的“M arket interactions in returns and volatilities betw een spot and forward shipping freight markets”一文。[1]该文选用上世纪主力船型——巴拿马船和涉欧航线P1、P1A、P2和P2A作为研究对象,数据区间从1997年1月至2000年7月,数据类型是即期价格和 FFA的1个月远期。该文的主要结论是：波动在即期和远期两个市场之间的传播因航线而异；航线P1、P2和P2A是双向传播的,而航线 P1A在波动上没有任何传播。目前尚没有检索到国内学界对FFA市场波动溢出的研究文章。

本文将选择本世纪国际干散货,尤其是铁矿石的主力船型—好望角型船,并选择与中国相关的两条航线—C3和C5,借助于Eview s 6软件进行远期运费市场与即期实体航运市场间波动溢出效应的实证研究。

二、波动溢出模型

波动溢出理论认为,一个市场的波动不仅受到自身前期波动的影响,还受到其他市场前期或当期波动的影响。熊正德和谢敏全面评述了金融市场间波动溢出效应的理论和方法,[2]按其分类,本文将在GARCH基础上采用单变量和双变量两类均值方程研究FFA与即期市场间波动溢出效应。以A市场均值方程的残差平方作为波动溢出因子项代入B市场条件方差方程(即波动方程)中,计算其系数并观察其统计显著性,从而确定A市场是否向B市场传播了波动信息。

(一)单变量均值方程—GARCH模型

1990年,Y.Hamao等运用 M A(1)-GARCH (1,1)-M模型研究了纽约、东京和伦敦三地股市间价格波动溢出的特性,[3]其两步计算波动溢出因子系数的方法经常被后学仿照,实证步骤和模型如下：

1、提取均值方程误差εit

在验证三地股市收益率序列均存在ARCH效应后,Hamao运用如下公式获取均值方程残差。

i分别代表纽约、伦敦和东京股票市场。Rit表示收益率均值方程,εit为均值方程残差，受前一时间信息Fit-1的影响，服从均值为0方差为的分布，为波动方程。

2、计算波动溢出因子f

将εit加入到另一个市场扩展的MA-GARCHM模型中,得到溢出因子系数及其统计检验,溢出因子波动方程如式(3)所示。

i,j均代表各个市场，但i≠j。f是溢出因子系数，该值越大，表示j市场对i市场的波动溢出影响越大。

(二)双变量均值方程—EGARCH模型

Laopodis采用VAR-EGRACH模型研究了德国马克在不同汇率间的波动溢出,[4]张金清和刘庆富利用了V EC-EGARCH模型研究了中国金属期货市场和现货市场之间的波动性关系。[5]我们将采用V ECM和VAR两种模型作为EGARCH的均值方程。以V EC-EGARCH模型为例,实证步骤和公式如下：

1、提取均值方程残差εst和εft

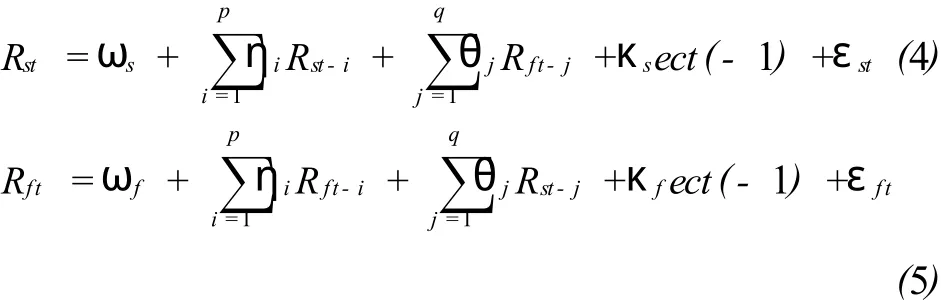
式中,s和f分别代表即期和远期市场,R为均值方程,η为自身滞后项系数,θ为另一个市场滞后项系数,ect为误差修正项,κ为误差修正项系数,ε为残差。

2、计算波动溢出系数ρs和ρf

式中,ψ表示新信息对波动的冲击力度,τ是信息冲击的不对称效应参数,φ描述波动的“集聚性”。如上参数对于研究收益率波动特征都有很重要的意义，本文因重点研究市场间的波动溢出效应所以不对上述参数进行分析。ρ为溢出系数,表示另一市场溢出效应的大小。

三、数据及其检验

C3和C5均是好望角船干散货程租航线,载重为15～17万吨,主要用作铁矿石运输,即期和远期市场的报价形式均为美元/吨,C3航线从巴西的图巴朗到中国北仑或宝山,C5航线从西澳大利亚至中国北仑或宝山。

(一)数据来源

本文所使用的价格数据均来自伦敦波罗的海航运交易所。该所每天下午四点向各会员单位发送当天的即期和远期数据。即期价格根据租船市场的真实交易报出,远期价格则由交易所根据各个航运咨询公司的成交情况综合算出,如果某个衍生品种当天没有交易则由专家根据经验估计得出,数据类型称为BFA(Baltic Forward A ssesment)。表1是C3航线2011年1月16日的BFA数据,除即期价格外还有当月、未来1个月等6个月份的远期、4个季度的远期和数个年份的远期等12种。

表1 BFA即期和远期价格类型

本文所用的数据为2006年1月3日至2010年11月30日,除即期价格外,远期品种只选用了当月(f0)、1个月期(f1)和2个月期(f2)三种。除掉一些数据不合要求的日期后,C3获得1177天共计4708个数据,C5获得1189天共计4756个数据。

C3和C5航线近5年来的即期和三种远期价格走势如图1和图2所示,纵坐标单位为美元/吨,横坐标为数据序列号,最高点对应着2008年5、6月份,最低点对应着2008年12月末。

(二)收益率统计性描述及自相关检验

实证中将原始数据先对数化再差分后获得了各期运价的收益率序列,收益率序列的统计性描述和滞后4期的自相关检验如表2所示。

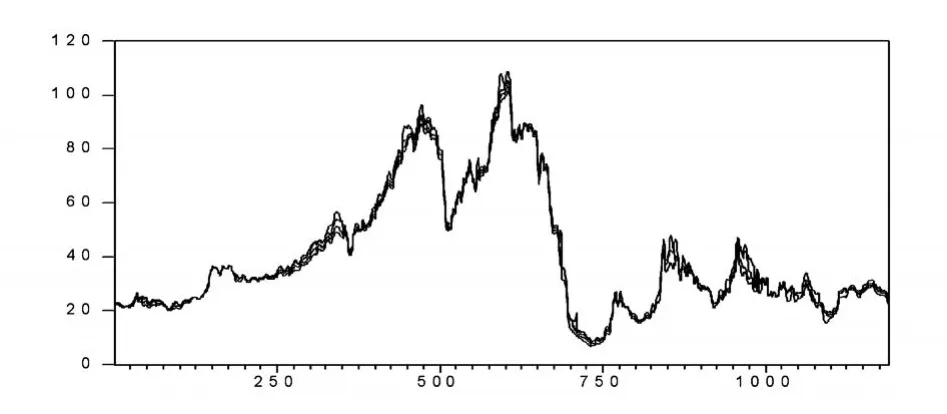
图1 C3航线现货和远期价格走势

图2 C5航线现货和远期运费价格走势图

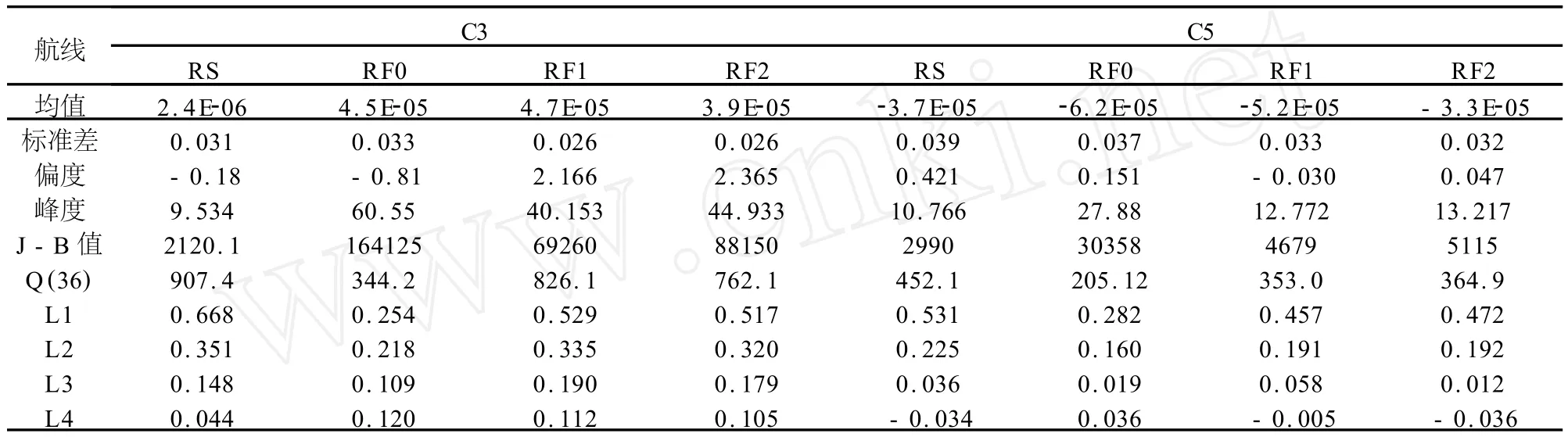
表2 即期和远期收益率的统计性描述及其自相关性

表2显示,C3的四期收益率均值都为正值,虽然很小；RS和RF0的偏度都为负,说明收益率存在巨大的下跌可能；所有峰度值均比正态分布的标准值3大许多,表明收益率分布具有尖峰厚尾特性；服从χ2分布的Jarque-Bera检验的统计量远远大于标准值5.8825,拒绝了收益率服从正态分布的假设,Q (36)检验值明显偏大,表明残差不是白噪声,存在显著异方差性。C5航线的四期收益率均为负值,尽管比较微小；偏度方面只有RF2为负值,说明其他几个市场不存在巨大下跌风险。峰度、Jarque-Bera统计量及Q(36)检验值都与C3航线的特征一致。

根据滞后4阶的自相关检验,全部序列都存在2阶自相关,C3航线各期还存在3阶自相关。这为我们在自回归(AR)和滑动平均(MA)模型中设定滞后阶数提供了依据。

(三)单位根检验

为满足GARCH模型对序列平稳性的要求,并防止时间序列的虚假回归,我们对即期和远期价格的对数化序列和收益率序列分别进行了单位根检验。检验结果说明：无论在l％、5％还是10％的显著性水平下,所有航线对数价格的ADF统计值显著大于临界值,说明对数价格序列是不平稳的,但是将对数差分以后(即收益率序列)的ADF值都小于临界值-3.43,说明所有收益率序列都是平稳的。对数序列是一阶单整序列,符合协整的前提条件。

(四)跨期相关检验

为考察残差的时效性,我们对即期收益率与远期收益率之间的跨期相关系数进行了检验。结果表明,不管是远期对即期,还是即期对远期,当期(滞后期为0)的相关系数在0.62—0.81之间,前一天(即滞后一期)相关系数在0.41—0.58之间,当期的相关性明显大于前一天的。实证中我们将分别将当天和前一天的残差项代入波动溢出方程中以考察二者的差别。

四、实证结果

我们的实证研究有五个目的：一是测试某些模型的适用性；二是分析波动的时效性,即当天还是昨天波动溢出效应更大；三是测度波动溢出的方向性,即远期对即期溢出大还是即期对远期大；四是不同远期市场波动溢出效应是否相同；五是考察C3和C5之间的差别。

(一)单变量GARCH模型

最开始我们严格按照 Hamao文章中的MA (1)-GARCH(1,1)-M作为均值方程,计算即期和远期市场间的波动溢出,发现效果不理想,主要是算不出溢出系数,见表3第3行的RF1→RS和RF2→RS,而且很多解释变量在统计上不显著。于是我们改用ARMA(2,1)模型,溢出系数都有数值,但是仍有一些在统计上不显著。最后我们试用了AR(2)模型,结果比较理想。

表3 单变量均值方程下溢出因子系数及其z检验(前一天残差)

表3显示,三种均值模型的共性很明显,第一,远期对即期市场的波动溢出小于反方向的；第二,远期市场对即期市场的溢出因子仅在0.1％—6.3％的数量级,未免太小,这与我国一些航运公司租船谈判常常参考昨天远期交易的行业做法不符；第三,个别溢出因子项在统计上不显著。

表4 AR-GARCH下溢出因子系数及z检验(前一天和当天残差)

我们用统计特性最好的AR-GARCH模型,对残差项取前一天和当天两种情况进行实验,见表4,发现结果与表3有很大的差别。残差平方采用当天的比采用前一天的溢出系数要大10倍以上,并且统计性更显著。以C3RF1→RS为例,采用当天残差所得的溢出系数为0.755,而采用前一天残差所算出的系数仅为0.0175,相差达43倍!按照常识,即期或远期市场受到另一个市场的影响只有5％的数量级确实与事实不符,75％的数量级具有更强的解释力。

然而,在如何解释当天市场间波动溢出比前一天大许多时我们遇到了困难。由于时差,亚洲即期市场开市早于欧洲远期市场,当天即期市场消息传到伦敦影响了当天远期交易可以理解。但是,即期市场也是受到当天(而不是前一天)远期市场的影响大,在时差上是不能解释的。可能的解释是,欧洲一些大型航运咨询公司既做远期也做即期,如Clarkson航运公司,不同部门之间的当天信息可能共享。这些咨询公司在替他们的客户谈判租船价格时,有条件参考当天的远期市场行情。如果是这样的话,世界干散货运输价格主要形成于欧洲而不是在拥有大部分干散货船队的亚洲。

(二)双变量EGARCH模型

我们实验了VECM和VAR两种多变量均值方程,均值方程残差平方采用前一天的,计算结果见表5。

表5 双变量均值方程下溢出因子系数及其z检验(前一天残差)

表5结果表明V ECM与VAR模型在溢出系数大小上没有太大的差别,但是,VAR模型的Z检验显著性更强,尤其是C5航线。

与上节相同,我们又对残差采用前一天和当天的进行了实验,均值方程只采用了统计显著的VAR模型,结果见表6。

表6 VAR-EGARCH下溢出因子系数及其z检验(前一天和当天残差)

首先,两条航线均是当天的溢出系数要比前一天的大,大部分都大10倍左右(C5即期对远期在两者之间的差别不大)。这进一步说明,人们不管在进行哪个市场的交易更多受到当天市场的影响而不是前一天的。其次,比较即期对远期溢出或者反方向的强度,因采用的残差时间而不同,残差为前一天时两条航线都是即期溢出大于远期溢出,残差为当天时基本上是远期溢出大于即期溢出。至于不同远期对于即期溢出效应的大小,差别不是很大。趋势也不是很一致,有时候RF1→RS最好,有时候反而可能最差。

五、结论

如上各种实证结果最重要的结论是：FFA市场对即期市场有显著的波动溢出效应,即期对远期也有波动溢出,即两个市场是双向传导的。具体细节有如下结论：

(1)就波动溢出模型的适用性而言,单变量GARCH比双变量EGARCH的统计特性好一些,主要指溢出因子系数和z检验值稍微大一些,但不是很突出。在单变量情景下,AR均值方程的统计特征最好,ARMA次之,M A-M反而最差。在双变量情景下,VAR模型比带有误差修正项的V EC模型还显著一些。看来,简单模型并一定解释力差。

(2)就残差项的时效性而言,当天残差对各个溢出方向的溢出强度远远高于前一天的。这对参与航运实体和虚拟市场的企业和投资者有重要的启示意义：只有那些能够获得当天即期和远期交易信息的公司或经纪人,才能更准确把握市场的价格走向。这对不拥有大型航运咨询公司的中国来说是很不利的。

(3)就C3和C5航线的市场效率而言,不管是什么模型,不管残差采用的是前一天还是当天的,远期对即期的溢出因子系数C5航线都比C3的大,这可以认为,C5航线的市场效率要比C3的高。个中原因可能是从C5航线进入中国的铁矿石量大,远期市场交易量也大,因而相对成熟一些。对一些欲通过FFA市场进行保值操作的企业来说,参考C5比C3市场的信息可能更有效。

(4)就实体与虚拟市场间波动溢出强度而言,在大部分情况下,即期对远期市场的波动溢出反而强于远期对即期市场的溢出,这说明FFA市场更多的依赖于即期市场,而不是引领即期市场的价格波动,这也说明了远期市场的不成熟性。

(5)就各个远期对即期波动溢出强度比较,没有明显看出哪一种远期对即期的波动溢出一直更突出。这也说明远期市场间的相关性太强,以至于买卖哪一种产品不会有太大的收益或者风险差别。

[1]Kavussanos M G,Visvikis ID.Market interactions in returns and volatilities between spot and fo rward shipping freight markets[J].Journalof Banking＆Finance,2004,(8)：2015-2049.

[2]熊正德,谢敏.金融市场间波动溢出效应理论研究与评价[J].生产力研究,2008,(1)：51-53.

[3]Hamao Y.,Masulis,R.W.Correlations in Prices Changesand Volatility Across International Stock Markets.Review s of Financial Studies,1990,3(2)：281-307.Oxford University Press.

[4]N.T.Laopodis.Asymmetric volatility spillovers in deutsche mark exchange rates[J].Journal of M ultinational Financial Management,1998,8(4)：413-430.

[5]张金清,刘庆富.中国金属期货市场与现货市场之间的波动性关系研究[J].金融研究,2006,(7)：102-112.