移动车辆荷载作用下简支箱梁动力特性的数值分析

赵晓华 张谢东 陈 湛 梅 宇

（武汉理工大学交通学院 武汉 430063）

0 引 言

所有的桥梁在移动荷载作用下都会产生强迫振动，对移动车辆荷载作用下的桥梁振动特性研究，一直是人们热心关注的问题.移动荷载模型经历了移动常量力模型、移动质量模型、滚动质量模型、移动简谐力模型、移动车辆振动系统模型［1］.人们对不同移动荷载模型作用下梁桥动力特性的数值和仿真分析，做了大量的研究［2－5］.不足的是，这些移动荷载模型并没有考虑车辆自身振动特性.本文采用更符合汽车振动特性的单自由度质量－弹簧系统模型，运用ANSYS分析软件的APDL编制命令流分析该车桥耦合模型作用下简支箱梁的动力特性，同时建立车辆滚动质量模型进行了验证，表明单自由度质量－弹簧模型更符合车辆的实际移动状态.

1 车桥振动数学模型建立

汽车振动系统简化为单自由度质量系统，对车身质量m进行受力分析，由于弹簧两端都在运动，任一瞬时弹簧的变形为x－xs，弹性恢复力为k（x－xs）.阻尼器两端也都在运动，阻尼力为），系统上作用两个激振力，一个是经过弹簧传递过来的kxs，另一个是经过阻尼器传递过来的.根据牛顿运动定律，运动微分方程为

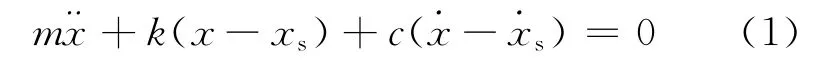
车桥振动模型如图1所示，简支箱梁抗弯刚度为EI，恒载质量均匀分布（单位长度质量为M），长度为L，不考虑剪切变形和转动惯量的影响.梁上的移动荷载是由簧上质量M1、弹簧刚度K、阻尼器C组成的体系.设梁的动挠度为y（x，t），簧上质量的动位移为y（t），簧下车轮（质量不计）假定沿梁长移动而不脱离梁体.

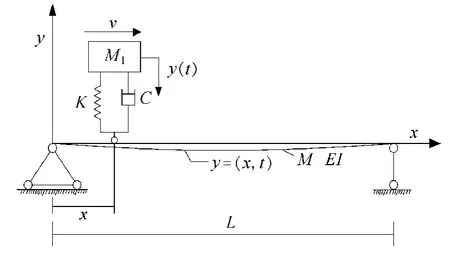
图1 单自由度质量弹簧模型作用下的简支箱梁

简支梁在外荷载p（x，t）作用下的振动方程［6－7］为

则对于图1所示的车桥系统，其振动方程为

利用分离变量法，令

式中：φn（x）为简支梁第n阶模态（振型）函数；qn（t）为t时刻第n阶模态响应.则

引入简支梁的振型φn（x）＝，且不考虑简支梁的阻尼系数，将式（5）、（6）代入式（3）、（4）中，建立车 －桥耦合系统竖向振动方程为［8－12］

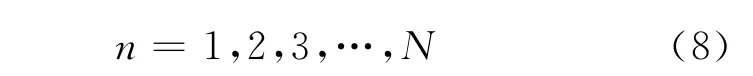
2 车桥耦合振动模型动力特性分析

2.1 车桥耦合模型建立

汽车质量M＝19 200kg，弹性刚度K＝6×105N／M，阻尼C＝36 000N·s／m.简支梁桥全长L＝32m，弹性模量E＝210GPa，泊松比μ＝0.2，密度ρ＝2 400kg／m3，面积S＝3.16m2，高度H＝1.7m.选取图1所示单自由度质量弹簧车桥模型及参数，利用ANSYS软件及APDL语言建立简支箱梁桥的几何模型.其中移动汽车荷载模型由mass21和combin14单元模拟，简支箱梁桥模型用beam3单元建立二维几何模型，分析移动速度36，72，120km／h作用下，简支梁桥的动态响应情况.

2.2 车桥耦合振动变形分析

将汽车简化为车身作垂直振动的单自由度质量弹簧模型，建立单自由度质量－弹簧－桥梁耦合模型进行计算，同时建立了滚动质量有限元模型进行验算.图2给出了移动荷载作用下简支梁桥结构的变形情况.

图2 车桥耦合模型整体变形图

图2表明简支梁桥在移动荷载作用下，跨中节点的挠度最大，这说明对移动荷载作用下简支梁最大挠度的研究只要对跨中节点位移的规律进行研究即可；本例的跨中位移值较小，图2中桥梁跨中的挠度变化经过了比例放大，这是由于桥梁的质量、刚度较大，而引起跨中挠度变化相对较小造成的.

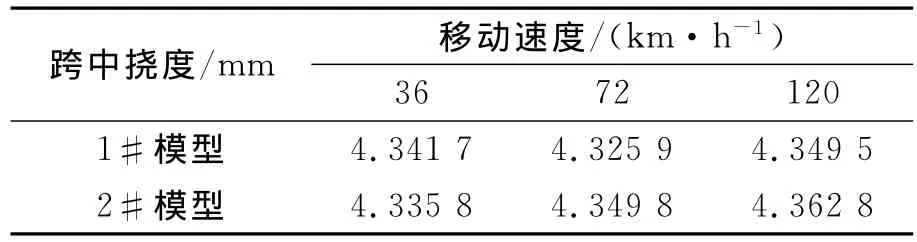
表1 不同移动速度下桥梁最大位移值

由表1的计算结果可知，简支梁的跨中最大挠度随着速度的增大而有增大的趋势，且2＃模型的跨中挠度略大，约大0.3%～0.5%，由于2＃模型没有考虑车辆自身的减震性能，与桥面刚性接触，跨中挠度较1＃模型计算结果稍大，表明弹簧－质量车桥耦合模型更符合车辆实际行驶状况，且计算结果与弹簧质量模型相差很小.

当车速从36km／h增大到120km／h时，无论是1＃模型还是2＃模型，其动力响应受车速影响，跨中挠度增大.根据计算，汽车刚驶离桥尾时，挠度最大值出现在跨中节点之后位置，而汽车离开桥尾一段时间后，挠度最大值才出现在跨中节点处，且前者的挠度值略微偏大，说明简支梁桥最大动位并不是发生在移动荷载位于跨中时，而是具有一定的时间滞后性，并且移动荷载引起的振动与桥梁结构模态合并，动位移经叠加之后趋于稳定.

2.3 车桥耦合振动跨中动响应分析

图3～图5是弹簧－质量车桥耦合模型中，移动速度分别为36，72，120km／h作用下的桥梁跨中动挠度时程曲线，从图中可以看出，当移动车辆荷载以不同的速度通过桥梁后，桥梁跨中挠度呈现出具有一定频率的类正弦波曲线，且在低速行驶时，跨中挠度振荡更加明显.由此可见，车辆以不同的速度移动时，桥梁跨中挠度的变化并非与速度成简单线形关系，而是随时程振动叠加.这样的规律可以从车桥共振的角度做出解释.车辆经过桥梁时，随着车速的改变，车辆对桥梁的加载频率发生变化，在某个车速段下，其加载频率与梁的某阶自振频率接近，使得结构的反应达到极大.

图3 36km／h作用下跨中动挠度变化

表2的计算结果表明，随着移动速度的增大，桥梁跨中动速度达到最大值所需时间越短，且最大值呈减小趋势.桥梁跨中最大动速度值并非车辆移动至跨中位置而产生，而是随着速度的增大，跨中动速度达到最大值所需的行驶距离越长.表2计算结果还可以看出，跨中动加速度均方根值随速度增大而减小，36km／h时加速度均方根值为0.009 7m／s2，比72km／h的加速度均方根大54%，而72km／h的加速度均方根比120km／h的均方根大大约24%，表明车辆低速行驶时，应考虑桥梁跨中的动加速度情况.这些规律主要是由于行驶速度的增大，车辆与桥梁接触的作用时间较短，桥梁体系受移动荷载影响程度较小所致.

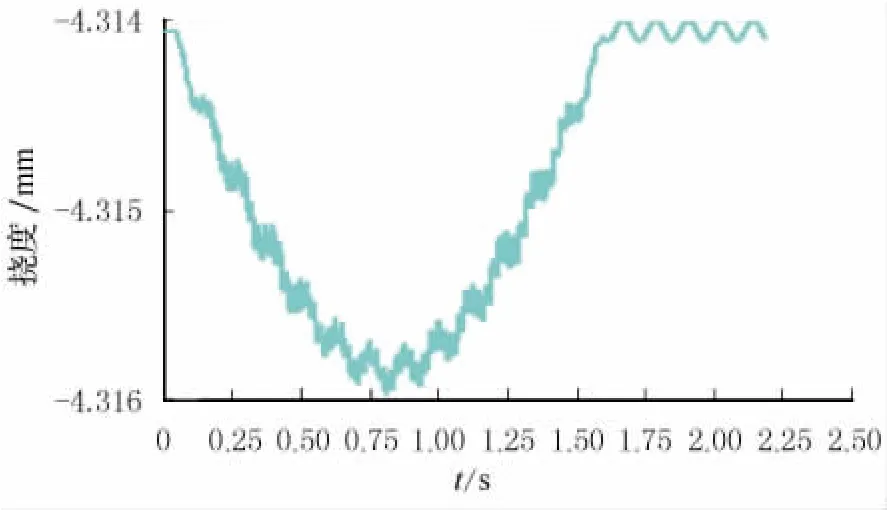
图4 72km／h作用下跨中动挠度变化

图5 120km／h作用下跨中动挠度变化

表2 不同速度下桥梁跨中动响应变化

3 结 论

1）通过单自由度质量－弹簧和滚动质量车桥耦合模型的对比计算，验证了单自由度质量弹簧车桥耦合模型的合理性和可行性，该车桥耦合模型能反映实际车桥耦合振动系统的动力特性，更适宜模拟实际车辆的运行状态.

2）计算结果表明：不同速度下，简支薄壁箱梁的跨中变形最显著，跨中位移随时程呈类正弦波曲线变化；随速度的增大，跨中挠度最大值略有增加，跨中动加速度的均方根值呈减小趋势；跨中动速度达到最大值所需时间变短，移动荷载的行驶距离变长.

3）本文的计算结果对进一步了解实际简支薄壁箱梁桥在不同行驶速度下的动力特性规律和机理有一定的参考价值，为类似简支薄壁箱梁桥的设计和分析提供重要的依据和理论参考.

［1］盛国刚，李传习，赵 冰.多个移动车辆作用下简支梁的动力响应分析［J］.工程力学，2006，23（12）：154－158.

［2］丁 涛，殷志祥.基于ANSYS的桥梁强迫振动分析［J］.辽宁工程技术大学学报，2005，24（增刊）：87－89.

［3］Cai C S，Chen S R.Framework of vehicle－bridge－wind Dynamic Analysis［J］.Journal of Wind Engineering and Industrial Aerodynamics，2004，92（7／8）：579－608.

［4］赵 青.移动车辆荷载作用下梁桥的冲击系数研究［J］.安徽建筑工业学院学报：自然科学版，2004，12（6）：31－33.

［5］桂水荣，陈水生，许士强.移动荷载下简支梁桥3种车桥耦合模型研究［J］.华东交通大学学报，2007，24（4）：35－38.

［6］宋一凡.公路桥梁动力学［M］.北京：人民交通出版社，2000.

［7］李国豪.桥梁结构稳定与振动［M］.北京：中国铁道出版社，1996.

［8］Yang Yeongbin，Yau Jongdar.Vehicle－bridge interaction element for dynamic analysis［J］.Journal of Structural Engineering，1997，23（11）：1 521－1 518.

［9］瞿伟廉，刘 嘉.万州长江大桥车桥耦合振动的研究［J］.华中科技大学学报：城市科学版，2004，21（3）：1－4.

［10］ Memory T J，Thambiratnam D P，Brameld G H.Free vibration analysis of bridges［J］.Engineering Structures，1995，17（10）：705－713.

［11］耿 波，张谢东，沈成武，向木生.大跨径连续箱梁桥静载试验研究［J］.武汉理工大学学报：交通科学与工程版，2004，28（5）：755－758.

［12］肖新标，沈火明.移动荷载速度对简支梁动态响应的影响［J］.西南交通大学学报，2002，37（增刊）：35－38.