组分梯度膜的有效介电常数的推导

缪秀平

（镇江高等专科学校 化工系，江苏 镇江 212003）

0 引言

利用边值关系求介质内的电场和束缚电荷的分布是电动力学教学中的基本问题之一［1-2］，其研究的介质均为各向同性。随着科学的发展，在实际应用中常常会出现各向异性的复合材料，如磁光子晶体［3-4］、功能梯度材料［5］等。这些各向异性的复合材料性能特异、材料设计思想新颖，具有重要的应用背景，各国科研工作者高度重视其研究。笔者主要从边值关系出发，研究具有组分梯度的复合体系的有效介电常数。

1 理论模型

主要研究图1所示的组分梯度膜。组分梯度膜由具有各向异性金属颗粒分布在各向同性的基质中，且金属颗粒的体积分数沿垂直于梯度膜的z方向变化，沿z方向的薄膜厚度为W。设金属颗粒的介电常数为1，基质的介电常数为εh=ε0I，I为单位张量。假设金属颗粒的大小满足有效媒质理论的条件，设金属颗粒为类球状，且对称轴平行于外加磁场方向（设为z轴方向），则该金属颗粒的介电常数1可设为［6-7］

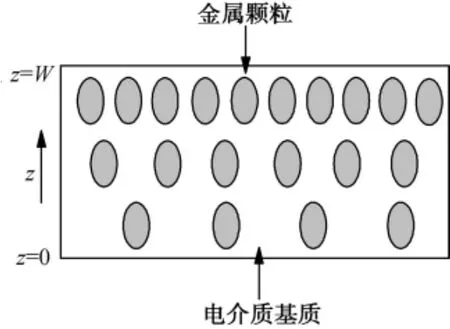
图1 组分梯度膜示意图

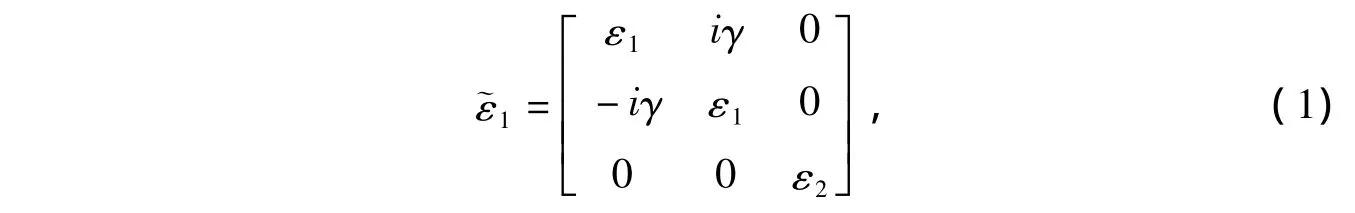
式（1）中，εi（i=1，2），γ分别为介电常数1的对角元素和非对角元素。

2 理论推导

选取组合梯度膜任意一个位置的z层作为研究对象，该z层可近似看成由介电常数为1的金属颗粒分布在介电常数为εh=ε0I的基质中而组成的复合介质，其中金属颗粒的体积分数为p（z），基质的体积分数为1-p（z）。该z层的等效介电常数可运用文献［7］中的有效媒质理论进行研究。设该z层的等效介电常数为

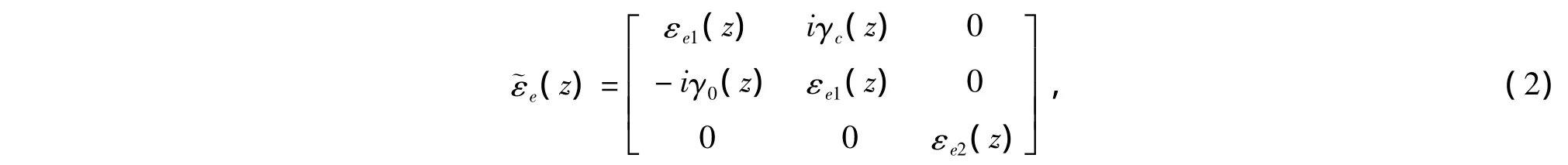
式（2）中，非对角元γe（z）和对角元εe1（z），εe2（z）均为z的函数。根据有效媒质理论，设整个梯度膜的有效介电常数为

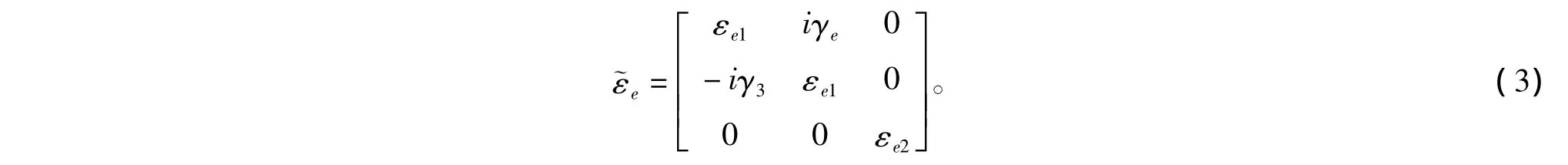
取复合梯度膜任意相邻的两层为研究对象。由于位置不同，金属颗粒的体积分数也不同，由式（2）可知，这两层的等效介电常数也不同，为推算方便，将其中一层视为介质a，介电常数为a（za），厚度为da，另一层视为介质b，介电常数为˜b（zb），厚度为db，如图2所示。

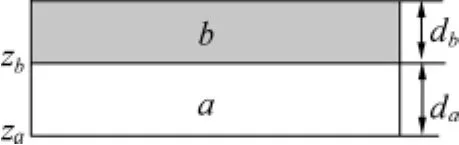
图2 任意相邻两层介质示意图

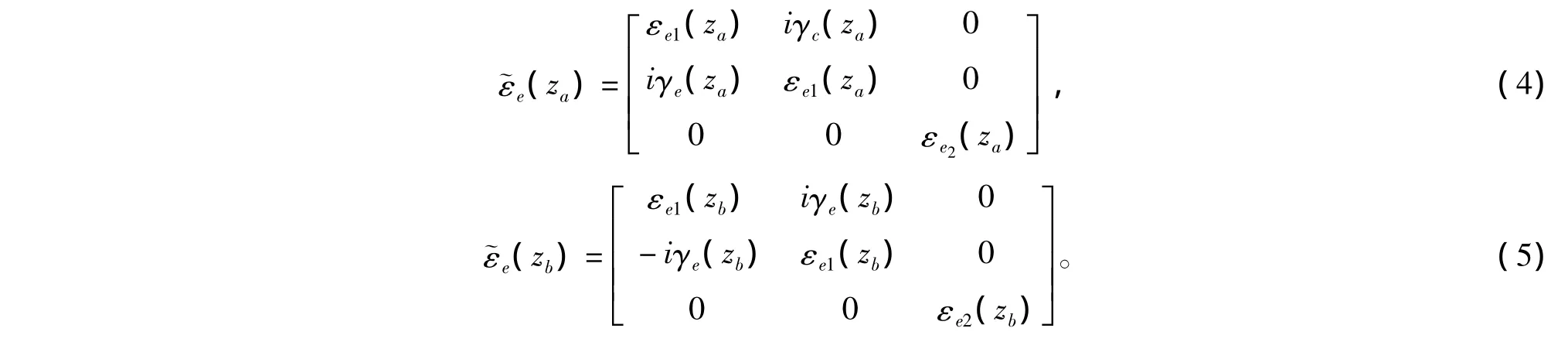
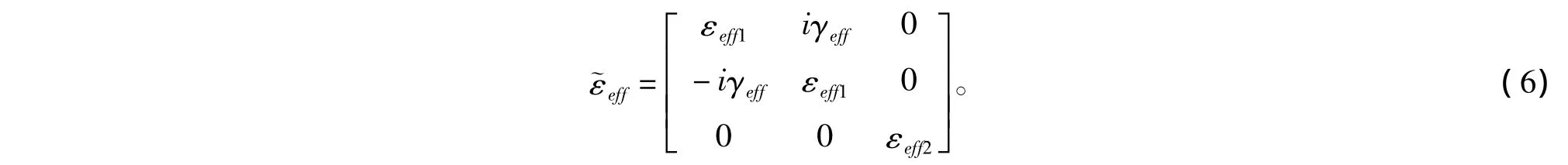
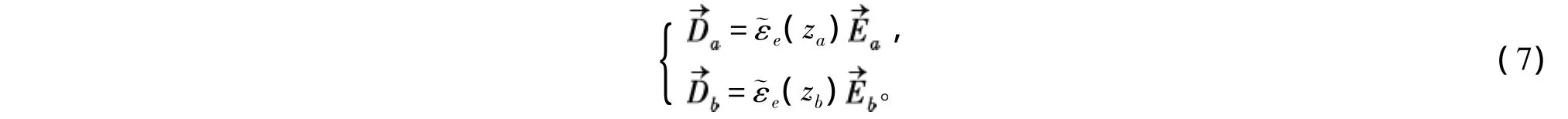
根据边值关系

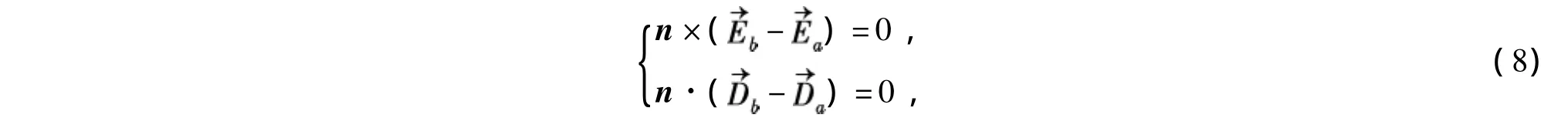
得

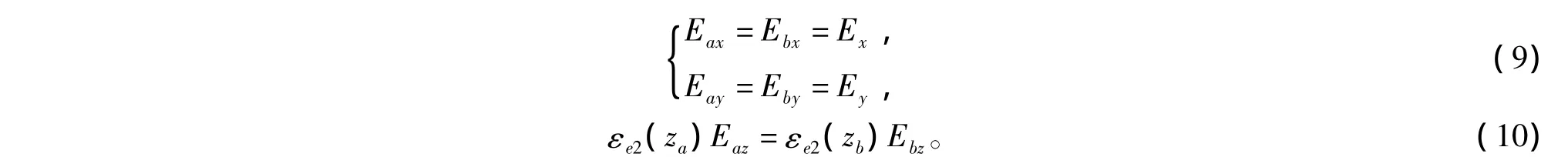
由平均场理论有

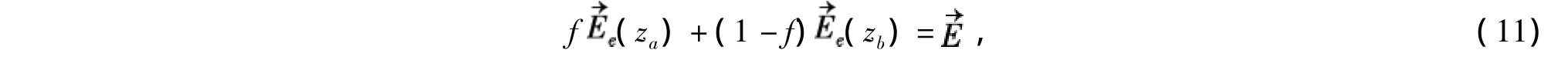
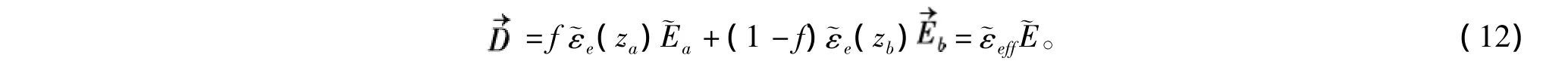
解由式（10），式（11）组成的方程组得

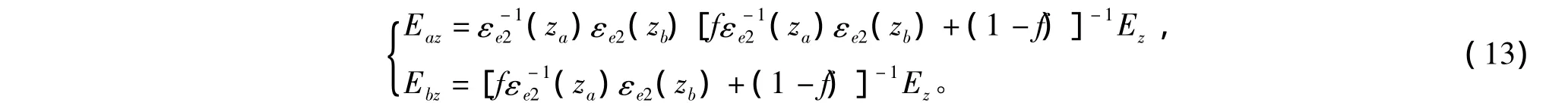
由式（9），式（13）可得介质a，b中的感应电场

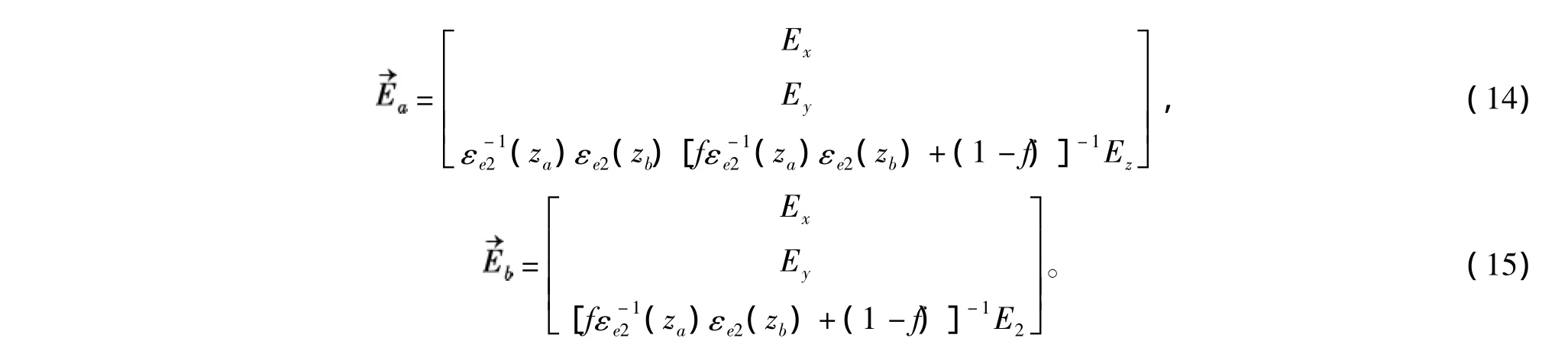
将式（14），式（15）代入式（12）得

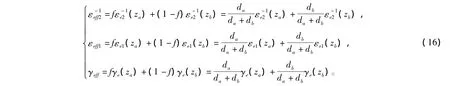
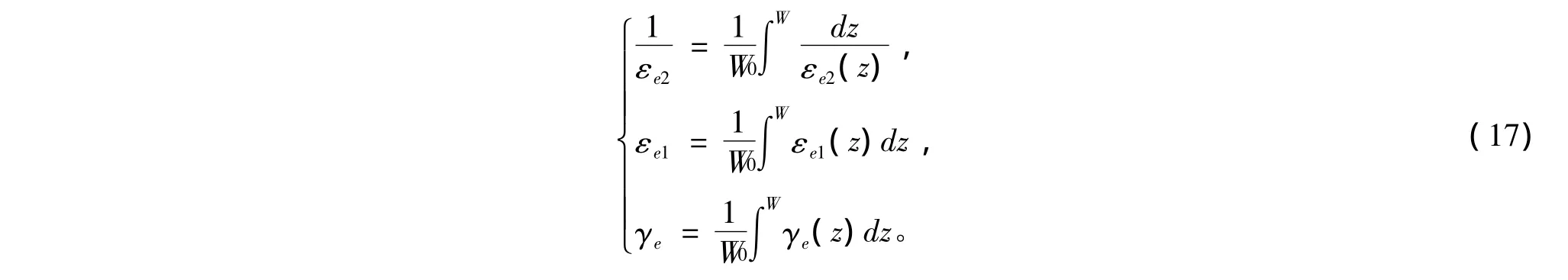
3 结论

笔者从静电场的边界条件出发，利用平均场理论和有效媒质理论推导出组分梯度膜的有效介电常数的表达式，为进一步研究具有组分梯度的复合体系的其他物理性质提供了一定的理论基础。

［1］郭硕鸿.电动力学［M］.北京：高等教育出版社，1997.

［2］赵凯华，陈熙谋.电磁学［M］.北京：高等教育出版社，1985.

［3］JOHN S S.Localization of photons in certain disordered dielectric super lattices［J］.Phys Rev Lett，1987，58（23）：2486-2489.

［4］YABLONOVITCH E.Inhibited spontaneous emission in solid-state physics and electronics［J］.Phys Rev Lett，1987，58（20）：2059-2061.

［5］新野正之，平井敏雄，渡边龙三.倾斜机能材料：宇宙机用超耐热材料应用［J］.日本复合材料学会志，1987，13（6）：257-264.

［6］HUI P M，STROUD D.Theory of faraday rotation by dilute suspensions of small particles［J］.Appl Phys Lett，1987，50（15）：950-952.

［7］XIA T K，HUI P M，STROUD D.Theory of faraday rotation in granular magnetic materials［J］.App1 Phys，1990，67（6）：2736-2741.